纯粹是为了节省篇目所以把这俩合在一起了
高维前缀和(sosDP)
不是很懂我为什么要在FWT之后学这个东西
子集和DP Sum over Subsets dynamic programming 一般用来解决这种东西:
直接枚举子集是 (mathcal{O}(3^n)) 的,用这个东西做到 (mathcal{O}(ncdot 2^n)) .
思路&实现
先考虑维度较低的前缀和。众所周知,二维前缀和就是四个矩形容斥一下。但是还有一种写法是对每一个维度分别求前缀和:
for ( int i=1; i<=n; i++ )
for ( int j=1; j<=n; j++ )
a[i][j]+=a[i-1][j];
for ( int i=1; i<=n; i++ )
for ( int j=1; j<=n; j++ )
a[i][j]+=a[i][j-1];
如果维度上升到三维甚至更多,容斥会变得极其不可做,但是这种逐维求和的方式还是可行的。
高维前缀和利用的其实就是这种按位的思想,加上一个DP。
以上面的子集问题为例,设 (dp[i][S]) 表示状态为 (S) ,二进制最后 (i) 位和 (S) 不同的子集的信息之和。
对于这种子集关系,放一张 剽来的图 :
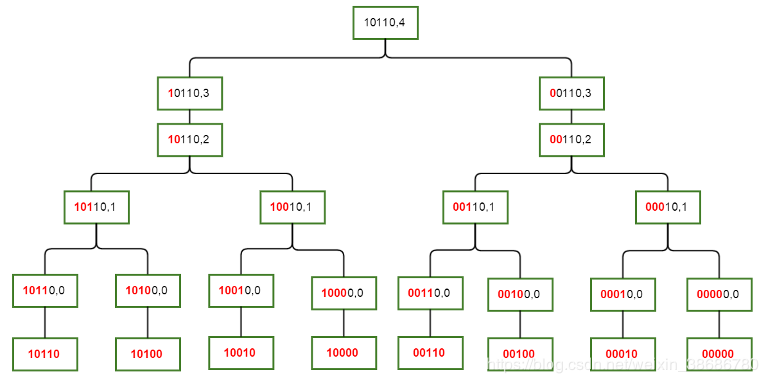
容易发现,我们每次只需要统计枚举的当前位为 (0/1) 的、上一层的子集答案,并且在当前位为 (0) 的时候只需要统计为 (0) 的情况。写成代码就是(这里把第一维滚掉了w)
for ( int i=0; i<(1<<n); i++ ) f[i]=a[i];
for ( int i=0; i<n; i++ )
for ( int S=0; S<(1<<n); S++ )
if ( S&(1<<i) ) f[S]+=f[S^(1<<i)];
超集:如果 (S_2subseteq S_1) ,那么 (S_1) 是 (S_2) 的超集。
sosDP 同样可以用来解决超集求和问题,方法是几乎相同的,可以理解为把子集问题中所有的 (01) 反转。
for ( int i=0; i<(1<<n); i++ ) f[i]=a[i];
for ( int i=0; i<n; i++ )
for ( int S=0; S<(1<<n); S++ )
if ( !(S&(1<<i)) ) f[S]+=f[S^(1<<i)];
注:更一般的情况下,高维前缀和中这个 += 是将两个答案合并,即 f[S]=Merge(f[S],f[S^(1<<i)]) .
习题
Or Plus Max
给定一个长度为 (2^n) 的序列 (a) ,对于 (1leq kleq 2^n-1) ,求 (max{a[i]+a[j]},forall i|jleq k) ,(k) 取遍 (1sim 2^n-1) 。
(forall i|jleq k) 这个条件可以转化为:求出 (i|j=k) 的答案,然后前缀 (max) 。而对于 (i|j=k) ,又可以转化为 (i|jsubseteq k) ,因为如果或出来是个真子集只会让答案更小。到了这一步,其实就是求 (k) 所有子集中 (a[i]) 的最大值和次大值,然后合并答案即可。
//Author: RingweEH
void bmax( int &a,int b ) { a=(a>b) ? a : b; }
const int N=19,INF=0x3f3f3f3f;
struct Node
{
int mx1,mx2;
Node ( int _mx1=-INF,int _mx2=-INF ) : mx1(_mx1),mx2(_mx2) {}
}f[1<<N];
int a[1<<N],n;
Node Merge( Node t1,Node t2 )
{
Node res=t1;
if ( t2.mx1>res.mx1 ) res.mx2=res.mx1,res.mx1=t2.mx1,bmax(res.mx2,t2.mx2);
else bmax( res.mx2,t2.mx1 );
return res;
}
int main()
{
n=read(); int m=1<<n;
for ( int i=0; i<m; i++ ) a[i]=read();
for ( int i=0; i<m; i++ ) f[i]=Node(a[i]);
for ( int i=0; i<n; i++ )
for ( int S=0; S<m; S++ )
if ( S&(1<<i) ) f[S]=Merge(f[S],f[S^(1<<i)]);
int ans=0;
for ( int i=1; i<m; i++ )
bmax( ans,f[i].mx1+f[i].mx2 ),printf("%d
",ans );
return 0;
}
Bits And Pieces
给定一个长度为 (n) 的序列 (a) ,求对于所有满足 (i<j<k) 的三元组 ((i,j,k)) ,(max{a_i|(a_j&a_k)}) .
某一个数 (x) 出现两次及以上就能被 (&) 出来了,所以可以枚举 (a[i]) 然后统计对应的 (a[j]&a[k]) ,再把 (a[i]) 统计进去,顺带满足大小关系。
//Author: RingweEH
void Add( int x,int p )
{
if ( cnt[x]>=2 ) return;
if ( p==-1 ) { cnt[x]++; return; }
Add( x,p-1 );
if ( x&(1<<p) ) Add( x^(1<<p),p-1 );
}
int Get( int x )
{
int res=0;
for ( int i=20; i>=0; i-- )
if ( !(x&(1<<i)) && cnt[res|(1<<i)]>=2 ) res|=(1<<i);
return res|x;
}
int main()
{
n=read();
for ( int i=1; i<=n; i++ ) a[i]=read();
int ans=0;
for ( int i=n; i; i-- )
{
if ( i<=n-2 ) bmax( ans,Get(a[i]) );
Add( a[i],20 );
}
printf("%d
",ans );
return 0;
}
Compatible Numbers
问数组中的每个数 (a[i]) 是否可以在数组里面找到 (a[j]&a[i]=0) ,输出 (a[j]) 或 -1 .
也就是找 (a[i]) 取反之后的子集。
//Author: RingweEH
int main()
{
memset( dp,-1,sizeof(dp) );
n=read();
for ( int i=1; i<=n; i++ ) a[i]=read(),dp[a[i]]=a[i];
int lim=(1<<22);
for ( int i=0; i<=22; i++ )
for ( int S=0; S<lim; S++ )
if ( dp[S]==-1 && (S>>i&1) ) dp[S]=dp[S^(1<<i)];
for ( int i=1; i<=n; i++ ) printf("%d ",dp[(lim-1)^a[i]] );
return 0;
}
动态DP(DDP)
前置芝士:
- 矩阵乘法加速递推
- 一定的数据结构基础(线段树、树剖、LCT……)
广义矩阵乘法
DDP 的基本思想是把DP转移式拆成矩阵乘法,然后再用数据结构维护。很多DP式里面都有 (max) ,无法用一般的加法乘法表达,所以我们需要对矩阵乘法进行魔改。
矩阵乘法的结合律的成立只依赖于乘法对加法有分配率,(acdot(b+c)=ab+ac) ,而加法对 (minmax) 也有分配率,(a+max(b,c)=max(a+b,a+c)) ,所以可以重定义矩阵乘法:(C[i][j]=max_k{A[i][k]+B[k][j]}) ,发现这个新的矩乘很像 Floyd ,而 Floyd 的原理又是DP……所以?
引例 - SP1716
(n) 个数,(q) 次操作。
0 x y(a[x]) 修改为 (y)1 l r询问 ([l,r]) 最大子段和。
首先列出最大子段和的DP式:设 (f[i]) 表示以 (a[i]) 结尾的最大子段和,(g[i]) 表示 ([1,i]) 的最大子段和。
把这玩意儿改写成矩阵乘法:
线段树维护区间矩阵乘积即可。
//Author: RingweEH
#define ls pos<<1
#define rs pos<<1|1
const int N=5e4+10,INF=INT_MAX>>2;
struct Matrix
{
int mat[3][3];
Matrix(){for(int i=0;i<=2;i++)for(int j=0;j<=2;j++)mat[i][j]=-INF;}
}tr[N<<2];
int a[N],n,q;
Matrix operator * ( const Matrix &A,const Matrix &B )
{
Matrix res;
for ( int k=0; k<=2; k++ )
for ( int i=0; i<=2; i++ )
for ( int j=0; j<=2; j++ )
bmax( res.mat[i][j],A.mat[i][k]+B.mat[k][j] );
return res;
}
void Pushup( int pos ) { tr[pos]=tr[ls]*tr[rs]; }
void Build( int pos,int l,int r )
{
if ( l==r )
{
tr[pos].mat[0][0]=tr[pos].mat[0][2]=tr[pos].mat[1][0]=tr[pos].mat[1][2]=a[l];
tr[pos].mat[1][1]=tr[pos].mat[2][2]=0; return;
}
int mid=(l+r)>>1;
Build(ls,l,mid); Build(rs,mid+1,r); Pushup(pos);
}
void Modify( int pos,int l,int r,int x,int val )
{
if ( l==r ) { tr[pos].mat[0][0]=tr[pos].mat[0][2]=tr[pos].mat[1][0]=tr[pos].mat[1][2]=val; return; }
int mid=(l+r)>>1;
(x<=mid) ? Modify(ls,l,mid,x,val) : Modify(rs,mid+1,r,x,val);
Pushup(pos);
}
Matrix Query( int pos,int L,int R,int l,int r )
{
if ( l<=L && R<=r ) return tr[pos];
int mid=(L+R)>>1;
if ( l<=mid && r>mid ) return Query(ls,L,mid,l,r)*Query(rs,mid+1,R,l,r);
return ( l<=mid ) ? Query(ls,L,mid,l,r) : Query(rs,mid+1,R,l,r);
}
int main()
{
n=read();
for ( int i=1; i<=n; i++ ) a[i]=read();
q=read();
Build(1,1,n);
while ( q-- )
{
int opt=read(),x=read(),y=read();
if ( opt )
{
if ( x>y ) swap( x,y );
Matrix res=Query( 1,1,n,x,y );
printf("%d
",max(res.mat[1][0],res.mat[1][2]) );
}
else a[x]=y,Modify(1,1,n,x,y);
}
return 0;
}
P4719 树的最大权独立集
给定一棵 (n) 点树,(m) 次单点修改点权操作,每次操作之后求最大权独立集权值大小。
先不带修改找式子。显然是
然后,考虑要套什么数据结构。由于这里复杂度要求是 (mathcal{O(nlog n)}) ,所以不难想到用重链剖分。然而我貌似有点忘了
树剖复习。
其实就是按照子树大小划分轻重儿子/边,然后轻重链取极长,重节点优先遍历出来的DFS序中重链、子树都是连续的。而且有重要性质:任何一个节点到根节点的路径中,包含不超过 (log n) 条重链。
找重儿子和DFS序可以两遍完成。后面就是在DFS序上维护东西了,没什么好说的。
为了能树剖,要把DP式子稍微修改一下:令 (g[u][0]) 表示 (u) 所有轻儿子,随意取的最大权独立集;(g[u][1]) 表示 (u) 所有轻儿子不取自己的最大值,加上 (u) 本身的权值。转移方程就可以把求和去掉,变成(这里 (v) 是重儿子)
然后就要把它写成矩阵:
为了节省空间把一些常见结构体省略了……
//Author: RingweEH
void bmax( int &a,int b ) { a=(a>b) ? a : b; }
#define ls pos<<1
#define rs pos<<1|1
const int N=1e5+1,M=2e5+1,NM=4e5+1,INF=0x3f3f3f3f;
int tot,head[N],n,m,tim,f[N][2];
int a[N],fa[N],siz[N],dep[N],dfn[N],id[N];
int wson[N],top[N],ed[N];
struct Matrix
{
int mat[2][2];
Matrix(){memset(mat,-0x3f,sizeof(mat));}
}val[N];
Matrix operator * ( Matrix A,Matrix B )
struct Edge { int to,nxt; }e[M];
void Adde( int u,int v )
struct SegmentTree { int le[NM],ri[NM]; Matrix tr[NM]; }Tr;
void DFS1( int u )
{
siz[u]=1;
for ( int i=head[u]; i; i=e[i].nxt )
{
int v=e[i].to;
if ( v==fa[u] ) continue;
fa[v]=u; dep[v]=dep[u]+1; DFS1(v);
siz[u]+=siz[v];
if ( siz[v]>siz[wson[u]] ) wson[u]=v;
}
}
void DFS2( int u,int lin )
{
id[u]=++tim; dfn[tim]=u; top[u]=lin; bmax(ed[lin],tim);
f[u][0]=0; f[u][1]=a[u];
val[u].mat[0][0]=val[u].mat[0][1]=0; val[u].mat[1][0]=a[u];
if ( wson[u]^0 )
{
DFS2(wson[u],lin);
f[u][0]+=max(f[wson[u]][0],f[wson[u]][1] ); f[u][1]+=f[wson[u]][0];
}
for ( int i=head[u]; i; i=e[i].nxt )
{
int v=e[i].to;
if ( v==fa[u] || v==wson[u] ) continue;
DFS2(v,v);
f[u][0]+=max(f[v][0],f[v][1]); f[u][1]+=f[v][0];
val[u].mat[0][1]=val[u].mat[0][0]+=max(f[v][0],f[v][1]);
val[u].mat[1][0]+=f[v][0];
}
}
void Update( int x,int y )
{
val[x].mat[1][0]+=y-a[x]; a[x]=y;
Matrix pre,las;
while ( x^0 )
{
pre=Tr.Query(1,id[top[x]],ed[top[x]]);
Tr.Modify(1,id[x]);
las=Tr.Query(1,id[top[x]],ed[top[x]]);
x=fa[top[x]];
val[x].mat[0][0]+=max(las.mat[0][0],las.mat[1][0])-max(pre.mat[0][0],pre.mat[1][0]);
val[x].mat[0][1]=val[x].mat[0][0]; val[x].mat[1][0]+=las.mat[0][0]-pre.mat[0][0];
}
}
int main()
{
n=read(); m=read();
for ( int i=1; i<=n; i++ ) a[i]=read();
for ( int i=1,u,v; i<n; i++ ) u=read(),v=read(),Adde(u,v),Adde(v,u);
DFS1(1); DFS2(1,1);
Tr.Build(1,1,n); Matrix ans;
for ( int i=1,x,y; i<=m; i++ )
{
x=read(); y=read();
Update(x,y); ans=Tr.Query(1,id[1],ed[1]);
printf("%d
",max(ans.mat[0][0],ans.mat[1][0]) );
}
return 0;
}