\(0.\) 树状数组
树状数组 \((Binary\ \ Indexed\ \ Trees)\) 是一种可以支持单点修改,较快维护前缀和的数据结构。他的实现方式是用一个数组维护一个“树状”的结构(如下图所示),记录一些区间的区间和,实现快速计算前缀和。
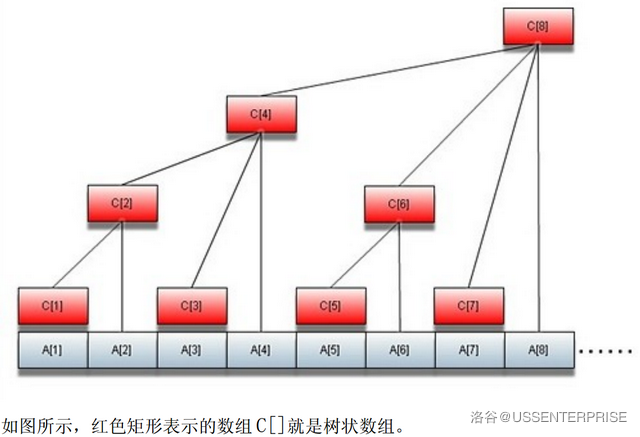
\(1.\) 前置知识
前缀和
能看到这里的同学应该已经对前缀和不陌生了。本片博客就不再赘述
\(lowbit\)操作
\(lowbit\) 操作是表达二进制下最低的 \(1\) 所表达的数值。树状数组利用了这个操作。当我们定义树状数组\(c\)时,\(c[i]=\sum_{j=i-lowbit(i)}^ia[j]\)。
\(lowbit\)实现方式:
inline int lowbit(int x){ return x&(-x); }
定义宏也可
\(2.\) 单点修改
首先我们考虑对第\(i\)个数进行修改。理所应当我们应该修改所有管控第\(i\)个数的所有节点。我们可以观察到,第[i]个数所对应的父亲节点就是\(i+lowbit(i)\)。所以每次我们只需向上跳,直到\(i>n\)即可完成所有修改
inline void upd(int x,int k){
for(;x<=n;x+=lowbit(x))
c[x]+=k;
}
\(3.\)查询前缀和
我们知道,\(lowbit(i)\)代表\(c[i]\)包含自身向前覆盖的区域大小,所以我们能得出\(\sum_1^ia[i]\)就是\(c[i]+c[i-lowbit(i)]+...\)
inline int query(int x){
rg int res=0;
for(;x>0;x-=lowbit(x)) res+=c[x];
return res;
}
(注:洛谷P3374)
\(4.\)树状数组变形
区间修改单点查询
我们考虑对\(a[\ ]\)数组建立一个差分数组\(d[\ ]\)。可以发现\(a[i]=\sum_{j=1}^id[j]\)。于是这个问题就变成了一个树状数组板子题对于差分数组建立树状数组的题目。
不会运用差分维护区间修改单点查询的同学请查看我的另一篇博客(传送门 博客未完待续中)或者百度“差分 博客园”
#include<bits/stdc++.h>
using namespace std;
namespace Enterprise{
#define rg register
#define ll long long
#define ull unsigned long long
inline int read(){
rg int s=0,f=0;
rg char ch=getchar();
while(not isdigit(ch)) f|=(ch=='-'),ch=getchar();
while(isdigit(ch)) s=(s<<1)+(s<<3)+(ch^48),ch=getchar();
return f?-s:s;
}
const int N=500015;
int a[N],d[N],c[N],n,m;
#define lowbit(x) (x&(-x))
inline void upd(int x,int k){
for(;x<=n;x+=lowbit(x)) c[x]+=k;
}
inline int query(int x){
rg int res=0;
for(;x>0;x-=lowbit(x)) res+=c[x];
return res;
}
inline void main(){
n=read(),m=read();
for(rg int i=1;i<=n;i++){
a[i]=read();
d[i]=a[i]-a[i-1];
upd(i,d[i]);
}
for(rg int i=1;i<=m;i++){
rg int opt=read();
if(opt==1){
rg int x=read(),y=read(),k=read();
upd(x,k);
upd(y+1,-k);
}else{
rg int x=read();
printf("%d\n",query(x));
}
}
}
}
signed main(){
Enterprise::main();
return 0;
}
区间修改区间查询
区间修改查询是一种线段树写起来比较方便也可用树状数组维护的问题类型,而且应该是出现频率最高的一种。
作者暂时不在里讲解做法,有兴趣的同学请自行百度
\(5.\) \(Last\ to\ tell\)
树状数组的题线段树均可解决
我树状数组板子题线段树过的