题意：
给出一个边长为a的正方形，其左下角坐标为（0，0），右上角坐标为（a，a）。
此外，再给出一个边长为b的小正方形，以及它的左下角坐标（x，y），其右上角。
坐标为（x+b，y+b），并且保证小正方形一定在大正方形内（有可能会与大正方形的边重合，但不会超出大正方形）。
问是否存在一个在顶点都在大正方形边上的三角形，满足三角形一条边在包含小正方形的一条边（小正方形的一条边在三角形的一条边上），并且三角形包含小正方形（小正方形在三角形内部，正方形的顶点或者边可以与三角形边重合）。
若存在，输出‘yes’，否则输出‘no'。
输入：
输入的第一行包含一个整数T，代表T组测试数据。接下来T行，每行给出四个数字a，b，x，y
分别代表大正方形的边长，小正方形的边长以及小正方形左下角的坐标。
输入保证
T<=100000；
1<=b<=a<=10000；
0<=x,y<=a-b
输出：
对于每一组测试数据，输出一行。’yes'代表存在该三角形，'no'代表不存在。
样例输入：
4
4 1 1 2
3 1 1 2
3 1 0 0
3 2 1 1
样例输出：
yes
yes
yes
no
解释说明：
样例1: 接下来的图片展示了一种可能的构造三角形的方案：
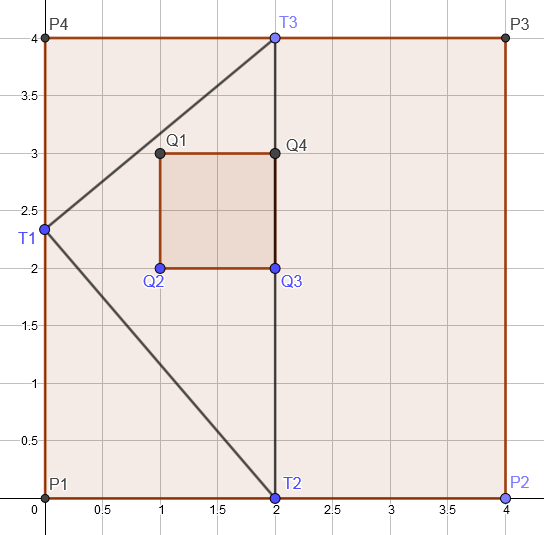
正方形A是P1 P2 P3 P4, 正方形B 是Q1 Q2 Q3 Q4以及构造的三角形T是T1 T2 T3.
样例2: 接下来的图片展示了一种可能的构造三角形的方案：
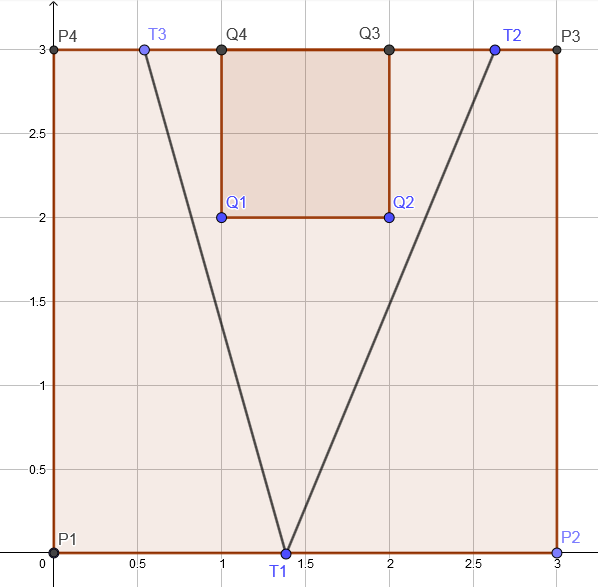
正方形A是P1 P2 P3 P4, 正方形B 是Q1 Q2 Q3 Q4以及构造的三角形T是T1 T2 T3.
（这里不得不提一句Codechef的中文翻译是真的很垃圾，之后为什么VJ不能把图片爬下来？）
一开始看到这个题目时，我是直接想当小正方形的面积大于正方形面积的1/4时直接判断no，之后其他都应该是yes才对。
之后就莽了一发，WA声一片。还是我想得太简单了。以下的情况就是我上面思路的反例。
（此时的小正方形面积大正方形的1/4但是是无法构造三角形的）
所以我们就能很自然地想到能否构造三角形的应该是取决于正方形的位置以及其面积的。那么我们就从一般的三角形出发。
首先我们明确一点是由于三角形是三条边，而正方形是四个点，那么能让正方形内嵌在三角形的最小三角形，必然是长这样的。
具体的证明应该是设参解方程，但是这里就不再赘述。
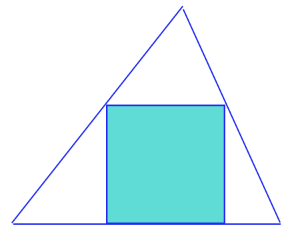
（即三角形有一条边在正边形上，又因为小正方形与大正方形相似，所以三角形必然有一条边平行于大正方形）
那么我们首先在大正方形内任意取一个小正方形：
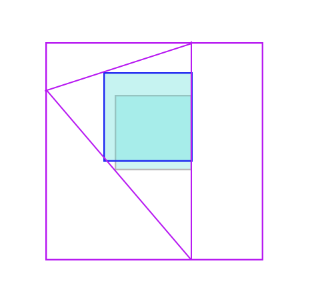
先将小正方形的一边作延长线与大正方形相交，之后再在对边上任取一点相连成三角形。
我们会发现此时的正方形不是此时可以
此时的三角形可以容纳最大的正方形。（大的那个才是）
之后再引入一个结论：不管在对边上取哪个点所能容纳的最大正方形面积不变。（这个也非常好证，相似即可）
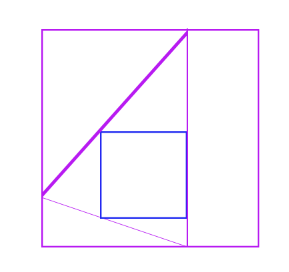那么我们之后将小正方形的四条边都画上这样的三角形。
那这样答案就显而易见了。我们只需要在四个方向上画出这样的三角形，只要有其中任意一个可以将这个三角形包含在内那么就是yes，都没有那么就是no。
那么就可以得到下列的算式：
(x+b-b)/(x+b) = b/a （这是此时往左构造三角形得到的最大正方形的面积）
如果当前的正方形比他小那么就是yes了。得到(x+b-b) / (x+b) >= b / a
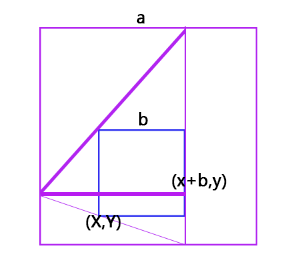
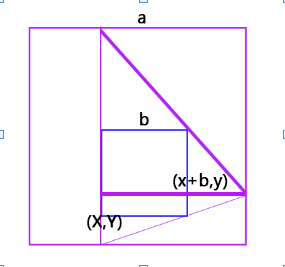其他两幅因为懒就不放上来了。
之后再根据其他几幅图可以得到总的式子：
(x+b-b) / (x+b) >= b / a
(a-x-b) / (a-x) >= b / a
(y+b-b) / (y+b) >= b / a
(a-y-b) / (a-y) >= b / a
只需要满足上面任意一条就是yes了
以下是AC代码：
#include<bits/stdc++.h> using namespace std; #define FastRead ios::sync_with_stdio(0); cin.tie(0); cout.tie(0); #define ll long long int signed main(){ FastRead; auto check = [&](ll h,ll b,ll l){ return h*l <= ((h-l)*b); }; ll t; cin>>t; while(t--){ ll a,b,x,y; cin>>a>>b>>x>>y; if(check(x+b,a,b) || check(a-x,a,b) || check(y+b,a,b) || check(a-y,a,b)){ cout<<"yes "; }else { cout<<"no "; } } }