2019牛客暑期多校训练营(第八场) CDMA

时间限制：C/C++ 1秒，其他语言2秒

空间限制：C/C++ 524288K，其他语言1048576K
Special Judge, 64bit IO Format: %lld

题目描述

  Gromah and LZR have entered the third level. There is a blank grid of size m×mm imes mm×m, and above the grid is a word "CDMA".

  In CDMA Technology, a Technology about computer network, every network node should be appointed a unique binary sequence with a fixed and the same length. Moreover, if we regard 0​ in the sequence as −1, and regard 1​ as +1​, then these sequences should satisfy that for any two different sequences s,t​, the inner product of s,t,t​ should be exactly 0​.

  The inner product of two sequences s,t​ with the same length n equals to ​.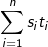

  So, the key to the next level is to construct a grid of size m×m, whose elements are all −1​ or 1​, and for any two different rows, the inner product of them should be exactly 0​.

  In this problem, it is guaranteed that m​ is a positive integer power of 2 and there exists some solutions for input m​. If there are multiple solutions, you may print any of them.

输入描述:

Only one positive integer m​ in one line.   m∈{2k  ∣  k=1,2,⋯ ,10}

输出描述:

Print m​ lines, each contains a sequence with length m​, whose elements should be all −1 or 1​ satisfying that for any two different rows, the inner product of them equals 0​.

You may print multiple blank spaces between two numbers or at the end of each line, and you may print any number of blank characters at the end of whole output file.

输入

2

输出

1 1
1 -1

题意：构造由-1，1组成的m*m矩阵，使得任意两行的对应位置乘积和为0。

题解：

代码：

#include<bits/stdc++.h>
using namespace std;
int ans[1200][1200];
void solve(int x,int y,int n,int w);
int main()
{
  int i,j,n;
  scanf("%d",&n);
  solve(1,1,n,1);
  for(i=1;i<=n;i++)
   for(j=1;j<=n;j++) printf("%d%c",ans[i][j],j==n?'
':' ');
  system("pause");
  return 0;
}
void solve(int x,int y,int n,int w)
{
  if(n==1)
  {
    ans[x][y]=w;
    return ;
  }
  solve(x,y,n/2,w);
  solve(x,y+n/2,n/2,w);
  solve(x+n/2,y,n/2,w);
  solve(x+n/2,y+n/2,n/2,-1*w);
}