前言
又是学新知识的一天呢……
NO.1 精灵魔法
这个题貌似是一个系列的其中一个,有兴趣可以网上搜一下
题目描述
(Tristan) 解决了英灵殿的守卫安排后,便到达了静谧的精灵领地——(Alfheim)。由于(Midgard) 处在 (Alfheim) 和冥界 (Hel) 的中间,精灵族领地尚未受到冥界恶灵的侵入。族长 (Galanodel) 为了帮助米德加尔特抵御外敌,对邪恶亡灵军团使用了高等魔法,从而使得亡灵军团每个士兵的行进速度变得不一致,从而打乱冥王 (Hel)安排的最佳阵型。
由于这个军团离 (Midgard)还很远,因此在抵达 (Midgard) 之前,对于(A),(B) 两个亡灵,若 (A) 的初始位置在 (B) 后面且 (A) 的速度比 (B) 快,(A) 就会冲到 (B) 的前面去。现在 (Galanodel)想知道,会有多少对亡灵之间出现反超现象?
Input
第一行一个整数 (n),表示排成一队的邪恶亡灵军团有多少人。
第二行 (n)个整数,(a_i),表示邪恶亡灵们在数轴上的初始坐标。数据保证这些坐标全部不同。亡灵军团向数轴正方向前进。
第三行 (n)个整数,(v_i),表示邪恶亡灵们的行进速度。
Output
一行一个正整数 (k),表示反超的个数。
Sample Input
3
1 2 3
2 1 3
Sample Output
1
Hint
对于 (30\%)的数据,(1le Nle 1000);
对于(100\%)的数据,(1le Nle 10^5)。
所有数据的绝对值均不超过 (maxlongint)。
分析
因为亡灵位置靠后速度比靠前的亡灵速度大的话就是能够反超,所以根据这个性质我们就可以想出来利用归并排序来进行求解,当然树状数组和线段树也是可以的,这里先分析一下归并排序的方法:
其实这个题相当与归并排序的一个板子题,需要处理的就是进行一下离散化,然后就可以愉快的递归排序了。我们首先开一个结构体存储位置和速度,然后根据位置进行排序,因为位置靠后的速度比前边大的就是反超,所以就可以转化为求逆序对的个数即可,当然,我们排序的过程就已经进行好了离散化了,只需要用一个记录数组来记录下来排序后的所有速度即可。
代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int maxn = 1e5+10;
int n;
struct Node{
ll pos,v;
}a[maxn];
ll ans;
ll jl[maxn];
ll b[maxn];
bool cmp(Node a,Node b){
return a.pos<b.pos;
}
void Merge(int l,int mid,int r){
int i=l,j=mid+1,k=0;//左边从l到mid,右边从mid+1到r
while(i<=mid && j<=r){//左右都不为空
if(jl[i]<=jl[j])b[++k] = jl[i++];//左边的小于右边的,另一个数组记录下小的数
else {//左边大于右边
ans+=mid-i+1;//从左边当前位置到mid和右边的全部能组成逆序对
b[++k] = jl[j++];//另一个数组记录小的数
}
}
while(i<=mid){//没有扫完就继续记录
b[++k] = jl[i++];
}
while(j<=r){//同上
b[++k] = jl[j++];
}
for(i=l,k=1;i<=r;++i,++k){//重新记录排好序的数组
jl[i] = b[k];
}
}
void Merge_sort(int l,int r){//归并排序递归
if(l<r){
int mid = (l+r)>>1;
Merge_sort(l,mid);
Merge_sort(mid+1,r);
Merge(l,mid,r);
}
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;++i){
scanf("%lld",&a[i].pos);
}
for(int i=1;i<=n;++i){
scanf("%lld",&a[i].v);
}
sort(a+1,a+n+1,cmp);//排序进行离散化
for(int i=1;i<=n;++i){//记录每个点的速度
jl[i] = a[i].v;
}
Merge_sort(1,n);
printf("%lld
",ans);
return 0;
}
NO.2 最小环
看到题目会想到(Floyd),看到数据范围还是算了吧,所以用最短路。
题目描述
她走的悄无声息,消失的无影无踪。
至今我还记得那一段时间,我们一起旅游,一起游遍山水。到了最终的景点,她却悄无声息地消失了,只剩我孤身而返。
现在我还记得,那个旅游区可以表示为一张由(n)个节点(m)条边组成无向图。我故地重游,却发现自己只想尽快地结束这次旅游。我从景区的出发点(即 (1) 号节点)出发,却只想找出最短的一条回路重新回到出发点,并且中途不重复经过任意一条边。
即:我想找出从出发点到出发点的小环。
Input
每个测试点有多组测试数据。
第一行有一个正整数(T),((Tle 10)),表示数据组数。
接下来对于每组数据,第一行有两个正整数 (n,m),((nle 10^4,mle 4×10^4)) 分别代表图的点数和边数。
接下来有(m)行,每行三个整数(u,v,d)表示(u,v)之间存在一条长度为 (d,(dle 10^3))的路径。保证不存在重边,自环。
Output
对于每组测试数据,输出题目中所求的最小环的长度。无解输出 (−1) 。
Sample Input
2
3 3
1 2 1
2 3 1
3 1 1
4 5
1 2 2
2 3 2
3 4 2
1 4 2
1 3 5
Sample Output
3
8
分析
题目超级狗血……我从网上找的完整版。直接看题:
首先肯定是求最小环了,但是(Floyd)又不能用,所以考虑利用最短路。
那么怎么求呢,因为如果有环的话,无向图还不能经过重边,所以我们把出去的那个点的回路断开,也就是置为极大值,然后跑从出去的那个点到(1)号节点的最短路,最后统计最小值就行了。
代码
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e5+10;
struct Node{
int v,next,val;
}e[maxn<<1];
int ans = 0x3f3f3f3f;
int head[maxn],dis[maxn],vis[maxn];
int tot=1;
void Add(int x,int y,int z){
e[++tot].v = y;
e[tot].next = head[x];
head[x] = tot;
e[tot].val = z;
}
priority_queue<pair<int,int> >q;
void Dij(int x){//堆优化最短路
memset(dis,0x3f,sizeof(dis));
memset(vis,0,sizeof(vis));
dis[x] = 0;
q.push(make_pair(0,x));
while(!q.empty()){
int y = q.top().second;
q.pop();
if(vis[y])continue;
vis[y] = 1;
for(int i=head[y];i;i=e[i].next){
int v = e[i].v;
if(dis[v] > dis[y]+e[i].val){
dis[v] = dis[y] + e[i].val;
q.push(make_pair(-dis[v],v));
}
}
}
}
void Init(){
memset(e,0,sizeof(e));
memset(head,0,sizeof(head));
tot=1;ans=0x3f3f3f3f;
}
void Solve(){
int n,m,s;
cin>>n>>m;
for(int i=1;i<=m;++i){//双向建图
int x,y,z;
cin>>x>>y>>z;
Add(x,y,z);
Add(y,x,z);
}
for(int i=head[1];i;i=e[i].next){
int v = e[i].v;
int w = e[i].val;
e[i^1].val = 0x3f3f3f3f;//出点到1的反向边权置为极大,相当与断开
Dij(v);//跑最短路
ans = min(ans,dis[1]+w);//最后加上一段的边权
e[i^1].val = w;//恢复
}
if(ans == 0x3f3f3f3f)printf("-1
");//ans没变说明没有符合要求的情况
else printf("%d
",ans);
}
int main(){
int T;
cin>>T;
while(T--){
Init();
Solve();
}
return 0;
}
NO.3 LGTB 与序列
题目描述
(LGTB) 有一个长度为 (N) 的序列 (A),现在他想构造一个新的长度为 (N) 的序列 (B),使得 (B) 中的任意两个数都互质。并且他要使
最小,请输出最小值。
Input
第一行包含一个数 (N)代表序列初始长度。
接下来一行包含 (N)个数 (A_1,A_2,…,A_N),代表序列 (A) 。
Output
输出包含一行,代表最小值。
Sample Input
5
1 6 4 2 8
Sample Output
3
Hint
样例解释:(B={1,5,3,2,7}),1与任何数都互质。
对于 (40\%)的数据, (1le Nle 10)。
对于 (100\%)的数据, (1le Nle 100,1le A_ile 30)。
分析
看到这范围,可能很少会有人想到状压(dp),但是深入思考一下,因为(A_ile 30),而(B_i)最小为(1),所以我们可以得到(B_i)最大为(58),因为一旦超过(58),差的绝对值肯定还不如(1),因为(1)是质数,所以最大到(58),然后我们找到其中的质数打表打出来,一共是(16)个,那么我们就可以用这个作为状态,即含有哪个质因子。
所以我们定义(f[i][j])为前(i)个数,使用质因子状态为(j)的答案,然后开始愉快的状态转移。
我们首先初始化出来(1)到(58)含有质因子的状态,存在一个数组里然后枚举质因子和状态,进行状态转移,假设(j)为当前状态,(k)为枚举(B_i)的所有情况,那么状态转移方程就是:
最后枚举每个状态,取最小值。
不要忘了,如果(N)大于16的话,后边都取(1),还要继续统计。因为要使绝对值最小,所以降序排序,最终的答案就是最小的。
代码
#include<bits/stdc++.h>
using namespace std;
const int maxn = 110;
int a[maxn];
int f[17][1<<17];
int n,prime[17];
int ste[maxn];
void Init(){//打表初始化
prime[0] = 0;
prime[1] = 2;
prime[2] = 3;
prime[3] = 5;
prime[4] = 7;
prime[5] = 11;
prime[6] = 13;
prime[7] = 17;
prime[8] = 19;
prime[9] = 23;
prime[10] = 29;
prime[11] = 31;
prime[12] = 37;
prime[13] = 41;
prime[14] = 43;
prime[15] = 47;
prime[16] = 53;
}
bool cmp(int a,int b){//降序排序
return a>b;
}
int main(){
cin>>n;
for(int i=1;i<=n;++i){
cin>>a[i];
}
sort(a+1,a+n+1,cmp);
Init();
for(int i=1;i<=58;++i){
for(int j=1;j<=16;++j){
if(i<prime[j])break;
else if(i%prime[j] == 0){
ste[i] |= (1<<(j-1));//从1到58每个数的状态预处理
}
}
}
memset(f,0x3f,sizeof(f));
f[0][0] = 0;//f数组初始化
int ms = (1<<16)-1;//总状态
for(int i=1;i<=min(n,16);++i){//枚举质因子
for(int j=0;j<=ms;++j){//枚举状态
for(int k=1;k<=58;++k){//枚举所有Bi的可能
if(!(ste[k]&j)){//上一状态还没有k的质因子
int s = j|ste[k];//使用k的质因子
f[i][s] = min(f[i][s],f[i-1][j]+abs(a[i]-k));//转移
}
}
}
}
int ans = 0x3f3f3f3f;
for(int i=0;i<=ms;++i){//枚举所有状态,统计答案
ans = min(ans,f[min(16,n)][i]);
}
if(n>16){//大于16继续统计
for(int i=17;i<=n;++i){
ans += abs(a[i]-1);
}
}
cout<<ans<<endl;
}
NO.4 步步为零
真就步步为零……
题目描述
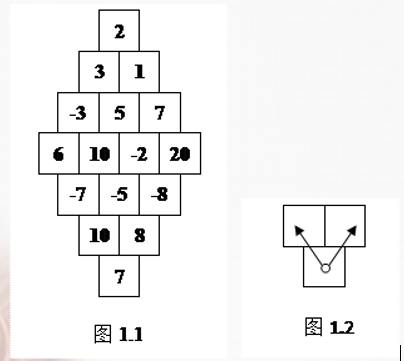
你是否听说过这个游戏?游戏者在一张特殊的表格中按照规则跳动,使得跳到的数字经过加号和减号的连接,尽可能的逼近零。表格通常是如图 (1.1) 所示的形状,大小由中间一行的方格数 (N) 决定(图 (1.1) 就是一个 (N=4)的例子)。
游戏者通常是从最下面的方格出发,按照如图 (1.2)所示的规则在表格中跳动,当游戏者跳到最顶端的方格时,游戏结束。在游戏未结束前,游戏者不允许跳到表格外。
将游戏者跳到的 (2 imes N−1)个数字依次写下来,在每两个相邻的数字中间加上加号或减号,使得计算结果最接近零。
例如对于图 (1.1)
所示的表格,最好的跳动及计算方案是:(7+8+(−5)+(−2)−5−1−2=0) 或 (7+10+(−7)−6+(−3)−3+2=0) 或 (7+10+(−5)−10−5+1+2=0) 或 (7+10+(−5)+(−2)−5−3−2=0) 。
Input
输入文件的第一行是 (N(Nle 50))
接下来 (2 imes N−1) 行给出了表格中每行的每个方格中的数字
第 (i+1) 行的第 (j) 个数字对应于表格中第 (i) 行的第 (j)个数字。
文件中第二行的数字表示的是表格顶端的方格中的数字。文件中所有的数字都是整数,同一行相邻的两个数字间用空格符隔开。
Output
输出文件只有一行,是你所求出的最接近零的计算结果的绝对值。
Sample Input
4
2
3 1
-3 5 7
6 10 -2 20
-7 -5 -8
10 8
7
Sample Output
0
Hint
表格中的所有数字大于等于(−50),小于等于(50)。
分析
这个题其实就是dp,还是个线性的,但是转移非常的费劲和难想。首先看一个简单的图:
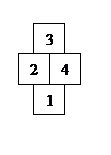
要想求从(1)到(3)的最小绝对值,那么肯定是从(1)到(2)和(1)到(4)最后加上或者减去3来得到,我们根据这个进行转移。
需要注意的是,我们需要开一个数组来判断某一阶段能否到达一个值。
因为有卡内存,所以开滚动数组。
代码
#include<bits/stdc++.h>
using namespace std;
const int maxn = 36;
int a[maxn<<1][maxn],n,tot;
bool f[maxn<<1][maxn][6005];//f[i][j][k]表示从最后一行到i行j列能否组成k
bool judge(int x){//判断是否超过最大或最小值
if(x<0 || x>2*tot)return 0;
return 1;
}
int main(){
cin>>n;
for(int i=1;i<=n;++i){
int Max = 0;//求出每行最大值
for(int j=1;j<=i;++j){
cin>>a[i][j];
a[i][j] = abs(a[i][j]);//变为正数好处理
Max = max(Max,a[i][j]);
}
tot += Max;//记录总和
}
for(int i=1;i<n;++i){
int Max = 0;//同上
for(int j=1;j<=n-i;++j){
cin>>a[n+i][j];
a[n+i][j] = abs(a[n+i][j]);
Max = max(Max,a[n+i][j]);
}
tot+=Max;
}
f[2*n-1][1][tot] = 1;//第一个状态为真,为好处理,全部加上tot,那么tot为0,此时0到tot×2为-tot~tot
int now = 0;
for(int i=2*n-1;i>n;--i){//下边的n-1行
for(int j=1;j<=2*n-i;++j){//列
for(int k=0;k<=2*tot;++k){
if(f[i][j][k]){//状态合法
now = k+a[i][j];
if(judge(now)){//当前没超过最大低于最小
f[i-1][j][now] = f[i-1][j+1][now] = 1;
}
now = k-a[i][j];
if(judge(now)){//同上
f[i-1][j][now] = f[i-1][j+1][now] = 1;
}
}
}
}
}
for(int i=n;i>=1;i--){//上边的n行
for(int j=1;j<=i;++j){
for(int k=0;k<=2*tot;++k){
if(f[i][j][k]){
now=k+a[i][j];
if(judge(now))
f[i-1][j][now]=f[i-1][j-1][now]=1;
now=k-a[i][j];
if(judge(now))
f[i-1][j][now]=f[i-1][j-1][now]=1;
}
}
}
}
int ans = 0x3f3f3f3f;
for(int i=0;i<=2*tot;++i){
if(f[0][0][i] || f[0][1][i]){//符合要求就取最小值。
ans = min(ans,abs(i-tot));
}
}
cout<<ans<<endl;
}