打鼹鼠

在这个“打鼹鼠”的游戏中，鼹鼠会不时地从洞中钻出来，不过不会从洞口钻进去（鼹鼠真胆大……）。洞口都在一个大小为n(n≤1024)的正方形中。这个正方形在一个平面直角坐标系中，左下角为(0,0)，右上角为(n-1,n-1)。洞口所在的位置都是正点，即横坐标、纵坐标都为整数的点。而SuperBrother也不时地会想知道某一个范围的鼹鼠总数。这就是你的任务。

---

二维树状数组的模板，然而并不会写，于是现场脑补

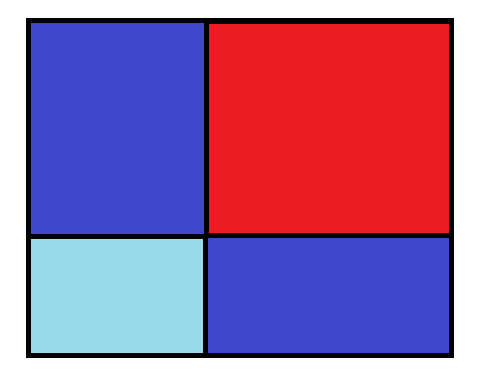
 红色的地方是我们要求的，蓝色的部分是重复的，要减去，然后浅蓝色的部分是重复减去的，要再加回来

下面给出代码：

#include<iostream>
#include<algorithm>
#include<cstring>
#include<string>
#include<cmath>
#include<cstdio>
#include<cstdlib>
using namespace std;
inline int rd(){
    int x=0,f=1;
    char ch=getchar();
    for(;!isdigit(ch);ch=getchar()) if(ch=='-') f=-1;
    for(;isdigit(ch);ch=getchar())
        x=x*10+ch-'0';
    return x*f;
}
inline void write(int x){
    if(x<0) putchar('-'),x=-x;
    if(x>9) write(x/10);
    putchar(x%10+'0');
    return ;
}
int c[1026][1026];
int n,m;
inline int lowbit(int x){return x&(-x);}
inline void change(int i,int j,int k){
    for(;i<=n;i+=lowbit(i))
        for(int y=j;y<=n;y+=lowbit(y))
            c[i][y]+=k;
}
inline int solve(int i,int j){
    int ans=0;
    for(;i>0;i-=lowbit(i)){
        for(int y=j;y>0;y-=lowbit(y)){
            ans+=c[i][y];
        }
    }
    return ans;
}
int main(){
    n=rd();
    while(scanf("%d",&m)){
        if(m==1){
            int x=rd(),y=rd();
            x++,y++;
            int k=rd();
            change(x,y,k);
        }
        if(m==2){
            int a1=rd(),b1=rd(),a2=rd(),b2=rd();
            a1++,b1++,a2++,b2++;
            write(solve(a2,b2)-solve(a2,b1-1)-solve(a1-1,b2)+solve(a1-1,b1-1));puts("");
        }
        if(m==3) break;
    }
    return 0;
}