Tarjan 算法一种由Robert Tarjan提出的求解有向图强连通分量的算法,它能做到线性时间的复杂度。(每个点只经过一次)
说到Tarjan,我们首先要说到的肯定是有向图,因为无向图没有这么一个东西
这句要从Tarjan算法的定义讲起了
我们定义:
如果两个顶点可以相互通达,则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通,称G是一个强连通图。有向图的极大强连通子图,称为强连通分量(strongly connected components)。
这句话在网上是非常普及的,然而说白了就是一个联通块,从每两个点之间都能互相到达,就是一个强连通分量
而Tarjan的作用,就是很快的求出一个有向图中强连通分量的个数,以及每个强连通分量中的点
具体是如何实现的
我们记录两个数组
DFN和LOW,他们分别记录每个点的DFS序,和每个点能回到的点的最小的DFS序
这么说可能不太清晰
我们来举个栗子:(方便起见,我们把走到的点表为红色)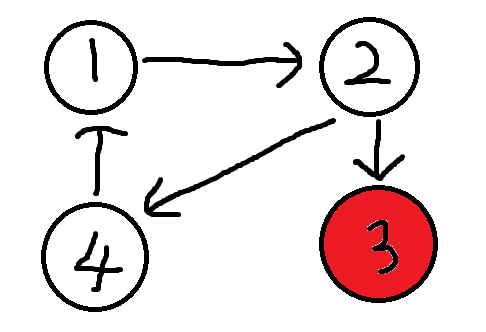
按照惯例,我们从点1出发,首先是到了他的儿子2,然后是3
此时 DFN[1]=1
LOW[1]=1
DFN[2]=2;
LOW[2]=2;
DFN[3]=3;
LOW[3]=3;
DFN[4]=0;
LOW[4]=0;
我们发现三没有儿子了,也就是说LOW[3]的值无法改变了,又发现DFN[3]=LOW[3]
所以我们就知道了3构成了一个强连通分量
然后继续走
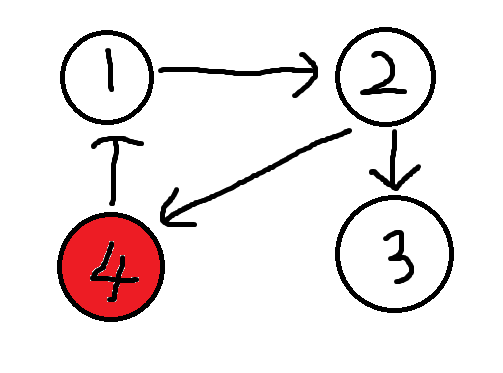
我们到了2的另一个儿子处
此时 DFN[1]=1
LOW[1]=1
DFN[2]=2;
LOW[2]=2;
DFN[3]=3;
LOW[3]=3;
DFN[4]=4;
LOW[4]=4;
然后就到了最重要的一步
4有一个儿子是1,但是1已经走过了
所以我们可以直接更新LOW[4]的值
此时 DFN[1]=1
LOW[1]=1
DFN[2]=2;
LOW[2]=2;
DFN[3]=3;
LOW[3]=3;
DFN[4]=4;
LOW[4]=1;
既然1已经走过了我们就不用再走了(要不然怎么线性)
开始回溯
我们更新LOW[2]的值
此时 DFN[1]=1
LOW[1]=1
DFN[2]=2;
LOW[2]=1;
DFN[3]=3;
LOW[3]=3;
DFN[4]=4;
LOW[4]=1;
然后回到1,Tarjan算法结束
以上是Tarjan的具体运算过程
但是其中还有一些简单的染色操作
就不细讲了(代码中给了注释)
下面给出代码:(写代码过程中电脑突然卡了,结果刚写完的模板和注释都没了 伤心到变形QAQ)
#include<iostream> #include<cmath> #include<cstdio> #include<cstdlib> #include<cstring> #include<string> #include<algorithm> #include<stack> using namespace std; inline int min(int a,int b){return a<b?a:b;} inline int max(int a,int b){return a>b?a:b;} inline int rd(){ int x=0,f=1; char c=getchar(); for(;!isdigit(c);c=getchar()) if(c=='-') f=-1; for(;isdigit(c);c=getchar()) x=x*10+c-'0'; return x*f; } inline void write(int x){ if(x<0) putchar('-'),x=-x; if(x>9) write(x/10); putchar(x%10+'0'); } int n,m; int head[100006]; int nxt[100006],to[100006]; int total=0; int dfn[100006],low[100006]; int tot=0; int book[100006],color[100006]; int cnt=0; stack <int> s; void add(int x,int y){ total++; to[total]=y; nxt[total]=head[x]; head[x]=total; return ; } void tarjan(int x){ dfn[x]=++tot; low[x]=dfn[x]; book[x]=1; s.push(x); for(int e=head[x];e;e=nxt[e]){ if(!dfn[to[e]]){//如果没有走过,就扩展这个点 tarjan(to[e]); low[x]=min(low[x],low[to[e]]); } else if(book[to[e]]) low[x]=min(low[x],dfn[to[e]]);//在栈中就代表这个点走过,而他可以回溯到的点,他的父亲也可以 } if(dfn[x]==low[x]){//如果一个点的dfn与low相等,代表以它为根的子图是强联通分量 color[x]=++cnt;//染色 book[x]=0; while(!s.empty()&&s.top()!=x){//把与x联通的点都出栈 color[s.top()]=cnt; book[s.top()]=0; s.pop(); } s.pop(); } return ; } int main(){ n=rd(),m=rd(); for(int i=1;i<=m;i++){ int x=rd(),y=rd(); add(x,y);//有向图单向连边 } for(int i=1;i<=n;i++) if(!dfn[i]) tarjan(i);//避免有的点不连通 printf("%d ",cnt); for(int i=1;i<=cnt;i++){ for(int j=1;j<=n;j++) if(color[j]==i) printf("%d ",j);//其实是可以写在tarjan过程中的的,但是会变成dfs序的倒序 puts(""); } return 0; }