11.10的一套题

注：所有题目的时间限制均为 1s，内存限制均为 256MB。
1．第K小数 (number.cpp/c/pas)

【问题描述】

有两个正整数数列，元素个数分别为N和M。从两个数列中分别任取一个数 相乘，这样一共可以得到N*M个数，询问这N*M个数中第K小数是多少。

【输入格式】

输入文件名为number.in。

输入文件包含三行。

第一行为三个正整数N,M和K。

第二行为N个正整数，表示第一个数列。

第三行为M个正整数，表述第二个数列。

【输出格式】

输出文件名为number.out。

输出文件包含一行，一个正整数表示第K小数。

【输入输出样例1】

number.in

2 3 4

1 2

2 1 3

number.out  

3

【输入输出样例2】

number.in

5 5 18

7 2 3 5 8

3 1 3 2 5

number.out  

16

【数据规模与约定】

/*
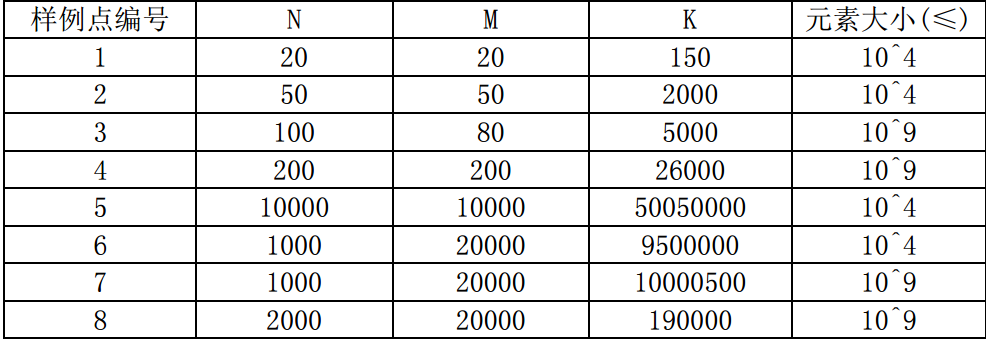
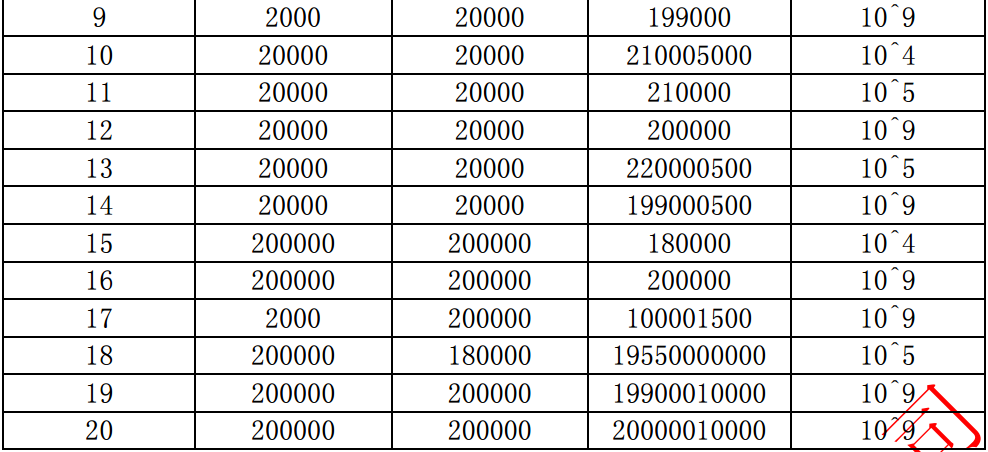
二分答案 
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define LL long long
#define maxn 200010
using namespace std;
LL n,m,w,ans,l,r;
LL a[maxn],b[maxn];
LL init()
{
    LL x=0,f=1;char c=getchar();
    while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
    while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
    return x*f;
}
int judge(LL x)
{
    LL sum=0,p=m;
    for(int i=1;i<=n;i++)
    {
        while(p>=1&&a[i]*b[p]>x)p--;
        sum+=p;
    }
    return sum>=w;
}
int main()
{
    freopen("number.in","r",stdin);
    freopen("number.out","w",stdout);
    n=init();m=init();w=init();
    for(int i=1;i<=n;i++)a[i]=init();
    for(int i=1;i<=m;i++)b[i]=init();
    sort(a+1,a+n+1);sort(b+1,b+m+1);
    l=0;r=a[n]*b[m];
    while(l<=r)
    {
        LL mid=(l+r)/2;
        if(judge(mid))
        {
            ans=mid;
            r=mid-1;
        }
        else
          l=mid+1;
    }
    cout<<ans<<endl;
    return 0;
}

2． dwarf tower (dwarf.cpp/c/pas)

【问题描述】

Vasya在玩一个叫做"Dwarf Tower"的游戏，这个游戏中有n个不同的物品， 它们的编号为1到n。现在Vasya想得到编号为1的物品。 获得一个物品有两种方式：

1. 直接购买该物品，第i件物品花费的钱为ci

2. 用两件其他物品合成所需的物品，一共有m种合成方式。

请帮助Vasya用最少的钱获得编号为1的物品。

【输入格式】

第一行有两个整数n,m(1<=n<=10000,0<=m<=100000)，分别表示有n种物品以 及m种合成方式。

接下来一行有n个整数，第i个整数ci表示第i个物品的购买价格，其中 0<=ci<=10^9。

接下来m行，每行3个整数ai,xi,yi，表示用物品xi和yi可以合成物品ai，其 中(1<=ai,xi,yi<=n; ai<>xi, xi<>yi, yi<>ai)

【输出格式】
一行，一个整数表示获取物品 1 的最少花费。
输入样例：
5 3           
5 0 1 2 5
5 2 3
4 2 3
1 4 5

 输出样例：

2

【数据规模与约定】

60%的数据， n<=100
100%的数据， n<=10000， m<=100000

#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#define maxx 10010
#define maxn 100010
using namespace std;
int n,m,topt;
int first[maxx],f[maxx],dis[maxx];
struct edge
{
    int to;
    int v;
    int next;
}e[maxn*2];
queue<int>q;
int init()
{
    int x=0,f=1;char c=getchar();
    while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
    while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
    return x*f;
}
void add(int x,int y,int z)
{
    topt++;
    e[topt].to=y;
    e[topt].v=z;
    e[topt].next=first[x];
    first[x]=topt;
}
void spfa()
{
    for(int i=1;i<=n;i++)
    {
        q.push(i);
        f[i]=1;
    }
    while(!q.empty())
    {
        int now=q.front();
        q.pop();f[now]=0;
        for(int i=first[now];i;i=e[i].next)
        {
            int to=e[i].to,v=e[i].v;
            if(dis[to]>dis[now]+dis[v])
            {
                dis[to]=dis[now]+dis[v];
                if(!f[to])
                {
                    f[to]=1;
                    q.push(to);
                }
            }
        }
    }
}
int main()
{
    freopen("dwarf.in","r",stdin);
    freopen("dwarf.out","w",stdout);
    n=init();m=init();
    for(int i=1;i<=n;i++)dis[i]=init();
    for(int i=1;i<=m;i++)
    {
        int x,y,z;
        z=init();x=init();y=init();
        add(x,z,y);add(y,z,x);
    }
    spfa();
    printf("%d
",dis[1]);
    return 0;
}

3． abcd (abcd.cpp/c/pas)

【问题描述】

有4个长度为N的数组a,b,c,d。现在需要你选择N个数构成数组e，数组e满足 a[i]≤e[i]≤b[i]以及

并且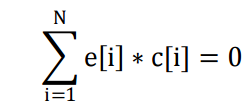使得最大。

【输入格式】

输入文件名为abcd.in。

输入文件共 N+1 行。

第 1 行包含1个正整数N。

第 i+1 行包含4个整数a[i],b[i],c[i],d[i]。

【输出格式】

输出文件名为abcd.out。

输出共1行，包含1个整数，表示所给出公式的最大值。

输入数据保证一定有 解。

【输入输出样例1】

abcd.in

5

- 1 1 2 5

-2 2 1 2

0 1 1 3

-2 -1 3 10

-2 2 3 9

 

abcd.out  

2

【输入输出样例2】

abcd.in

10

1 10 1 7

-10 10 2 0

-10 10 2 2

-10 10 2 0

1 10 1 0

-10 10 2 0

10 10 2 0

1 10 1 0

-10 10 2 0

1 10 1 0

abcd.out  

90

【输入输出样例3】

abcd.in

10

1 10 1 0

-10 10 2 2

-10 10 2 2

-10 10 2 2

1 10 1 0

-10 10 2 2

-10 10 2 2

1 10 1 0

-10 10 2 2

1 10 1 0 

 

abcd.out

-4

【数据规模与约定】

对于 20%的数据， N≤10， -2≤a[i]<b[i]≤2；

对于 60%的数据， N≤50, -20≤a[i]<b[i]≤20；

对于 100%的数据， N≤200， -25≤a[i]<b[i]≤25， 1≤c[i]≤20， 0≤d[i] ≤10000

#include<iostream>
#include<cstdio>
#include<cstring>
#define maxn 210
#define maxx 100010
using namespace std;
int n,m,add,tot,T;
int a[maxn],b[maxn],c[maxn],d[maxn];
int dp[maxx];
int w[maxx],v[maxx];
int init()
{
    int x=0,f=1;char c=getchar();
    while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
    while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
    return x*f;
}
int main()
{
    freopen("abcd.in","r",stdin);
    freopen("abcd.out","w",stdout);
    n=init();
    for(int i=1;i<=n;i++)
    {
        a[i]=init(),b[i]=init(),c[i]=init(),d[i]=init();
        T-=c[i]*a[i];b[i]-=a[i];add+=d[i]*a[i];
    }
    for(int i=1;i<=n;i++)
    {
        int z=1;
        while(z<b[i])
        {
            tot++;
            w[tot]=z*c[i];
            v[tot]=z*d[i];
            b[i]-=z;z=z*2;
        }
        tot++;
        w[tot]=b[i]*c[i];
        v[tot]=b[i]*d[i];
    }
    memset(dp,-127/3,sizeof(dp));
    dp[0]=0;
    for(int i=1;i<=tot;i++)
    {
        for(int j=T;j>=w[i];j--)
        dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
    }
    printf("%d
",dp[T]+add);
    return 0;
}