[机器学习]回归--(Simple LR and Multiple LR)

线性回归是最贴近生活的数据模型之一

简单的线性回归

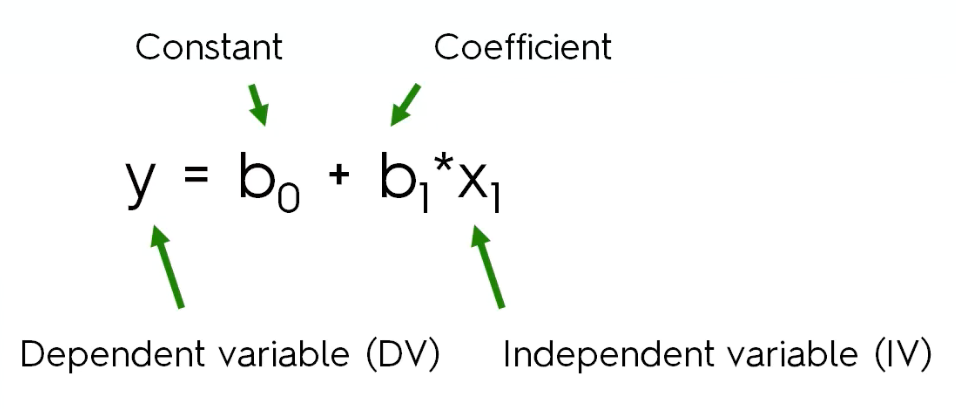
简单的线性回归公式如下：

从公式中我们可以看出，简单线性回归只有一个自变量x1，b1是自变量的系数，y是因变量。x1可能是连续型或者离散型的数据，所以我们需要通过x1找出最合适的系数b1从而得到关于因变量y的曲线。

我们下面用一个例子来说明，这是一个关于工作经验与薪水之间关系的表格。分布如下图所示

我们很容易看出这是符合一个线性回归的模型，下面我们就要做出回归的函数并且对未来数据进行预测。

# Importing the libraries
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

# Importing the dataset
dataset = pd.read_csv('Salary_Data.csv')
X = dataset.iloc[:, :-1].values #除了最后一列的其他列
y = dataset.iloc[:, 1].values   #第二列

# Splitting the dataset into the Training set and Test set
from sklearn.cross_validation import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 1/3, random_state = 0)

下面我们需要做的是通过训练集的X_train与y_train 计算出符合训练集的曲线，然后将测试集的X_test 带入得到的曲线中，得到预测的结果y_pred，最后将预测结果y_pred与测试集中的y_test进行比较，看看是否符合分布，从而确定预测是否准确。

# Fitting Simple LinearRegression to the training set
from sklearn.linear_model import LinearRegression
regressor = LinearRegression()
regressor.fit(X_train,y_train) # 通过train集找到曲线

# 对测试集进行预测
y_pred = regressor.predict(X_test)

# visualising the Traning set results
plt.scatter(X_train, y_train, color = 'red')
plt.plot(X_train, regressor.predict(X_train), color = 'blue')
plt.title('Salary vs Experience(Traning set)')
plt.xlabel('Year of Experience')
plt.ylabel('Salary')
plt.show()

通过学习我们可以得到训练曲线

下面我们导入测试数据

plt.scatter(X_test, y_test, color = 'red')
plt.plot(X_train, regressor.predict(X_train), color = 'blue')
plt.title('Salary vs Experience(Traning set)')
plt.xlabel('Year of Experience')
plt.ylabel('Salary')
plt.show()

这里需要注意两点

第一，在导入测试集时我们依然使用训练集得到的曲线，所以我们的plot函数中参数不便，当然如果你用测试集的数据应该也会得到相同的曲线。

第二有的人觉得既然需要预测数据应该将y_test 替换成 y_pred。 其实不需要这样的。因为我们y_pred 上的点应该都是和曲线高度重合的

多重线性回归（Multiple Linear Regression）

多重线性回归将会不只有一个自变量，并且每个自变量拥有自己的系数且符合线性回归。

在建立多重线性回归之前，有这么几个前提必须要注意一下，这些有助于你判断数据是否适合使用多重线性回归：
1， 线性（linearity）
2， 同方差（Homoscedasticity）

3， 多元正态性（Multivariate normality）  

      多因素共同影响分布结果

4， 错误的独立性（independence of errors）

      每一个变量产生的错误将会独立的影响预测结果，不会对其他变量产生影响

5， 多重共线性的缺乏（lack of multicollinearity）

      变量之间存在高度相关关系而使得回归估算不准确，如接下来要提到的虚拟变量陷阱（dummy variable trap）有可能触发多重共线性的问题

虚拟变量陷阱（Dummy variable trap）

在回归预测中我们需要所有的数据都是numeric的，但是会有一些非numeric的数据，比如国家，省，部门，性别。这时候我们需要设置虚拟变量（Dummy variable）。做法是将此变量中的每一个值，衍生成为新的变量，是设为1，否设为0.举个例子，“性别"这个变量,我们可以虚拟出“男”和"女"两虚拟变量，男性的话“男”值为1，"女"值为,；女性的话“男”值为0，"女"值为1。

但是要注意，这时候虚拟变量陷阱就出现了。就拿性别来说，其实一个虚拟变量就够了，比如 1 的时候是“男”， 0 的时候是"非男"，即为女。如果设置两个虚拟变量“男”和“女”，语义上来说没有问题，可以理解，但是在回归预测中会多出一个变量，多出的这个变量将会对回归预测结果产生影响。一般来说，如果虚拟变量要比实际变量的种类少一个。

所以在多重线性回归中，变量不是越多越好，而是选择适合的变量。这样才会对结果准确预测。

建立模型

我们可以通过以下五个步骤建立回归模型：（stepwise Regression）

1， 确立所有的可能（变量all in）
建立所有的个模型包含所有可能的变量

2, 逆向消除（backward elimination）
(1)选择一个差异等级（significance level）比如SL=0.05， 0.05 意味着此变量对结果有95%的贡献。 P(A|B) = 0.05
(2)将所有的变量放进你的模型中。
(3)选择P值最高的变量，如果P>SL。到第四步，否则结束，完成建模。关于变量P值，统计软件可以计算出并选择最高P值的变量
(4)移除此变量，并重新进行第三步。

有关逆向消除和逐步回归的方法，可以参考一下两个链接：

Backward elimination and stepwise regression
Variable Selection

3, 正向选择（forward selection）
(1)选择一个差异等级（significance level）比如SL=0.05
(2)建立所有的简单回归的模型，并找到最小的P值
(3)确立一个简单模型，并将拥有最小P值的变量加入此模型
(4)如果P>SL,模型建立成功，否则在进行第三步

4，双向消除（bidirectionnal elimination）
同时进行逆向消除和正向选择。

*所有可能的模型：意思是所有变量排列组合成的模型，如果有N个变量，那么一共会有2的N次方个模型（2^N-1）
在R语言中，每一个变量后面会用星号表示此变量对回归模型的影响，星号越多越重要。

Stepwise Regression 这是宾夕法尼亚州立大学的讲解。我觉得挺不错的
另外，其实这几步不是很难，关键的一点是SL值的确定。还有就是P值的生成。

如何计算P值（p-value）

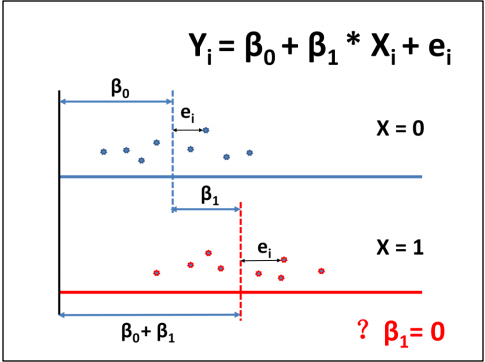
假定有两组人群，一组x=0，另一组x=1。从两组中各随机抽取2个个体，测量Y
的值，如图所示，看看这两组的Y是否相同？
现在各组再多抽取若干个体，数据如图所示，可以计算各组的均数，这两个均
数不在同一条线上，这是从所抽取的样本中估计出来的。从样本中得到的两个
均数不等于两组总体的均数，从样本中得到的两均数距离不等于两个总体均数
的差，t 检验是根据两样本均数及两样本的标准差，计算如果两总体均数相同的
话，抽样得到两样本均数差达如此之大或更大的可能性多大，就是p 值，p值
<0.05，表示两者之间的距离显著。
现在看回归分析，建立回归方程如上所示。从方程中看，当x=0时，Y=β0；当x=1
时，Y=β0 + β1。因此，β0表示X=0组Y的均数，β1表示X=1组Y的均数与X=0组Y的均
数的差，ei是每个个体与其所在组均数的差。因此回归方程对β1= 0 的检验等同
于t检验两组均数的比较。

用Python进行操作

我们可以使用之前建立的模板，将数据导入。

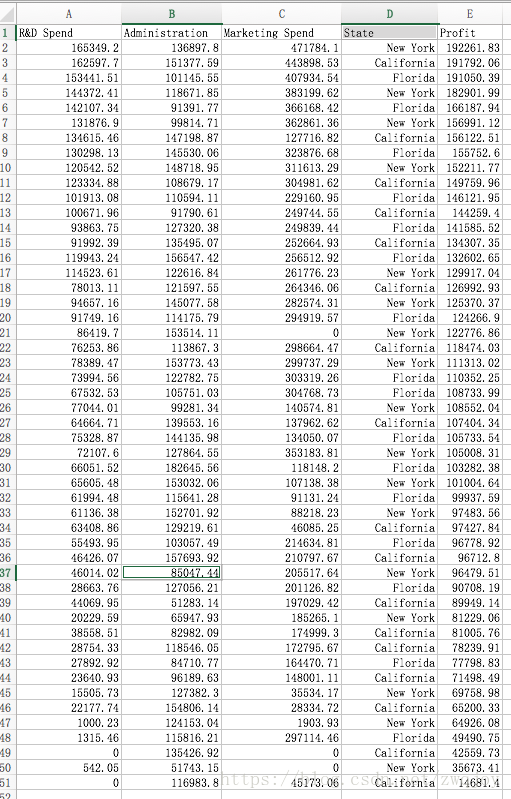
今天我们使用一个多变量对商业profit影响的数据集。

在此数据集中，我们确定前四个变量 X（R&D Speed, Administration, Marketing Speed, State）为自变量。

最后一个profit为因变量 y。

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

# Importing the dataset
dataset = pd.read_csv('50_Startups.csv')
X = dataset.iloc[:, :-1].values
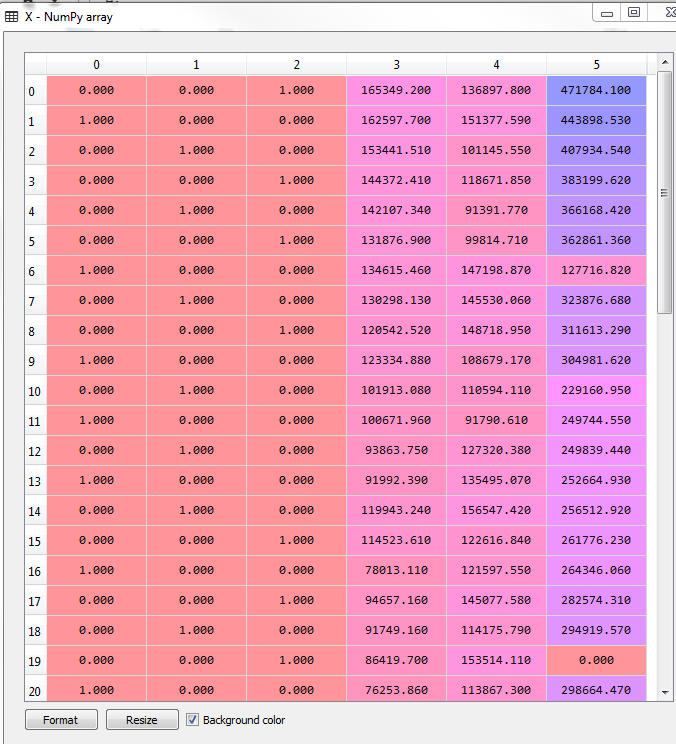
y = dataset.iloc[:, 4].values

由于数据中包含state变量，我们用虚拟变量代替

from sklearn.preprocessing import LabelEncoder, OneHotEncoder
labelencoder = LabelEncoder()
X[:, 3] = labelencoder.fit_transform(X[:, 3])
onehotencoder = OneHotEncoder(categorical_features = [3])
X = onehotencoder.fit_transform(X).toarray()

#为了避免虚拟变量陷阱
X = X[:, 1:] #从1 开始，并非0

将数据集分为训练集和测试集，我们选择test size为0.2（4：1）

from sklearn.cross_validation import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 0)

多重线性回归：

from sklearn.linear_model import LinearRegression
regressor = LinearRegression()
regressor.fit(X_train, y_train)

得到预测结果：

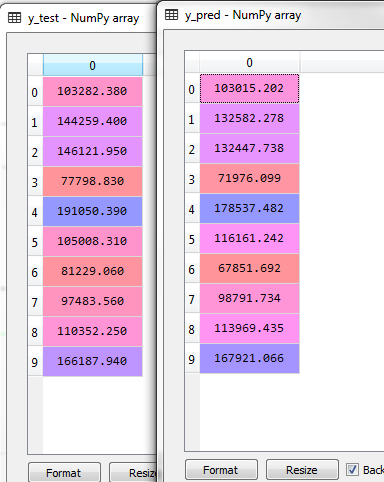
y_pred = regressor.predict(X_test)

我们比较一下预测结果（y_pred）和实际结果(y_test)中的差异

其实很多结果还是很接近的。

这样我们就完成了多元线性回归的建模过程。其实我们与简单线性回归比较一下，代码完全相同.

所以在sklearn的线性回归库中没有简单或者多元的区分。但是多元线性回归很难用图像表示，因为包含多个自变量。