在读研期间,一直在帮导师做技术开发,甚至偶尔做一做美工(帮导师和实验室博士生画个图啥的),算法还是较少接触的,其实,我发现,算法还是蛮好玩的,昨晚看了B站一个美女算法工程师讲了线性回归和逻辑回归两种算法,做下总结吧,不然看了之后过两天就抛在脑后,忘光光了。。视频点击这里。
概念1:回归与分类问题。
1)回归:回归问题模型倾向于一个输入点X对应着一个输出点Y。咱们可以抽象的想象成小学时候学的(Y=aX+b)方程,即X与Y一一对应。
2)分类:分类问题也是类似于回归的一种计算模型,但是,差异就在分类问题的Y值(也称label),更加离散化一些。而且,同一个Y值可能对应着一大批的X值,当然,对应的这些X肯定是有个范围的,所以,分类问题可理解成一定区域的X值(多X)对应着一个Y(单Y)。
概念2:线性回归详解与实例。
1)线性回归:用一个直线较为精准的描述数据之间的关系,每当出现新的数据时(X),可以预测出一个对应的输出值(Y)。
2)实例:房屋面积与房价的对应关系。
训练数据如下:

根据上面的这个训练集,拟合一条直线,表示面积与房价的关系,但是呢,不同的人拟合的直线是不同的,所以,我们必须找到一条最合理的直线。
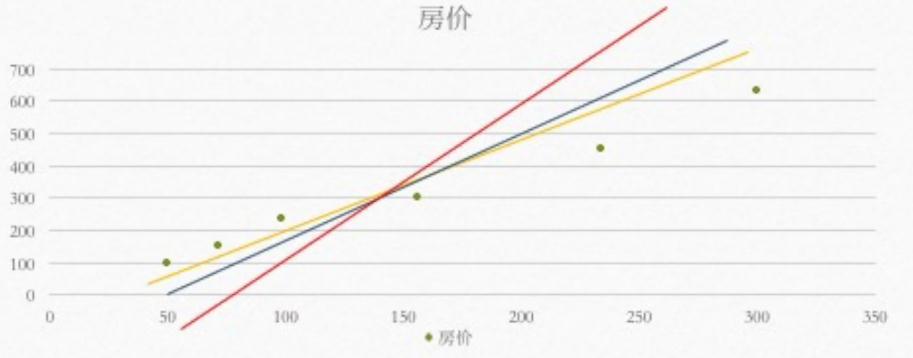
如何找出这条直线,就是要求出各个点到直线的距离,让这个距离最小,那这条直线就是我们要求的。
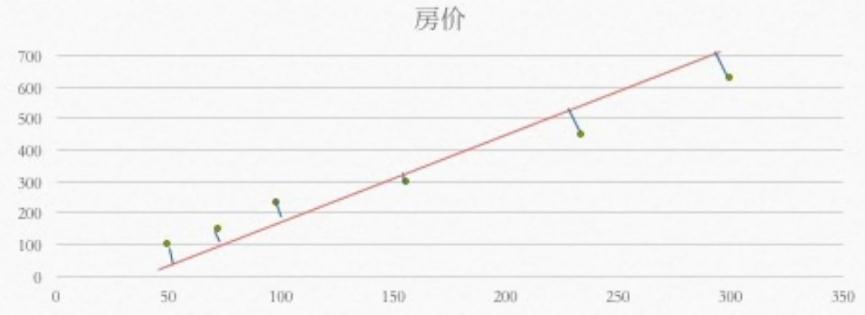
3)总结(3部)
1.构造预测函数(也就是构造那个拟合的直线,这里是多维线性回归)
2.构造损失函数
3.最小化损失函数

概念3:逻辑回归详解。
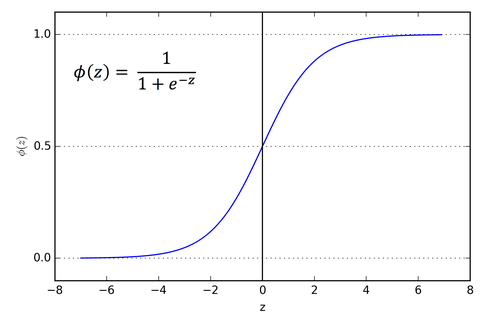
细说:逻辑回归是在线性回归的基础上嵌套了一个sigmoid函数,目的是将线性回归函数的结果映射到sigmoid函数中(如下图)。
我们知道,线性回归的模型是求出输出特征向量Y和输入样本矩阵X之间的线性关系系数θ,满足Y=Xθ。此时我们的Y是连续的,所以是回归模型。
如果我们想要Y是离散的话,怎么办呢?一个可以想到的办法是,我们对于这个Y再做一次函数转换,变为g(Y) -- 即为如下的sigmoid函数。
如果我们令g(Y)的值在某个实数区间的时候是类别A,在另一个实数区间的时候是类别B,以此类推,就得到了一个分类模型。
如果结果的类别只有两种,那么就是一个二元分类模型了。逻辑回归的出发点就是从这来的。
步骤:(构造过程可借鉴这里)
1)构造预测函数
2)构造损失函数
3)最小化损失函数

概念4:两种算法的步骤总结
1)找一个合适的预测函数(hypothesis,h函数),该函数就是我们需要找的分类函数,他用来预测输入数据的判断结果,需要对数据分布有一定的了解,比如是线性函数还是非线性函数。
2)构造一个Cost函数(损失函数),该函数表示预测的输出(h函数)与训练数据类别(Y)之间的偏差,即为(h-Y),综合考虑所有的训练数据的“损失”,记为J(θ)函数,表示所有训练数据与实际数据之间的偏差。
3)J(θ)函数的值越小表示预测函数越准确,所以这一步是找出最小的J(θ)。