数学图形(2.6)Satellit curve

这曲线有点像鼓,绕在球上两头是开口的.

#http://www.mathcurve.com/courbes3d/satellite/satellite.shtml

vertices = 12000

t = from 0 to (40*PI)

r = 10
k = rand2(0.5, 10)
a = rand2(PI*0.1, PI*1.9)
 
x = r*(cos(a)*cos(t)*cos(k*t) - sin(t)*sin(k*t))
y = r*(cos(a)*sin(t)*cos(k*t) + cos(t)*sin(k*t))
z = r*sin(a)*cos(k*t)

(1)当上面代码中的k == 1时

#http://www.mathcurve.com/courbes3d/satellite/satellite.shtml
vertices = 12000
t = from 0 to (2*PI)
r = 10
k = 1
a = rand2(PI*0.1, PI*1.9)
 
x = r*(cos(a)*cos(t)*cos(k*t) - sin(t)*sin(k*t))
y = r*(cos(a)*sin(t)*cos(k*t) + cos(t)*sin(k*t))
z = r*sin(a)*cos(k*t)

生成一个帖在球上的伯努利双纽线

再将代码中的a = rand2(PI*0.1, PI*1.9)改为一个输入维度数据

vertices = D1:360 D2:100

u = from 0 to (PI) D1
v = from 0 to (2*PI) D2

r = 10
k = 1
 
x = r*(cos(v)*cos(u)*cos(k*u) - sin(u)*sin(k*u))
y = r*(cos(v)*sin(u)*cos(k*u) + cos(u)*sin(k*u))
z = r*sin(v)*cos(k*t)

这时生成一个曲面:

在这个曲面上,可以显示任意一个a值下生成的曲线.

(2)当上面代码中的k == 1时

2000
t = from 0 to (4*PI)
r = 10
k = 0.5
a = rand2(PI*0.1, PI*1.9)
x = r*(cos(a)*cos(t)*cos(k*t) - sin(t)*sin(k*t))
y = r*(cos(a)*sin(t)*cos(k*t) + cos(t)*sin(k*t))
z = r*sin(a)*cos(k*t)

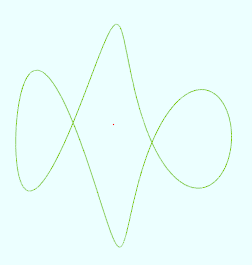
再将代码中的a = rand2(PI*0.1, PI*1.9)改为一个输入维度数据

vertices = D1:360 D2:100

u = from 0 to (2*PI) D1
v = from 0 to (2*PI) D2

r = 10
k = 0.5
 
x = r*(cos(v)*cos(u)*cos(k*u) - sin(u)*sin(k*u))
y = r*(cos(v)*sin(u)*cos(k*u) + cos(u)*sin(k*u))
z = r*sin(v)*cos(k*t)

这时生成一个曲面: