混沌与分形理论的关系密切,混沌中有时包容有分形,而分形中有时又孕育着混沌。分形更注重形态或几何特性,图形的描述。混沌偏重于数理的动力学及动力学与图形结合的多方位的描述和研究。分形则更看中有自相似性的系统。混沌涉及面似乎比分形更广,对所有的有序与无序,有序与有序现象都感兴趣。特别是混沌中的分叉,分支现象与分形关系最密切。分形可以是混沌研究中一种手段或方法。一般认为非线性,随机性,以及耗散性是出现分形结构的必要物理条件。 非线性是指运动方程中含有非线性项(迭代),状态演化(相空间轨迹)发生分支,是混沌的根本原因。
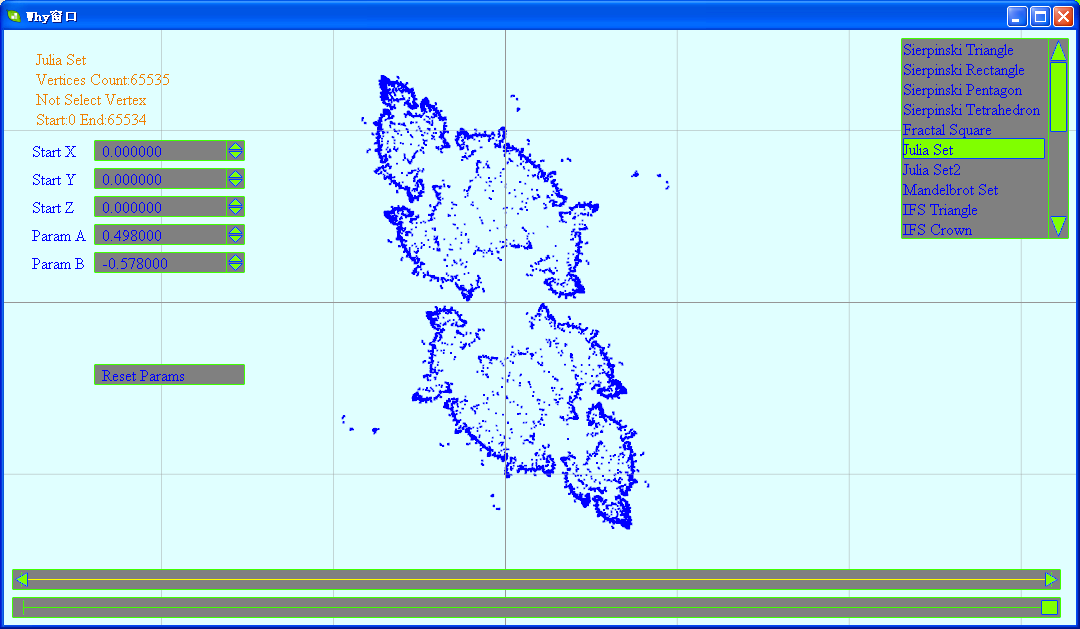
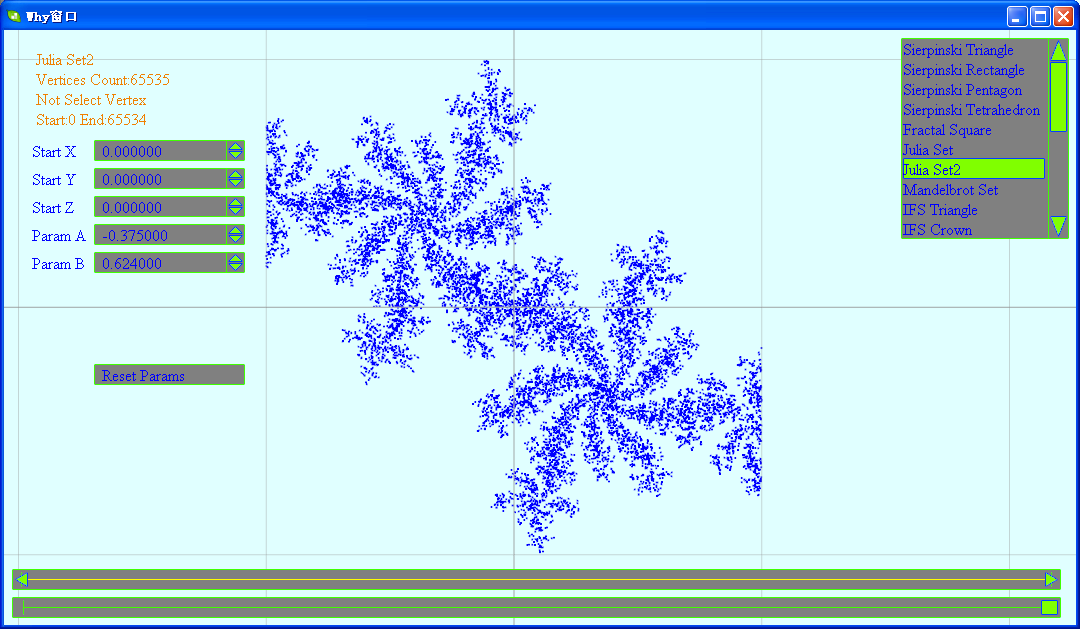
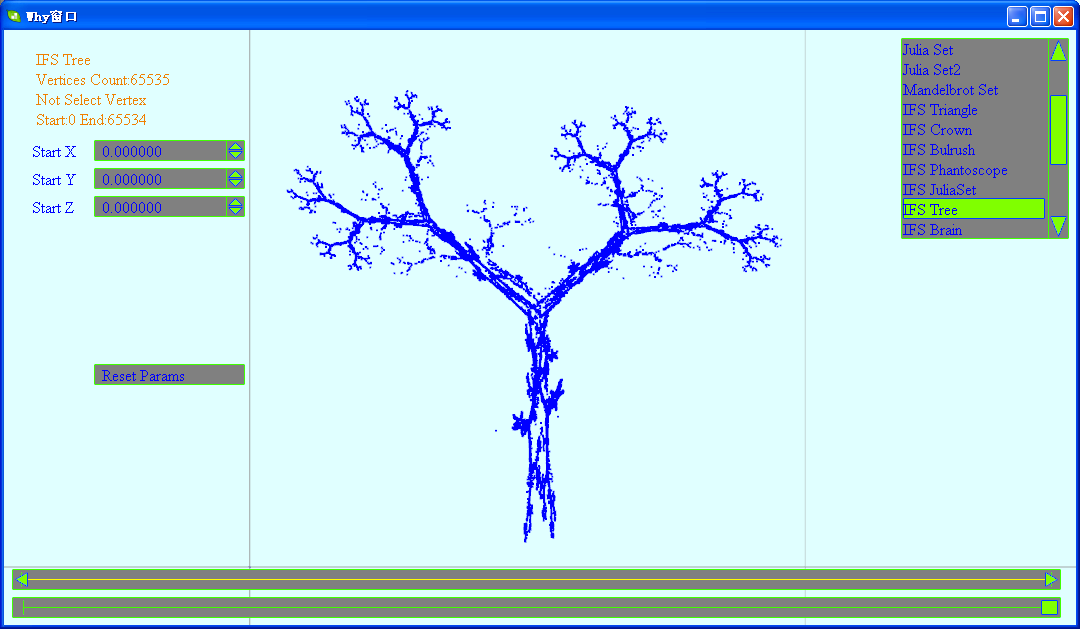
太理论的东西这里就不多说了,我将开辟新的一个版块,来讲下我在研究混沌分形时,实现的一些DEMO。在我之前的博客中,已有两个与混沌相关的版块混沌点集和混沌曲线。与前两个类似,这里也主要以DEMO的方式直观的介绍一些由混沌所生成的分形图形。DEMO中生成的图形都是以点集的方式存在,具体地讲就是:我将通过某种数学方程和参数设置,以得到65535个顶点坐标的位置。这65535个顶点的集合构成最终的分形图形。混沌是无序的,而分形又是有序的,在我的DEMO中可以看到如何将随机的数据生成有规律的图形。
(1)分形方程基类
首先介绍下我写的分形方程基类,之后所有的图形生成类都是它的派生类。
#define SET_GET_FLOAT_PROPERTY(name)
virtual void Set##name##(float v)
{
m_##name## = v;
}
float Get##name##() const
{
return m_##name##;
}
#define PI 3.14159265f
#define FRACTAL_RADIUS 5.0f
#define EPSILON 0.0001f
// --------------------------------------------------------------------------------------
class FractalEquation
{
public:
FractalEquation()
{
m_StartX = 0.0f;
m_StartY = 0.0f;
m_StartZ = 0.0f;
m_ParamA = 0.0f;
m_ParamB = 0.0f;
m_ParamC = 0.0f;
m_ParamD = 0.0f;
m_ParamE = 0.0f;
}
// 求迭代值
virtual void IterateValue(float x, float y, float z,
float& outX, float& outY, float& outZ) const = NULL;
// 计算点集的Y轴与X轴坐标
virtual void CalculatePoints(void* curveVerticesPtr, unsigned int stride, unsigned int count)
{
char* xPtr = (char*)curveVerticesPtr;
char* yPtr = (char*)curveVerticesPtr + sizeof(float);
char* zPtr = (char*)curveVerticesPtr + 2*sizeof(float);
float x, y, z;
float nx, ny, nz;
x = m_StartX;
y = m_StartY;
z = m_StartZ;
for (unsigned int i = 0; i < count; i++)
{
*(float*)xPtr = x;
*(float*)yPtr = y;
*(float*)zPtr = z;
IterateValue(x, y, z, nx, ny, nz);
x = nx;
y = ny;
z = nz;
xPtr += stride;
yPtr += stride;
zPtr += stride;
}
}
SET_GET_FLOAT_PROPERTY(StartX);
SET_GET_FLOAT_PROPERTY(StartY);
SET_GET_FLOAT_PROPERTY(StartZ);
SET_GET_FLOAT_PROPERTY(ParamA);
SET_GET_FLOAT_PROPERTY(ParamB);
SET_GET_FLOAT_PROPERTY(ParamC);
SET_GET_FLOAT_PROPERTY(ParamD);
SET_GET_FLOAT_PROPERTY(ParamE);
virtual bool IsValidParamA() const {return false;}
virtual bool IsValidParamB() const {return false;}
virtual bool IsValidParamC() const {return false;}
virtual bool IsValidParamD() const {return false;}
virtual bool IsValidParamE() const {return false;}
virtual bool Is3D() const {return false;}
protected:
float m_StartX;
float m_StartY;
float m_StartZ;
float m_ParamA;
float m_ParamB;
float m_ParamC;
float m_ParamD;
float m_ParamE;
};
其子类中需要实现如下函数:
// 求迭代值
virtual void IterateValue(float x, float y, float z, float& outX, float& outY, float& outZ) const = NULL;
其思想与混沌曲线中的相似,通过当前点位置生成下一个点的位置。外部需要调用CalculatePoints函数以生成所有顶点的位置坐标。
父类中有8个成员变量,这个可以在DEMO的UI界面上看到:
float m_StartX;
float m_StartY;
float m_StartZ;
float m_ParamA;
float m_ParamB;
float m_ParamC;
float m_ParamD;
float m_ParamE;
用于设置与方程相关的参数。
(2)DEMO介绍
ChaosFractal.exe和ChaosFractalFS.exe都可以启动程序。
DEMO启动后,窗体右上角的选择列表用于选择不同的分形图形。

窗体下方有两个滑动条,一个用于控制显示顶点的范围:
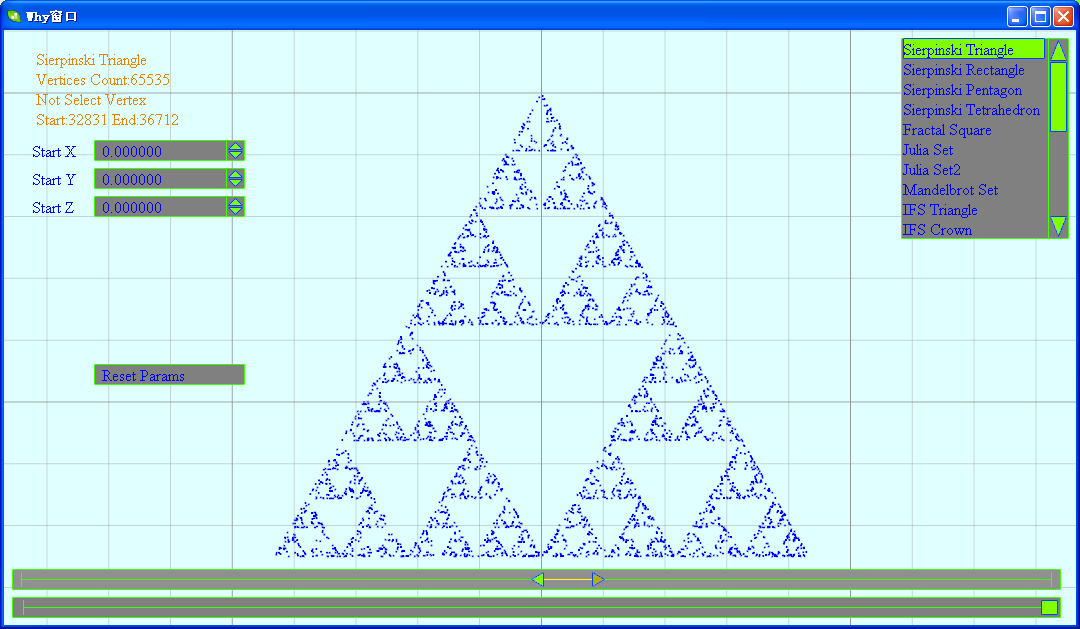
另一个用于显示指点顶点的位置:

窗体的左上角是显示当前状态的文字信息和设置相关参数的控件。
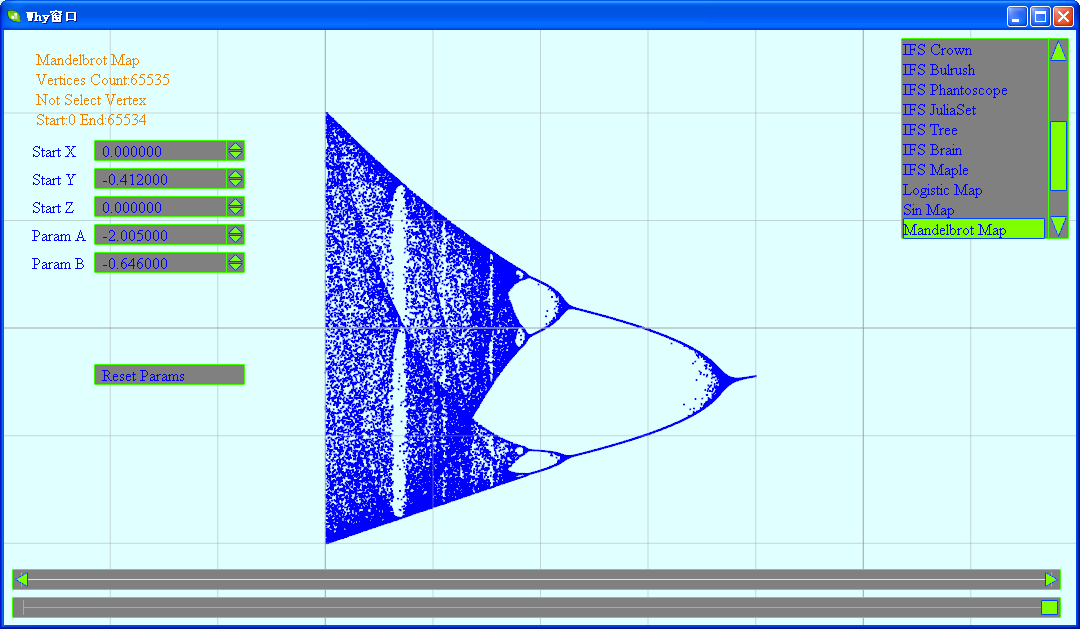
软件下载:http://files.cnblogs.com/WhyEngine/ChaosFractal.zip
(3)章节目录