POJ 3347 （思维题 + 简单计算）

题目： 传送门

题意：有 n 个正方形，倾斜 45 度按顺序放在 x 坐标轴上，然后那些正方形要尽可能的靠近，问排放好之后，你从上往下看，不会被遮住的正方形有哪些。

 

 

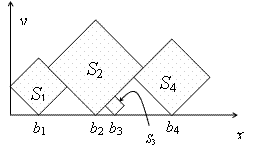
思路：我们可以算出每个正方形斜放的左右端点的 x 坐标。我们可以枚举前面已经放好的正方形，然后让当前这个正方形和它靠在一起算出当前这个点的左端点的 x 坐标，然后对这些 x 取最大值就是当前这个正方形的左端点的 x 坐标，然后右端点坐标就很容易得到了。我们对输入的边长扩大 sqrt(2) 倍这样就都是整数的运算了，就没有精度误差。

扩大后，正方形的对角线的长度就是 2len 了，然后算左端点的 x 坐标的公式就是， a[ j ].r - abs( a[ j ].len - len)，这里的 len 是输入的 len 不需要乘 sqrt(2) 因为，你乘 sqrt(2) 是倾斜 45 度时的长度，要把它变成水平的距离需要除 sqrt(2) 那一乘一除就相当于啥都没做。

最后暴力判断一下当前点是否会被覆盖到， 只有当其他正方形的边长大于你时，你才可能被覆盖。

#include <iostream>
#include <stdio.h>
#include <string.h>
#include <algorithm>
#include <queue>
#include <map>
#include <vector>
#include <set>
#include <string>
#include <math.h>
#define LL long long
#define mem(i, j) memset(i, j, sizeof(i))
#define rep(i, j, k) for(int i = j; i <= k; i++)
#define dep(i, j, k) for(int i = k; i >= j; i--)
#define pb push_back
#define make make_pair
#define INF 1e20
#define inf LLONG_MAX
#define PI acos(-1)
using namespace std;

const int N = 55;
pair < int, int > a[N];
int len[N];

int main() {
    int n;

    while(scanf("%d", &n) && n) {
        rep(i, 1, n) scanf("%d", &len[i]);

        rep(i, 1, n) {
            a[i].first = 0;
            rep(j, 1, i - 1)
                a[i].first = max(a[i].first, a[j].second - abs(len[i] - len[j]));
            a[i].second = a[i].first + 2 * len[i];
        }

        rep(i, 1, n) {
            rep(j, 1, i - 1) {
                if(len[j] > len[i] && a[j].second > a[i].first) a[i].first = a[j].second;
            }
            rep(j, i + 1, n) {
                if(len[j] > len[i] && a[j].first < a[i].second) a[i].second = a[j].first;
            }
        }

        bool flag = 0;
        rep(i, 1, n) {
            if(a[i].first >= a[i].second) continue;
            if(!flag) printf("%d", i), flag = 1;
            else printf(" %d", i);
        }
        puts("");
    }

    return 0;
}