题目
有N种物品和一个容量为V的背包，每种物品都有无限件可用。第i种物品的费用是c[i]，价值是w[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量，且价值总和最大。
完全背包按其思路仍然可以用一个二维数组来写出：
f[i][v]=max{f[i-1][v-k*c[i]]+k*w[i]|0<=k*c[i]<=v}
同样可以转换成一维数组来表示：
伪代码如下：
for i=1..N for v=0..V
f[v]=max{f[v],f[v-c[i]]+w[i]}
顺序！
想必大家看出了和01背包的区别，这里的内循环是顺序的，而01背包是逆序的。
现在关键的是考虑：为何完全背包可以这么写？
在次我们先来回忆下，01背包逆序的原因？是为了是max中的两项是前一状态值，这就对了。
那么这里，我们顺序写，这里的max中的两项当然就是当前状态的值了，为何？
因为每种背包都是无限的。当我们把i从1到N循环时，f[v]表示容量为v在前i种背包时所得的价值，这里我们要添加的不是前一个背包，而是当前背包。所以我们要考虑的当然是当前状态。
这里同样给大家一道题目：
题目：http://acm.hdu.edu.cn/showproblem.php?pid=1114
代码：http://www.cnblogs.com/William-xh/p/7339714.html
（分析代码也是学习算法的一种途径，有时并不一定要看算法分析，结合题目反而更容易理解。）
然后算完全背包时要注意：
- 求最大价值：要求恰好装满背包，那么在初始化时除了dp[0]为0其它dp[1..V]均设为-∞
- 求最小价值：要求恰好装满背包，那么在初始化时除了dp[0]为0其它dp[1..V]均设为∞
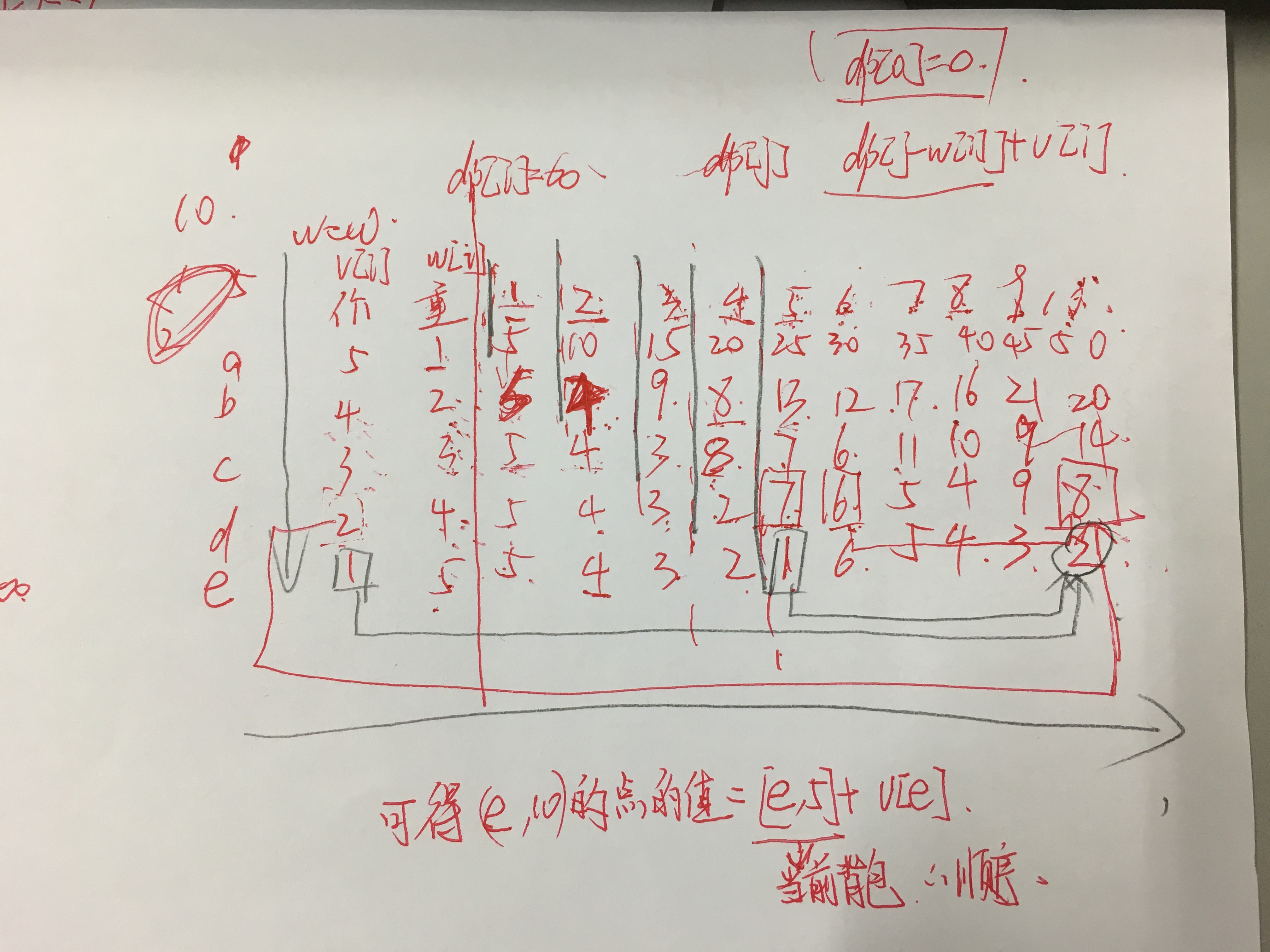
然后对于上面的那题，我在草稿纸上做了样例（大家最好自己手动去画画），这样大家可以更好地理解，为什么是顺序的。（因为我们需要知道的是当前背包的状态，而不是前一个）
