bzoj4173数学（欧拉函数）

解答：https://blog.csdn.net/popoqqq/article/details/46820313

　　　https://blog.csdn.net/zhhx2001/article/details/52300924

倒数第二行的拓展(借用某群提问的一个问题)：

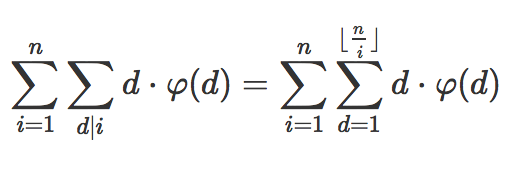
对于d*phi(d)，当d为k时，在左式，他出现在 i 为k,2k,3k...(n/k)*k  共出现n/k次，在右式，他出现在 n/i 为n/1,n/2...n/(n/k) 共出现n/k次，画个表格，每行就是每个 i 对应1,2,3...floor(n/i)，i 从1~n画出后就是一个逐渐缩减的三角形，每列对应一个d的值，每个d出现在 i 为floor(5/i)>=3的地方，终止在floor(5/i)=3的地方，所以每个d出现次数是 floor(n/i)！

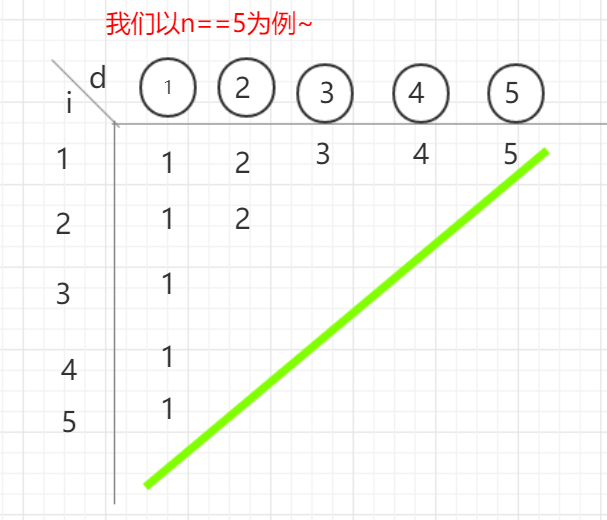而左式在图中的体现是把每个纵列d的每个安放位置调整一下，例如②，第一个2在i==1，第二个2调整到i==4,总出现次数不变（即看n中有几个大小为2的块）

这里d用两种不同的方式出现在这些个 i 中，分析第一种有n/k个值能d|i 时，第二种就是把这个方式解释一下 ~~~

而等号右边换成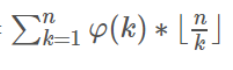同样成立，证明更简单了，就是参数为k时出现n/k次！！！

第一个等式用莫比乌斯反演列出f(1),f(2)...f(n)那些个等式，就很容易发现F(n)=n

小总结：模‘%’  整除‘|’ 这些抽象符号尽量化简成+-*/ 的形式！！！

ac代码：

#include<bits/stdc++.h>
#define per(i,a,b) for(int i=a;i<=b;i++)
#define mod 998244353//注意mod最好define，不要定义类型，否则需要ll的时候会错，不过呢，ll的时候int也会变成ll把
using namespace std;
typedef long long ll;
const int inf =0x3f3f3f3f;
const double eps=1e-8;
//#define siz 1000005
ll read()
{
    ll res=0,f=1;
    char ch=getchar();
    while(ch<'1'||ch>'9'){f=ch=='-'?-1:1;ch=getchar();}
    while(ch>'1'&&ch<'9'){res=res*10+ch-'0';ch=getchar();}
    return res*f;
}
ll n,m;
ll phi(ll n)
{
    ll i,re=n;
    for(i=2;i*i<=n;i++){
        if(n%i==0){
            re=re/i*(i-1);//注意先出后乘，如果先乘可能会超出数据范围
            while(n%i==0){n/=i;}//n除完素因子后为1
        }
    }
    if(n!=1){re=re/n*(n-1);}
    return re;
}
int main()
{
    scanf("%lld%lld",&n,&m);
    printf("%lld
",phi(n)%mod*(phi(m)%mod)%mod*(n%mod)%mod*(m%mod)%mod);
    return 0;
}