[BZOJ1500]维修数列

Problem

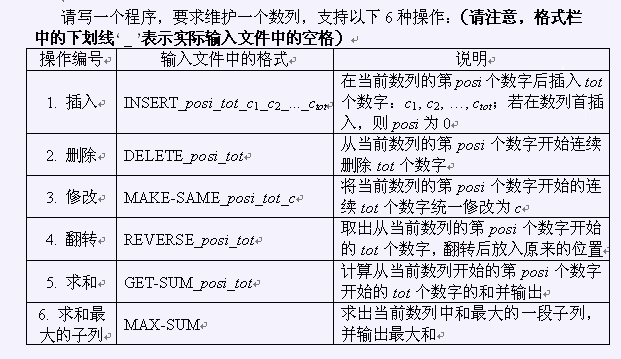
Solution

Splay模板题
要记录从左往右的最大和，从右往左的最大和，整个区间内的最大和

Notice

注意0的大坑。

Code

#include<cmath>
#include<queue>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define sqz main
#define ll long long
#define reg register int
#define rep(i, a, b) for (reg i = a; i <= b; i++)
#define per(i, a, b) for (reg i = a; i >= b; i--)
#define travel(i, u) for (reg i = head[u]; i; i = edge[i].next)
const int INF = 1e9, N = 500000;
const double eps = 1e-6, phi = acos(-1.0);
ll mod(ll a, ll b) {if (a >= b || a < 0) a %= b; if (a < 0) a += b; return a;}
ll read(){ ll x = 0; int zf = 1; char ch; while (ch != '-' && (ch < '0' || ch > '9')) ch = getchar();
if (ch == '-') zf = -1, ch = getchar(); while (ch >= '0' && ch <= '9') x = x * 10 + ch - '0', ch = getchar(); return x * zf;}
void write(ll y) { if (y < 0) putchar('-'), y = -y; if (y > 9) write(y / 10); putchar(y % 10 + '0');}
queue<int> Q;
int root, num, tx, X[N + 5];
struct node
{
    int val[N + 5], Max[N + 5], Left[N + 5], Right[N + 5], son[2][N + 5], parent[N + 5], Sum[N + 5], Size[N + 5], rev[N + 5], cover[N + 5];
    void up(int u)
    {
        if (!u) return;
        Left[u] = max(Left[son[0][u]], Sum[son[0][u]] + val[u] + max(Left[son[1][u]], 0));
        Right[u] = max(Right[son[1][u]], Sum[son[1][u]] + val[u] + max(Right[son[0][u]], 0));
        Max[u] = max(max(Max[son[0][u]], Max[son[1][u]]), max(0, Right[son[0][u]]) + val[u] + max(0, Left[son[1][u]]));
        Sum[u] = Sum[son[0][u]] + Sum[son[1][u]] + val[u];
        Size[u] = Size[son[0][u]] + Size[son[1][u]] + 1;
    }
    void Reverse(int x)
    {
        if (!x) return;
        swap(son[0][x], son[1][x]);
        swap(Left[x], Right[x]);
        rev[x] ^= 1;
    }
    void Recover(int u, int z)
    {
        if (!u) return;
        val[u] = cover[u] = z;
        Sum[u] = Size[u] * z;
        Left[u] = Right[u] = Max[u] = max(z, Sum[u]);
    }
    void down(int u)
    {
        if (!u) return;
        if (rev[u])
        {
            Reverse(son[0][u]), Reverse(son[1][u]);
            rev[u] = 0;
        }
        if (cover[u] != -INF)
        {
            Recover(son[0][u], cover[u]);
            Recover(son[1][u], cover[u]);
            cover[u] = -INF;
        }
    }

    int pick()
    {
        if (!Q.empty())
        {
            int t = Q.front();
            Q.pop();
            return t;
        }
        else return ++num;
    }
    int Find(int u, int t)
    {
        down(u);
        if (t == Size[son[0][u]] + 1) return u;
        else if (t <= Size[son[0][u]]) return Find(son[0][u], t);
        else return Find(son[1][u], t - Size[son[0][u]] - 1);
    }
	void Newnode(int &u, int from, int v)
	{
	    u = pick();
	    parent[u] = from, val[u] = v, Size[u] = 1;
	    Left[u] = Right[u] = Max[u] = val[u];
	    cover[u] = -INF, rev[u] = 0;
	}

	void Rotate(int x, int &rt)
	{
		int y = parent[x], z = parent[y];
		int l = (son[1][y] == x), r = 1 - l;
		if (y == rt) rt = x;
		else if (son[0][z] == y) son[0][z] = x;
		else son[1][z] = x;
		parent[x] = z;
		parent[son[r][x]] = y, son[l][y] = son[r][x];
		parent[y] = x, son[r][x] = y;
		up(y), up(x);
	}
	void Splay(int x, int &rt)
	{
		while (x != rt)
		{
			int y = parent[x], z = parent[y];
			if (y != rt)
			{
				if ((son[0][z] == y) ^ (son[0][y] == x))
					Rotate(x, rt);
				else Rotate(y, rt);
			}
			Rotate(x, rt);
		}
	}

    void Split(int l, int r)
    {
        int x = Find(root, l - 1 + 1), y = Find(root, r + 1 + 1);
        Splay(x, root), Splay(y, son[1][root]);
    }
	void Build(int &u, int l, int r, int from)
	{
	    int mid = (l + r) >> 1;
	    Newnode(u, from, X[mid]);
	    if (l < mid) Build(son[0][u], l, mid - 1, u);
	    if (r > mid) Build(son[1][u], mid + 1, r, u);
	    up(u);
	}
	void Insert(int x, int y)
	{
	    Split(x + 1, x);
	    Build(son[0][son[1][root]], 1, y, son[1][root]);
	    up(son[1][root]), up(root);
	}
    void Delete(int &u)
    {
        if (!u) return;
        Q.push(u);
        parent[u] = 0;
        Delete(son[0][u]), Delete(son[1][u]);
        Left[u] = Right[u] = Max[u] = -INF, Sum[u] = 0;
        u = 0;
    }
}Splay_tree;

int sqz()
{
    int n = read(), m = read();
    rep(i, 1, n) X[i] = read();
    Splay_tree.Max[0] = Splay_tree.Left[0] = Splay_tree.Right[0] = -INF, Splay_tree.Sum[0] = 0;
    X[0] = X[n + 1] = 0; tx = n;
    Splay_tree.Build(root, 0, n + 1, 0);
    char st[15];
    int x, y, z;
    while (m--)
    {
        scanf("%s", st);
        switch (st[0])
        {
            case 'I' : x = read(), y = read(); rep(i, 1, y) X[i] = read();
                     tx += y, Splay_tree.Insert(x, y); break;
            case 'D' : x = read(), y = read(), Splay_tree.Split(x, x + y - 1), tx -= y;
                    Splay_tree.Delete(Splay_tree.son[0][Splay_tree.son[1][root]]); Splay_tree.up(Splay_tree.son[1][root]), Splay_tree.up(root); break;
            case 'M' :
                        if (st[2] == 'K')
                        {
                            x = read(), y = read(), z = read();
                            Splay_tree.Split(x, x + y - 1);
                            Splay_tree.Recover(Splay_tree.son[0][Splay_tree.son[1][root]], z);
                        }
                        else
                        {
                            Splay_tree.Split(1, tx);
                            printf("%d
", Splay_tree.Max[Splay_tree.son[0][Splay_tree.son[1][root]]]);
                        }
                        break;
            case 'R' : x = read(), y = read(); Splay_tree.Split(x, x + y - 1), Splay_tree.Reverse(Splay_tree.son[0][Splay_tree.son[1][root]]); break;
            case 'G' : x = read(), y = read(), Splay_tree.Split(x, x + y - 1);
                    printf("%d
", Splay_tree.Sum[Splay_tree.son[0][Splay_tree.son[1][root]]]); break;
        }
    }
    return 0;
}