数据结构之树

线索二叉树

/**
 * 线索二叉树：普通二叉树的遍历操作，需要用到栈来实现递归操作，而线索二叉树，因为其保存了前驱和后继，在遍历操作中不需
 * 要使用栈来递归，直接根据后继一直遍历，直到回到初始头结点，对比普通二叉树避免了频繁的入栈出栈操作，故在时间和空间上
 * 都比较节省
 * @author HP
 *
 */
public class ListOfBiTree {
    
    class node{
        
        int data;
        int leftTag;  // 若为 0, leftChild 保存左子树，若为 1, leftChild 保存前驱
        int rightTag; // 若为 0, rightChild 保存右子树，若为 1, righrChild 保存后继
        node leftChild;
        node rightChild;
    }
    
    node lastNode = new node();
    
    public void traval(node ListTree) {
        if (ListTree != null) {
            node root = ListTree.leftChild;
            // 遍历结束时回到头结点
            while (root != ListTree) {
                // 找到最左边的节点
                while (root.leftTag == 0) {
                    root = root.leftChild;
                }
                System.out.print(root.data);
                // 利用找到的起始节点开始根据后继遍历
                while (root.rightTag == 1 && root.rightChild != ListTree) {
                    root = root.rightChild;
                    System.out.print(root.data);
                }
                
                root = root.rightChild;
            }
        }
    }
    
    // 建立线索二叉树，tree的初始化只需像普通二叉树建立即可（tag初始化为0），在此省略tree的初始化代码
    public node creatListOfBiTee(node tree, node head) {
        
        if (tree != null && head != null) {
            
            head.leftChild = tree;
            lastNode = head; // 上一次遍历的节点初始化为头结点
            InitTree(tree);
            
            /*
             * 最后一个节点的后继指回头结点（其实最后一个节点是没有后继节点的，为了满足线索二叉树定义及方便遍历
             * 故指回了头结点）
             */
            lastNode.rightChild = head;
            lastNode.rightTag = 1;
            /*
             *  线索二叉树初始化完，改变头结点的后继指向根节点（初始化的时候为了统一操作，是把头结点的后继指向了
             *  最左边的节点）
             */
            head.rightChild = tree;
        }
        
        return head;
    }
    
    public void InitTree(node root) {
        
        if (root != null) {
            
            InitTree(root.leftChild);  // 递归对左子树进行初始化
            
            
            if (root.leftChild == null) {
                // 左子树为 null，说明已到叶子节点，将该叶子节点的前驱指向 上一次遍历到的节点
                root.leftTag = 1;
                root.leftChild = lastNode;
            }else {
                root.leftTag = 0; // 0 代表该节点有左子树
            }
            
            // 由于我们无法预知当前节点的后继（因为还没遍历到），但我们知道上一个节点的后继就是当前节点
            if (lastNode.rightChild == null) {
                lastNode.rightTag = 1;
                lastNode.rightChild = root;
            }else {
                lastNode.rightTag = 0;
            }
            // 当前节点的 左右孩子域更新完，所以当前节点在接下来的操作就是作为上一次操作的节点了
            lastNode = root;
            
            InitTree(root.rightChild); // 递归遍历右子树
            
        }
    }
}

哈夫曼树

　　数据结构类型如图

　　哈夫曼树的建立还是比较容易的，每次取权最小的两个根节点构成一棵二叉树，新生成的根加入根节点集合并删除取出的两个根节点，修改这两个节点的双亲域。因为一开始都是n个度为0的根节点，所以如果形成哈夫曼树节点数就为 2n-1 （由二叉树性质n0 = n2 + 1，哈夫曼树是由度为0或2的节点组成的 n + （n-1） = 2n - 1），然后就可以开 2n-1的数组来存这些节点，前n个元素存原始n个节点，后n-1个存每次生成的结果（当然也可以用两条链表来操作，一条是原始链，一条结果链）。具体代码就不上了。哈夫曼树一般用在编码，在得到哈夫曼树后怎么编码？对，每个原始根节点进行遍历，如果是双亲的左孩子，把0压栈，右孩子把1压栈，直到双亲域为空，然后弹栈得出的结果即为编码。

二叉搜索树

　　它或者是一棵空树，或者是具有下列性质的二叉树： 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值； 它的左、右子树也分别为二叉排序（搜索）树，如下图：

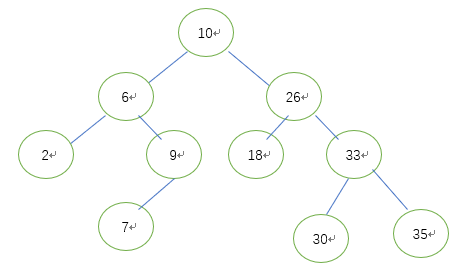
　　建树过程就是每次进行节点插入的时候先和根节点比较，小于根节点进入左子树，如果左子树为null则直接插入，否则进入左子树做递归；大于则进入右子树，如果右子树为null则直接插入，否则进入右子树做递归。

　　贴一道题目

　　输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则输出Yes,否则输出No。假设输入的数组的任意 两个数字都互不相同。

　　

public boolean VerifySquenceOfBST(int[] sequence) {
        int n = sequence.length;
        if (n == 0) {
            return false;
        }
        if (n == 1 || n == 2) {
            return true;
        }
        if (is(sequence, 0, sequence.length - 1)) {
            return true;
        }
        return false;
    }

    public boolean is(int[] back, int start, int end) {
        
        if (end <= start) {
            // 遍历到尾只剩一个元素
            return true;
        }
        
        int i = start;
        /* 
         * 因为后续遍历的最后一个元素一定是根节点，又因为是二叉搜索树，前面的元素一定是左子树和右子树，左子树的所
         * 有节点一定小于根节点，右子树的所有节点一定大于根节点，通过以下循环找出左右子树分割点
         */
        for (; i < end; i++) {
            if (back[i] > back[end]) {
                break;
            }
        }
        for (int j = i; j < end; j++) {
            // 如果是后续遍历的结果，从 j 开始的后续节点为右子树节点，所有节点值要大于根，否则说明并不是后续遍
            // 历结果
            if (back[j] < back[end]) {
                return false;
            }
        }
        
        return is(back, 0, i - 1) && is(back, i, end - 1);
    }