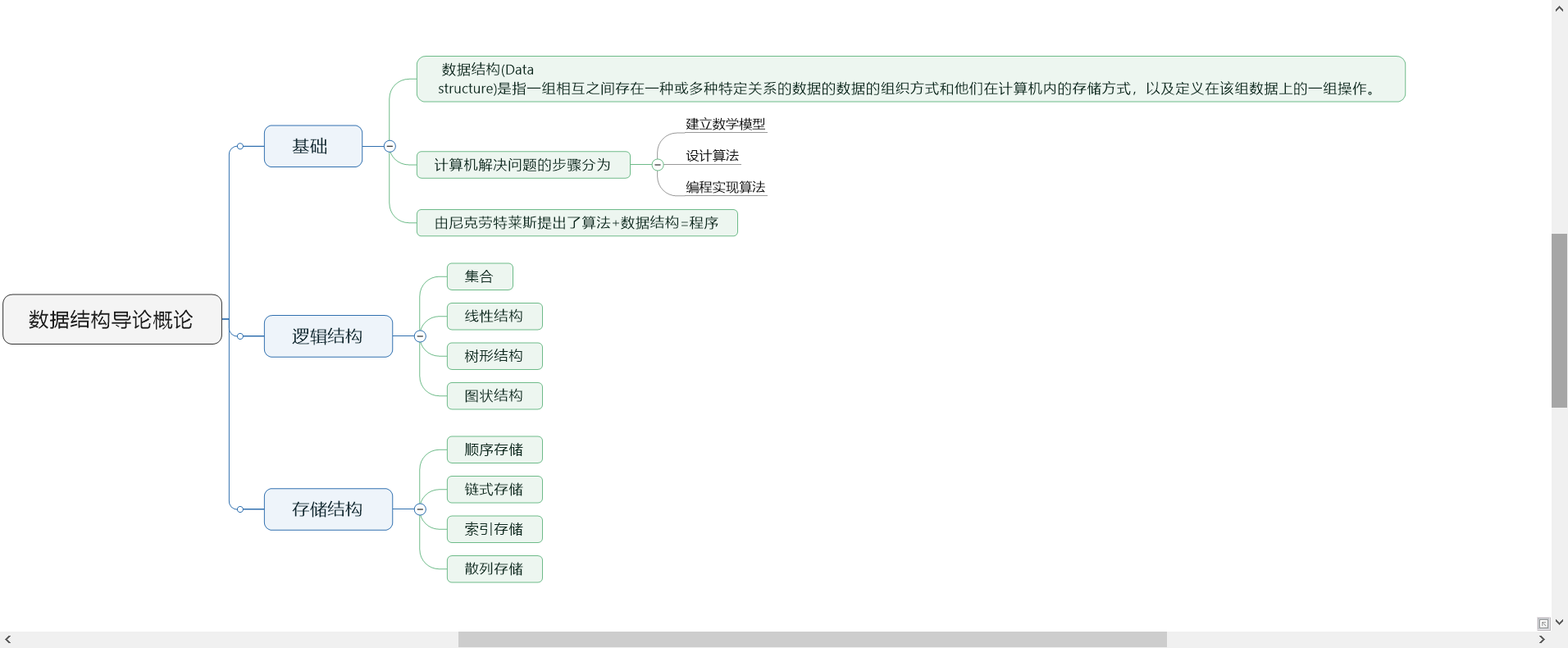
通过上一章,https://www.cnblogs.com/X404/p/11984707.html中可以知道数据结构分为
1.逻辑结构 包含:
1)集合
2)线性结构
3)树形结构
4)图结构
2.存储结构
1)顺序存储
2)链式存储
3)索引存储
4)散列存储
以上也是重点需要进行了解的,
废话不多说,跟着第一章走,算法的设计应该满足一下:
1.正确性 :保证是否正确
2.易读性:是否简单易懂
3.健壮性:在输入非法数据时,是否出错
4.时空性:分析 时间复杂度 和空间复杂度 提高算法效率(重点)
选择最优算法的2各度量:
时间复杂度:算法运行时所需要的总步数(从开始运行到打断点)
空间复杂度:算法执行时所占的存储空间(运行后存储空间的大小)
合理地选择一种或者几种操作作为“标准操作”
确定每个算法执行了多少次标准操作,并将此次数规定位该算法的计算量
时间复杂度的确定计算量:
算法的最坏情况时间复杂度:算法在所有输入下的计算量的最大值为计算量
(最坏时间复杂度是相当于运动会的接力棒,从开始到结束总共用的时间被称为最坏时间复杂度)
算法的平均情况时间复杂度:算法在所有输入下的计算量的加权平均值算法的计算量
(平均情况时间复杂度,仍可以用运动会接力来说,在一段时间内,所平均的值称为 加权平均)
最坏情况时间复杂度和平均情况复杂度统称为时间复杂度
最坏情况时间复杂度+加权平均情况复杂度《= 时间复杂度 (最坏和加权是包含在时间复杂度内的)
void max(int a,b,c,d) {a*=d;b*=d,c*=d; if (a>b)x=a; else x=b; if (c>x)x=c; printf("%d ",x);} /*有时间可以拿笔算一下这个最坏时间复杂度是多少?*/
常见的时间复杂度按数量级递增排列一次为:
常数 O(1):无论执行多少行没有循环等复杂结构的都是O(1)
int i,j;
i=2;
j=3 i++; j++
i=i+j;
对数阶O(long2n):
1 int a; 2 while(a<n){ 3 a=a*2; 4 }
在while循环里面,每次都将 a 乘以 2,乘完之后,a距离 n 就越来越近了。我们试着求解一下,假设循环x次之后,a 就大于 2 了,此时这个循环就退出了,也就是说 2 的 x 次方等于 n,那么 x = log2n
也就是说当循环 log2n 后代码就结束。因此这个代码的时间复杂度为:O(logn)
线性阶O(n):
1 int i; 2 for(i=0,i<n,i++){ 3 printf("*******");}
这段代码,for循环里面的代码会执行n遍,因此它消耗的时间是随着n的变化而变化的,因此这类代码都可以用O(n)来表示它的时间复杂度。
线性对数阶 O(nlong2n):
线性对数阶O(nlogN) 其实非常容易理解,将时间复杂度为O(logn)的代码循环N遍的话,那么它的时间复杂度就是 n * O(logN),也就是了O(nlogN)。
1 for(i=1,i<n,i++){ 2 j=1; 3 while(j<n){ 4 j=j*2;}}
平方阶O(n2),
多项式阶OnC),
指数阶O(Cn)
我们可以将时间复杂度几位输入数据规模n的函数,若求解问题需要执行n2次操作,则记作O(n2)
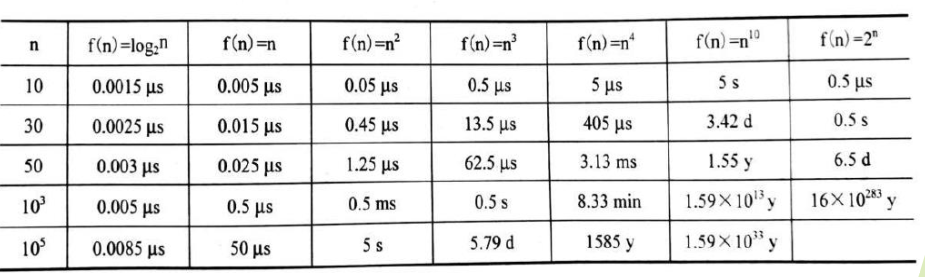
时间复杂度与时间的关系
空间复杂度:
是一个算法在运行过程中临时占用存储空间大小的量度。
一个算法在执行期间所需要的存储空间量包括以下部分:
程序代码所占用的空间;
输入数据所占用的空间;
辅助变量所占用的空间;