弗洛伊德算法
维基百科，自由的百科全书
Floyd-Warshall算法（Floyd-Warshall algorithm）是解决任意两点间的最短路径的一种算法，可以正确处理有向图或负权的最短路径问题，同时也被用于计算有向图的传递闭包。
Floyd-Warshall算法的时间复杂度为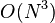
，空间复杂度为
。
[编辑]原理
Floyd-Warshall算法的原理是动态规划。
设
为从
到
的只以
集合中的节点为中间节点的最短路径的长度。
- 若最短路径经过点k，则
； - 若最短路径不经过点k，则
。
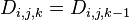因此，
。
在实际算法中，为了节约空间，可以直接在原来空间上进行迭代，这样空间可降至二维。（见下面的算法描述）
[编辑]算法描述
Floyd-Warshall算法的描述如下：
for k ← 1 to n do
for i ← 1 to n do
for j ← 1 to n do
if (
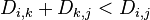
) then
←
;
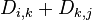
其中表示由点到点的代价，当为 ∞ 表示两点之间没有任何连接。
[编辑]请参阅
|
||||||||||||||||||||