题目链接
题目描述

解题思路
1.观察法
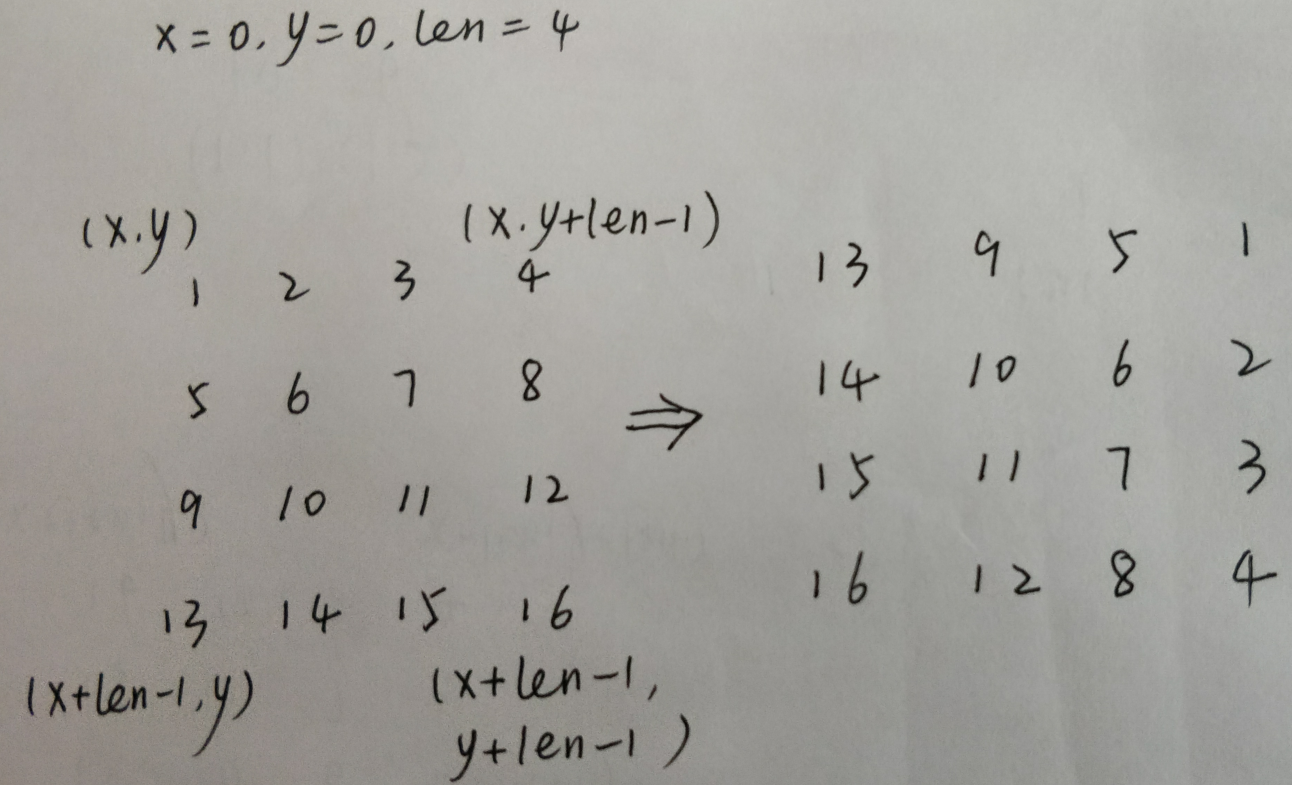
利用变量x,y代替坐标,根据题目要求去发现坐标之间的关系,尽量不要直接用确定的数字来表示坐标,这样当情况复杂的时候很容易搞混。
我们可以发现矩阵的旋转可以转变为每一圈每个元素的的旋转,例如1->4->16->13转变为13->1->4->16,2->8->15->9变为9-2-8-15,这旋转的原理就和一维数组一样:将每一位数字都向后移动一位,从后向前遍历即可。
循环终止的条件为达到整个矩阵的最内层。
2.观察法
先以对角线为轴进行翻转,再对每行左右翻转即可。
如下图,先以对角线 [1, 5, 9] 为轴进行翻转:

于是数组变成了:
[1,4,7]
[2,5,8]
[3,6,9]
再对每一行以中点进行翻转,就得到了最终结果:
[7,4,1]
[8,5,2]
[9,6,3]
AC代码
class Solution {
public void rotate(int[][] matrix) {
int x = 0;
int y = 0;
int len = matrix.length;
int time = 0;
//matrix.length / 2为矩阵的层数
while(time < matrix.length / 2){
//原理类似一维数组向后移动一位,只不过这是二维,坐标处理复杂一些。
for(int i = 0; i < len - 1; i++){
int startValue = matrix[x][y+i];
matrix[x][y+i] = matrix[x+len-1-i][y];
matrix[x+len-1-i][y] = matrix[x+len-1][y+len-1-i];
matrix[x+len-1][y+len-1-i] = matrix[x+i][y+len-1];
matrix[x+i][y+len-1] = startValue;
}
time++;
x++;
y++;
len -= 2;
}
}
}
2.观察法
class Solution {
public void rotate(int[][] matrix) {
int n = matrix.length;
// 先以对角线为轴进行翻转
for (int i = 0; i < n - 1; i++) {
for (int j = i + 1; j < n; j++) {
int tmp = matrix[i][j];
matrix[i][j] = matrix[j][i];
matrix[j][i] = tmp;
}
}
// 再对每一行以中点进行翻转
int mid = n >> 1;
for (int i = 0; i < n; i++) {
for (int j = 0; j < mid; j++) {
int tmp = matrix[i][j];
matrix[i][j] = matrix[i][n - 1 - j];
matrix[i][n - 1 - j] = tmp;
}
}
}
}
补充题
本题是「旋转二维数组」,如果是「旋转一维数组」呢?
题目:给定一个长度为 n 的一维数组,将前 k 个数移动到末尾。要求 原地 操作,该如何实现?
样例:
输入: 1, 2, 3, 4, 5, 6, 7
输出: 4, 5, 6, 7, 1, 2, 3
- 前 k 个原地翻转
- 后 n - k 个原地翻转
- 整体原地翻转
1, 2, 3, 4, 5, 6, 7
前 k 个原地翻转:
3, 2, 1, 4, 5, 6, 7
后 n - k 个原地翻转:
3, 2, 1, 7, 6, 5, 4
整体原地翻转:
4, 5, 6, 7, 1, 2, 3