Codeforces Round #272 (Div. 1) Problem C. Dreamoon and Strings

C. Dreamoon and Strings

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Dreamoon has a string s and a pattern string p. He first removes exactly x characters from s obtaining string s' as a result. Then he calculates 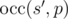 that is defined as the maximal number of non-overlapping substrings equal to p that can be found in s'. He wants to make this number as big as possible.

More formally, let's define 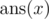 as maximum value of  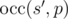over all s' that can be obtained by removing exactly x characters froms. Dreamoon wants to know  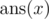for all x from 0 to |s| where |s| denotes the length of string s.

Input

The first line of the input contains the string s (1 ≤ |s| ≤ 2 000).

The second line of the input contains the string p (1 ≤ |p| ≤ 500).

Both strings will only consist of lower case English letters.

Output

Print |s| + 1 space-separated integers in a single line representing the 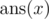 for all x from 0 to |s|.

Sample test(s)

input

aaaaa
aa

output

2 2 1 1 0 0

input

axbaxxb
ab

output

0 1 1 2 1 1 0 0

Note

For the first sample, the corresponding optimal values of s' after removal 0 through |s| = 5 characters from s are {"aaaaa", "aaaa","aaa", "aa", "a", ""}.

For the second sample, possible corresponding optimal values of s' are {"axbaxxb", "abaxxb", "axbab", "abab", "aba", "ab","a", ""}.

题解报告：

几天后补上

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <vector>
#include <stack>
#include <map>
#include <set>
#include <queue>
#include <iomanip>
#include <string>
#include <ctime>
#include <list>
#include <bitset>
typedef unsigned char byte;
#define pb push_back
#define input_fast std::ios::sync_with_stdio(false);std::cin.tie(0)
#define local freopen("in.txt","r",stdin)
#define pi acos(-1)

using namespace std;
const int maxn = 2e3 + 50;
char s[maxn],p[maxn];
int errorcode,ans[maxn];

inline void updata(int & x ,int v){x=min(x,v);}

int main(int argc,char *argv[])
{
    scanf("%s%s",s+1,p+1);
    int l1 = strlen(s+1),l2=strlen(p+1);
    int dp[l1+3][l2+3][l1/l2+2],shang=l1/l2+1;
    memset(dp,0x3f,sizeof(dp));errorcode=dp[0][0][0];dp[0][0][0]=0;memset(ans,0,sizeof(ans));
    for(int i = 0 ; i < l1 ; ++ i)
        for(int j = 0 ; j < l2 ; ++ j)
            for(int k = 0 ; k <= shang ; ++ k)
                if(dp[i][j][k]!=errorcode)
                {
                    if(j==0) updata(dp[i+1][j][k],dp[i][j][k]);
                    else updata(dp[i+1][j][k],dp[i][j][k]+1);
                    if(s[i+1]==p[j+1])
                    {
                        if(j==l2-1)
                            updata(dp[i+1][0][k+1],dp[i][j][k]);
                        else
                            updata(dp[i+1][j+1][k],dp[i][j][k]);
                    }
                    else
                    {
                        updata(dp[i+1][0][k],dp[i][j][k]);
                    }
                }
    for(int j = 0 ; j <= l2 ; ++ j)
        for(int k = 0 ; k <= shang ; ++ k)
            if(dp[l1][j][k] != errorcode)
             {
                int v = dp[l1][j][k];
                ans[v] = max(ans[v],k);
             }
    for(int i = 0 ; i <= l1 ; ++ i)
        if(ans[i])
        {
            for(int j = i + 1 ; j <= l1 ; ++ j)
                ans[j]=max(ans[j],min((l1-j)/l2,ans[i]));
        }
    printf("%d",ans[0]);
    for(int i = 1 ; i <= l1 ; ++ i) printf(" %d",ans[i]);printf("
");
    return 0;
}