前面几篇介绍的选择排序、插入排序、冒泡排序等都是非常简单非常基础的排序算法,都是用了两个for循环,时间复杂度是平方级别的。本篇介绍一个比前面稍微复杂一点的算法:归并排序。归并排序算法里面的归并思想和递归方法是值得我们学习的,归并的过程往往伴随着递归,其他很多地方都会用这两种方法,比如前面一篇《剑指offer题目系列三》中第12题“合并两个排序的链表”就用到这两种思想方法。
归并的过程
对于两个独立的数组来说,是将两个有序的数组合并到一个数组中,使合并后的数组依然有序。对于一个数组来说,可以先将其划分为两部分,先使其各部分都有序,然后合并成一个有序数组。具体操作时,先定义两个指针,分别指向两个数组中的元素,用于遍历数组,然后新建一个数组用于存储合并后的元素。
归并排序中,假设p、q、mid分别指向数组arr[]的第一个元素、最后一个元素、中间元素的索引位置,将数组arr[]划分成两半:arr[p~mid]、arr[mid+1~q],然后将两个子数组中的元素归并。还可以将两个子数组再次划分为更小的子数组,归并更小的子数组……以此类推,直到子数组长度为1,然后依次归并。归并时,有4个判定条件:如果左半块元素遍历完毕,则直接将右半块剩余元素放入数组中;如果右半块元素遍历完毕,则直接将左半块剩余元素放入数组中;如果左半块当前元素小于右半块当前元素,则左半块当前元素放入数组;反之,右半块当前元素放入数组。
下面以长度为8的数组为例,说明归并的具体过程。设原数组为int arr[] = {1,3,5,7,2,4,6,8};,新建一个辅助数组aux[]用于临时存储数组中的元素,先将原数组中的元素复制到辅助数组中,再把归并的结果放回原数组中。初始i、j分别指向辅助数组前半部分、后半部分子数组的第一个元素位置,然后慢慢移动遍历两个数组。红色元素代表每一趟 i、j 两个指针指向的两个子数组的元素位置,灰色元素代表已遍历完的元素,黑色加粗元素代表还未遍历的元素。
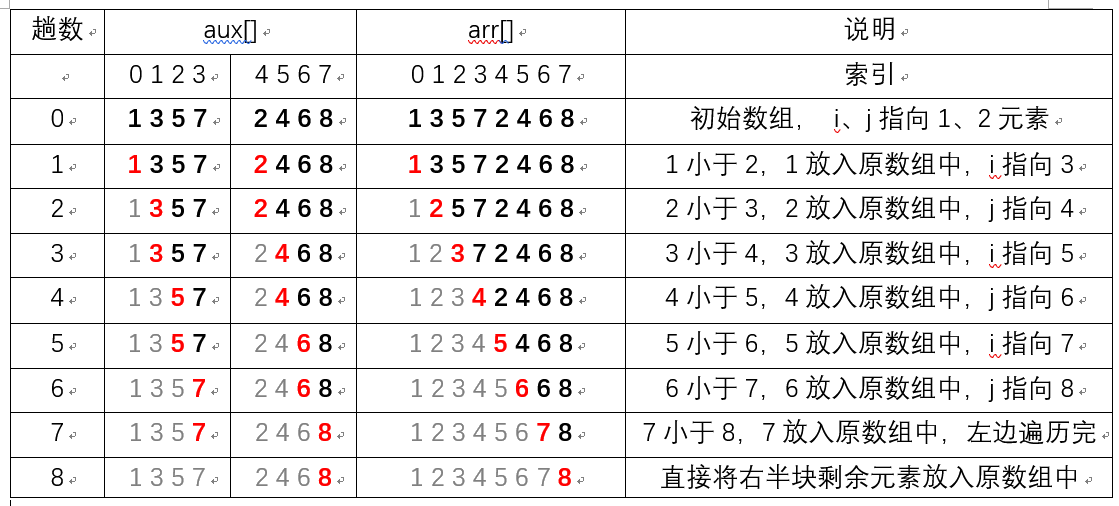
归并过程的代码:
public static void merge(int[] arr,int[] aux,int p,int mid,int q){ for(int k=p;k<=q;k++){ //先复制到辅助数组中 aux[k] = arr[k]; } int i=p,j=mid+1; //i、j指向辅助数组左右半块指针,从起始位置开始 for(int k=p;k<=q;k++){ //k指向原数组arr[],根据i、j指针位置判断左右半块是否遍历完 if(i > mid) arr[k] = aux[j++]; //左半块遍历完 else if(j>q) arr[k] = aux[i++]; //右半块遍历完 else if(aux[j]>aux[i]) arr[k] = aux[i++]; else arr[k] = aux[j++]; } }
下面介绍递归排序的两种方式:自顶向下归并排序和自底向上归并排序,两种方式都会用到上面的归并代码。
自顶向下归并
自顶向下归并是一种基于递归方式的归并,也是算法设计中“分治思想”的典型用法。它将一个大问题分割成一个个小问题,分别解决小问题,然后用所有小问题的答案来解决整个大问题。如果能将两个子数组排序,就能通过归并两个子数组使整个数组排序。自顶向下归并每次先将数组的左半部分排序,然后将右半部分排序,通过归并左右两部分使整个数组排序。详细过程见下面代码注释。
自顶向下归并完整代码:
//归并排序(递归Recursion,自顶向下) public static void sort(int[] arr){ //本方法只会执行一次,下面两个方法执行多次 if(arr == null) return; int[] aux = new int[arr.length]; //辅助数组 sort(arr,aux,0,arr.length-1); } public static void sort(int[] arr,int[] aux,int p,int q){ if(p>=q) return; int mid = (p+q)>>1; sort(arr,aux,p,mid); //左半块归并 sort(arr,aux,mid+1,q); //右半块归并 merge(arr,aux,p,mid,q); //归并详细过程 } public static void merge(int[] arr,int[] aux,int p,int mid,int q){ for(int k=p;k<=q;k++){ //先复制到辅助数组中 aux[k] = arr[k]; } int i=p,j=mid+1; //i、j指向辅助数组左右半块指针,从起始位置开始 for(int k=p;k<=q;k++){ //k指向原数组arr[],根据i、j指针位置判断左右半块是否遍历完 if(i > mid) arr[k] = aux[j++]; //左半块遍历完 else if(j>q) arr[k] = aux[i++]; //右半块遍历完 else if(aux[j]>aux[i]) arr[k] = aux[i++]; else arr[k] = aux[j++]; } }
自底向上归并
上面自顶向下归并是一种基于递归方式的归并,解决大数组排序问题时很好用。实际上我们平时遇到的多数是小数组,所以自底向上归并是先归并那些微小数组,然后再成对归并这些小数组,以此类推,直到将整个数组归并在一起。首先我们进行的是两两归并,然后是四四归并,然后是八八归并,一直进行下去。每趟最后一次归并的第二个子数组长度可能比第一个子数组长度小,其余情况两个子数组长度应该相等,每趟子数组长度翻倍。详细过程见下面代码注释。
自底向上归并完整代码:
//非递归方式 public static void sortNotRecursion(int[] arr){ if(arr == null) return; int[] aux = new int[arr.length]; for(int i=1;i<arr.length;i*=2){ //p-q+1=2*i:即子数组长度为2*i,i为子数组半长,每趟i翻倍 for(int j=0;j<arr.length-i;j+=i*2){ //j:子数组起始位置 int p = j; //子数组头指针 int q = Math.min(j+i*2-1,arr.length-1); //子数组尾指针,取两者最小值仅仅是因为每一趟最后的子数组长度可能小于2*i,最后位置指针j+i*2-1的值可能会超过数组最大索引,此时取最大索引arr.length-1 int mid = j+i-1; //中间位置。注意不能用(p+q)>>1,因为每一趟最后的子数组长度可能小于2*i,q的位置可能是arr.length-1。 merge(arr,aux,p,mid,q); //每一趟最后一个子数组只有长度大于i时才会进行归并操作,小于或等于i则不进行,由j<arr.length-i控制 } } } public static void merge(int[] arr,int[] aux,int p,int mid,int q){ for(int k=p;k<=q;k++){ //先复制到辅助数组中 aux[k] = arr[k]; } int i=p,j=mid+1; //i、j指向辅助数组左右半块指针,从起始位置开始 for(int k=p;k<=q;k++){ //k指向原数组arr[],根据i、j指针位置判断左右半块是否遍历完 if(i > mid) arr[k] = aux[j++]; //左半块遍历完 else if(j>q) arr[k] = aux[i++]; //右半块遍历完 else if(aux[j]>aux[i]) arr[k] = aux[i++]; else arr[k] = aux[j++]; } }
归并排序是一种稳定的排序算法,但它不是原地归并,而是需要一个辅助数组。归并排序的时间复杂度为O(NlogN),空间复杂度为O(N)。
转载请注明出处 http://www.cnblogs.com/Y-oung/p/8964964.html
工作、学习、交流或有任何疑问,请联系邮箱:yy1340128046@163.com