反常积分
- 定积分存在的两个必要条件，积分区间有限，被积函数有界
- 破坏了积分区间的有限性，引出无穷区间上的反常积分
- 破坏了被积函数的有界性，引出无界函数的反常积分
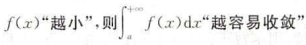
无穷区间上反常积分的概念与敛散性
在反常积分中，一般把∞和使得函数极限为无穷的点（瑕点）统称为奇点
无界函数的反常积分的概念与敛散性
b是f(x)的唯一瑕点，则无界函数f(x)的反常积分定义为
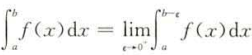若上述极限存在，称反常积分收敛，否则称为发散
- 当x=b为f(x)的无穷间断点，这时f(x)便是一个无界函数了，但积分
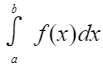可能存在 - 定积分（黎曼积分）存在的必要条件是f(x)有界，但这里的积分是反常积分
- 定积分存在（常义可积），反常积分存在（广义可积）
若a是f(x)的唯一瑕点，则物件函数f(x)的反常积分定义为
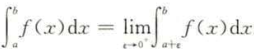若上述极限存在，称反常积分收敛，否则称为发散
若c∈(a, b)是f(x)的唯一瑕点，则无界函数f(x)的反常积分定义为
，若上述右边两个反常积分都收敛，则称反常积分收敛，否则称发散