zoukankan      html  css  js  c++  java

  • 数据结构_6种简单概述_java

    文章目录

    数据结构概述

    数据结构 是数据对象，存在于该对象的实例以及组成实例的数据元素之间的各种关系

“数据对象定义为一个实例或值的集合”

"数据结构是抽象数据类型ADT的物理实现"

    1. 数据结构的内容

    1. 数据的逻辑结构 -----数据元素之间的逻辑关系
    2. 数据的存储结构------ 数据元素及其逻辑关系在计算机存储器中的表示形式
    3. 数据的运算 -----能够对数据进行操作检索、插入、删除、更新、排序
    4. 同一个逻辑结构可以有不同的存储结构
    5. 同一种逻辑结构可以有不同的数据运算集合

    2. 数据结构的分类

    1. 线性结构 -------- 表中各个节点具有线性关系
      1. 是非空集
      2. 有且仅有一个开始节点和一个终端节点
      3. 所有结点最多只有一个直接前趋节点和一个直接后继节点
      4. 栈、队列、串
    2. 非线性结构------- 表中各个节点具有多个对应关系
      1. 是非空集
      2. 一个节点可能有多个直接前趋和直接后继节点
      3. 数组、广义表、树、图

    3. 数据的结构的存储方式

    1. 顺序存储方式 ——— 就是在一块连续的存储区域 一个接着一个地存放数据，（物理位置相邻）
      1. 一般采用数据或者结构数据
    2. 链接存储方式 ——— 逻辑上连接，但是物理位置(不相邻)
      1. 通过引用类型来 表示节点的位置关系
    3. 索引存储——— 采用附加的索引表的方式存储节点信息的一种存储方式，一般形式为 （关键字，地址）
      1. 稠密索引 —— 每个结点在索引表上都有一个索引项，其中索引项的地址指示结点所在的存储位置
      2. 稀疏索引——一组结点在索引表只对应一个索引项，其中索引项的地址指示结点所在的存储位置
    4. 散列存储
      1. 根据结点的关键字直接计算出该节点的存储地址的一种存储方式

    4. 数据类型

    1. 语言自身定义的数据类型 int，char等

    2. ADT（抽象数据类型）

      在这里插入图片描述

      1. 数据抽象，数据封装 两个特征

    5. 常用的数据结构

    1. 数组
    2. 栈
      1. 最大特点就是——先进先出，
    3. 队列
      1. 特点—— 一只容许插入，另一端只容许删除
    4. 链表
    5. 树
    6. 图
    7. 堆
      1. 一般讨论的都是二叉堆，
      2. 特点是—— 根节点的值是所有结点中最小或者最大的，并且根节点的两个子树也是一个堆结构
    8. 散列表

    结构

    顺序表结构

    1. 顺序表就是按照顺序存储方式存储的线性表，该线性表的结点按照逻辑次序一次存放在计算机的一组连续的存储单元中

    2. 顺序表的缺点：

      1. 在插入或者删除 ，往往需要移动大量数据
      2. 如果表比较大，有时很难获取到想当的容量空间

    3. 顺序表的优点：

      1. 容易遍历
      2. 容易查找

    4. 只要知道了该顺序表的首地址及每个数据元素所占用的存储长度，就可以计算出任何一个数据元素的位置

    5. $Loc(ai) = loc(a1) + (i-1)*c $ 1<= i<=n

    6. 简单demo

    7. 结构

      static final int MAXLEN=100; //定义顺序表的最大长度

class DATA{
    String key;		//结点关键字
    String name;
    int age;
}

class SLType{
    DATA[] ListData=new DATA[MAXLEN+1] ; 		//保存顺序表的结构数组
    int listLen;			//顺序表已存结点的数量
}

    链表结构

    1. 链表 是一种动态存储分配的结构形式

    2. 链表的优点：

    3. 容易插入，和删除，不要移动数据，只需要改指针引用

    4. 不存在空间的局限性

    5. 链表的缺点：

      1. 浪费存储空间，每个结点都额外需要一个引用变量，（可以忽略的吧，毕竟优点更大）
      2. 对于链表的访问，只能从头开始，不能像顺序表一样随机访问

    6. 链表结构的分类：

    7. 单链表 —— 每个结点只包含一个引用

    8. 双向链表——每个结点包含两个引用，一个指上，一个下

    9. 单循环链表—— 将终端结点的引用域null 改为指向表头结点或开始结点

    10. 多重链的循环链表——如果将表中结点在多个环上，就构成多重链

    11. CodeDemo

    12. 结构

    class DATA{
    String key;		//结点关键字
    String name;
    int age;
}

class SLType{			// 定义链表结构
    DATA[] nodeData = new DATA();
    CLType nextNode;
}

    栈结构

    1. 首先 堆和栈 是不同的概念，

    2. 栈 是一种线性结构 ，

      1. 顺序栈结构 ——跟顺序表一样的用一组地址的内存单元依次保存栈中的数据
      2. 链式栈结构—— 与链式表一样

    3. 最重要的特点——保存和取出都是一端进行，，后进先出

    4. Demo

    5. 数据结构

      static final int MAXLEN = 50;

class DATA3{
    String name;
    int age;
}
class StackType{
    static final int  MAXLEN =50;
    DATA3[] data = new DATA3[MAXLEN+1];
    int top；//栈顶
}

    队列结构

    1. 队列 也是一种线型结构，

    2. 可以分为

      1. 顺序队列
      2. 链式队列

    3. 队列结构是 特点是—— 一端只能进行删除，一端只能进行插入 ，，先进先出FIFO

    4. demo

    5. 结构

      static final  int QUEUELEN=15;

class DATA4{
    String name;
    int age;
}
class SQType{
    DATA4[] date = new DATA4[QUEUELEN]；	//队列数组
    int head; // 队头
    int tail; // 队尾
}

    树结构

    1. 树 结构 是一种描述 非线性层次关系的数据结构

    2. 树—— n个数据结点的集合，该集合包含一个根结点，下面是互不交叉的子集合，

    3. 基本特征：

      1. 在一个树结构中，有且仅有一个结点没有直接前趋，就是根结点

      2. 除了根结点，其他每个结点尤其仅有一个直接前趋

      3. 每个结点可以任意多个直接后继

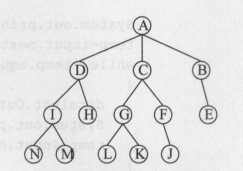
    在这里插入图片描述

    1. 树的一些概念：

      1. 兄弟结点： 具有同一父结点的结点
      2. 结点的度：一个结点所包含子树的数量
      3. 树的度 ： 是指该树 所有结点中最大的度
      4. 叶结点： 树中度为零的结点
      5. 分支结点 ： 树中度不为零的结点
      6. 结点的层数：结点的层数从树根开始计算，根节点为第一层，依次往下
      7. 树的深度： 树中结点的最大层数
      8. 有序树： 若树中各节点的子树是按一定次序从左往右排列的
      9. 无序树：若树中各节点的子树没有按照一定书序排序
      10. 森林 ： n 棵 互不相交的集合

    2. 树 在代码中的表现形式：

      1. 根节点放入一对圆括号中
      2. 根节点的子树从左到右的顺序放入括号中
      3. 对子树做上述相同的处理

      (A(B©),(C(F)),(G(K,L))),(D(H),(I(M,N)))

    1. 二叉树

    1. 区别就是 ：

    2. 每个结点只能有两个子节点，

    3. 左右子树有顺序之分

    4. 二叉树分为

      1. 满二叉树——除最下一层的叶结点外，每层的结点都是两个子节点
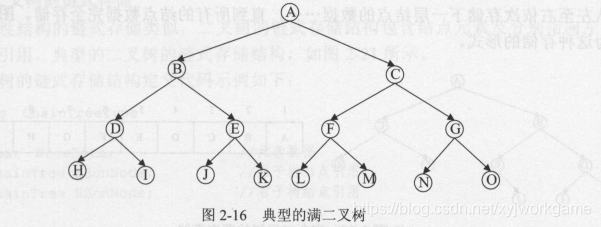
    ![在这里插入图片描述](https://img-blog.csdnimg.cn/20190515122950679.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3h5andvcmtnYW1l,size_16,color_FFFFFF,t_70)

  2. ==完全二叉树==重点—— 在满二叉树的基础上，且 最后一层叶结点按照从左向右的顺序连续存在，

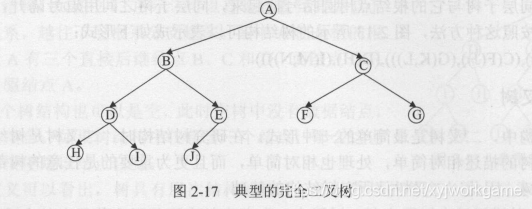
   ![在这里插入图片描述](https://img-blog.csdnimg.cn/20190515122956986.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3h5andvcmtnYW1l,size_16,color_FFFFFF,t_70)

     2.  性质

   ![在这里插入图片描述](https://img-blog.csdnimg.cn/20190515123002619.png)

     3. 存储形式

        1. 一般采用一维数组进行保存

     4. 结构

         1.  顺序结构

             ```java
             static final int MAXLen = 100; //最大结点数
             char[] SeqBinTree = new Char[MAXLen]  //定义数组
             ```

        2.  链式

           ```java
           class ChainTreeType{
               char NodeData;		//元素数据
               ChainTree LSonNode;	// 左子树引用
               ChainTree RSonNode;  //右子树引用
           }
           ```

        3.  有时候可以为了计算方便，添加一个该节点的父节点的引用

         ![在这里插入图片描述](https://img-blog.csdnimg.cn/20190515123010397.png)

           ```java
           class ChainTreeType{
               char NodeData;		//元素数据
               ChainTree LSonNode;	// 左子树引用
               ChainTree RSonNode;  //右子树引用
               Chain ParentNode;  //父节点引用
           }
           ChainTreeType root =null;  //定义根节点引用
           ```

     5. 遍历二叉树 有三种

        1. 先序遍历 ： 即先访问根节点，再按先序遍历左子树，最后按先序遍历右子树。简称DLR

        2. 中序遍历 ： 即先按中序遍历左子树，在访问根节点，最后按中序遍历右子树，LDR

        3. 后续遍历： 即先按后序遍历左子树，再按后续遍历右子树，最后访问根节点，LRD

        4. 按层遍历 ： 从第一层挨个遍历，结点

        5. 四种遍历，在下面代码中
  
       6. [简单demo](https://github.com/xyjworkgame/crazy_java/blob/master/BookNote/src/com/java/algorithm/note/%E6%A0%91%E8%A1%A8.java)

    图结构

    图也是一种非线性结构，例如交通网络等，

    1. 什么是图结构

    1. 每个数据元素之间可以任意关联

    2. 图包含：

      1. 顶点——图中数据元素
      2. 边——连接顶点的线
      3. 一般记为 G=(V,E)G=(V,E) OR G=(V(G),E(G))G = (V(G) , E(G))
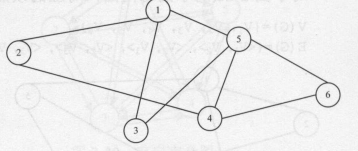
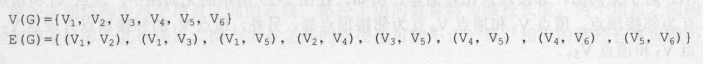
        在这里插入图片描述
        在这里插入图片描述

    3. 图的基本概念

    4. 无向图——边没有方向性

    5. 有向图——边有方向性（在表示的上面，要严格按照顺序来写）

    6. 顶点的度——连接顶点的边的数量

      1. 无向 一般为D(V)D(V)
      2. 有向一般为
        1. 入度——以该顶点为断点的入边数量——ID(V)ID(V)
        2. 出度——以该顶点为断点的出边数量——OD(V)OD(V)

    7. 邻接顶点——指图结构中一条边的两个顶点

      1. 无向图——连接即是邻接
      2. 有向图分为 入边和出边邻接顶点

    8. 无向完全图——每两个顶点之间都存在一条边N个顶点，N(N-1)/2 边数

    9. 有向完全图——每两个顶点之间都存在方向相反的两条边

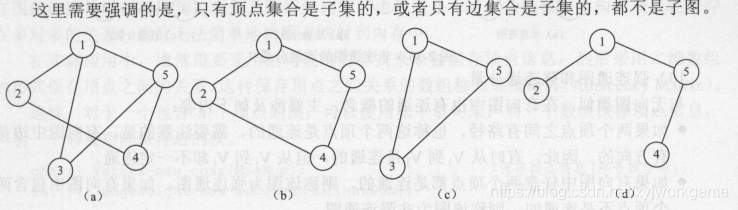
    10. 子图——由于一个完整的图结构包括顶点和边，一个子图的顶点和边都应该是另一个图结构的子集合。
      在这里插入图片描述

    11. 路径——图结构两个顶点之间的连线，路径上边的数量为路径长度

      1. 简单路径——一条零上顶点不重复出现
      2. 环——路劲第一个顶点和最后一个顶点相同
      3. 简单回路——除了第一个和最后一个相同，其他各顶点都不相同

    12. 连通、连通图、连通分量

      1. 两个顶点 之间有路径
      2. 无向图任意两个顶点都是连通的 就是连通图
      3. 无向图的极大连通子图 为连通分量

    13. 强连通、强连通分量

      1. 有有向图 的连通是有方向的
      2. 有向图任意两个顶点都是连通的，为强连通图
      3. 与无向图类似

    14. 权——边中表数的数值

    15. 结构

      char[] Vertex = new Char[MaxNum] ;//保存顶点信息
int[][] EdgeWeight = new int [MaxNum] [MaxNum];//边的权

    16. 简单demo
  • 相关阅读:
    POJ 3660 Cow Contest 任意两点之间的关系 Floyd
    CDOJ 1146 A
    TTTTTTTTTTTTTT CDOJ Sliding Window 线段树（nlogn）或双端队列（n） 模板
    CDOJ 203 并查集+优先队列 好题
    CDOJ 1073 线段树 单点更新+区间查询 水题
    CDOJ 1070 秋实大哥打游戏 带权并查集
    CDOJ 1063 堆排序模板
    CDOJ 1069 秋实大哥去打工 单调栈 下标处理
    CDOJ 1061 C
    巨蟒python全栈开发django14:Form组件
  • 原文地址：https://www.cnblogs.com/YJBlog/p/11054528.html
Copyright © 2011-2022 走看看