0-1 背包问题:给定 n 种物品和一个容量为 C 的背包,物品 i 的重量是 wi,其价值为 vi 。
问:应该如何选择装入背包的物品,使得装入背包中的物品的总价值最大?
分析一波,面对每个物品,我们只有选择拿取或者不拿两种选择,不能选择装入某物品的一部分,也不能装入同一物品多次。
解决办法:声明一个 大小为 m[n][c] 的二维数组,m[ i ][ j ] 表示 在面对第 i 件物品,且背包容量为 j 时所能获得的最大价值 ,那么我们可以很容易分析得出 m[i][j] 的计算方法,
(1). j < w[i] 的情况,这时候背包容量不足以放下第 i 件物品,只能选择不拿 m[ i ][ j ] = m[ i-1 ][ j ]
(2). j>=w[i] 的情况,这时背包容量可以放下第 i 件物品,我们就要考虑拿这件物品是否能获取更大的价值。
如果拿取,m[ i ][ j ]=m[ i-1 ][ j-w[ i ] ] + v[ i ]。 这里的m[ i-1 ][ j-w[ i ] ]指的就是考虑了i-1件物品,背包容量为j-w[i]时的最大价值,也是相当于为第i件物品腾出了w[i]的空间。
如果不拿,m[ i ][ j ] = m[ i-1 ][ j ] , 同(1)
究竟是拿还是不拿,自然是比较这两种情况那种价值最大。
由此可以得到状态转移方程:
if(j>=w[i])
m[i][j]=max(m[i-1][j],m[i-1][j-w[i]]+v[i]);
else
m[i][j]=m[i-1][j];(第一行和第一列为序号,其数值为0)
如m[2][6],在面对第二件物品,背包容量为6时我们可以选择不拿,那么获得价值仅为第一件物品的价值8,如果拿,就要把第一件物品拿出来,放第二件物品,价值10,那我们当然是选择拿。m[2][6]=m[1][0]+10=0+10=10;依次类推,得到m[6][12]就是考虑所有物品,背包容量为C时的最大价值。
#include <iostream>
#include <cstring>
using namespace std;
const int N=15;
int main()
{
int v[N]={0,8,10,6,3,7,2};
int w[N]={0,4,6,2,2,5,1};
int m[N][N];
int n=6,c=12;
memset(m,0,sizeof(m));
for(int i=1;i<=n;i++)
{
for(int j=1;j<=c;j++)
{
if(j>=w[i])
m[i][j]=max(m[i-1][j],m[i-1][j-w[i]]+v[i]);
else
m[i][j]=m[i-1][j];
}
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=c;j++)
{
cout<<m[i][j]<<' ';
}
cout<<endl;
}
return 0;
}
到这一步,可以确定的是可能获得的最大价值,但是我们并不清楚具体选择哪几样物品能获得最大价值。
另起一个 x[ ] 数组,x[i]=0表示不拿,x[i]=1表示拿。
m[n][c]为最优值,如果m[n][c]=m[n-1][c] ,说明有没有第n件物品都一样,则x[n]=0 ; 否则 x[n]=1。当x[n]=0时,由x[n-1][c]继续构造最优解;当x[n]=1时,则由x[n-1][c-w[i]]继续构造最优解。以此类推,可构造出所有的最优解。(这段全抄算法书,实在不知道咋解释啊。。)
``` void traceback() { for (int i = n; i > 1; i--) { if (m[i][c] == m[i - 1][c]) x[i] = 0; else { x[i] = 1; c -= w[i]; } } x[1] = (m[1][c] > 0) ? 1 : 0; } ``` 例:某工厂预计明年有A、B、C、D四个新建项目,每个项目的投资额Wk及其投资后的收益Vk如下表所示,投资总额为30万元,如何选择项目才能使总收益最大? 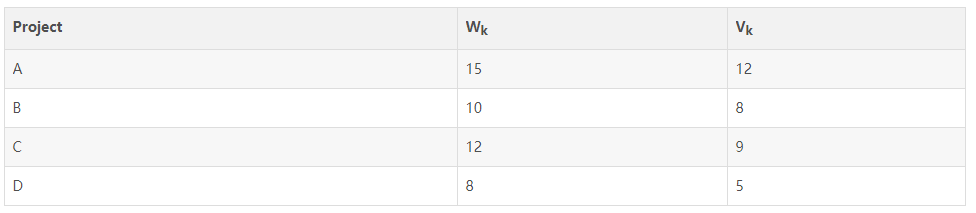
结合前面两段代码
#include <iostream>
#include <cstring>
using namespace std;
const int N=150;
int v[N]={0,12,8,9,5};
int w[N]={0,15,10,12,8};
int x[N];
int m[N][N];
int c=30;
int n=4;
void traceback()
{
for(int i=n;i>1;i--)
{
if(m[i][c]==m[i-1][c])
x[i]=0;
else
{
x[i]=1;
c-=w[i];
}
}
x[1]=(m[1][c]>0)?1:0;
}
int main()
{
memset(m,0,sizeof(m));
for(int i=1;i<=n;i++)
{
for(int j=1;j<=c;j++)
{
if(j>=w[i])
m[i][j]=max(m[i-1][j],m[i-1][j-w[i]]+v[i]);
else
m[i][j]=m[i-1][j];
}
}/*
for(int i=1;i<=6;i++)
{
for(int j=1;j<=c;j++)
{
cout<<m[i][j]<<' ';
}
cout<<endl;
}
*/
traceback();
for(int i=1;i<=n;i++)
cout<<x[i];
return 0;
}
输出x[i]数组:0111,输出m[4][30]:22。
得出结论:选择BCD三个项目总收益最大,为22万元。
不过这种算法只能得到一种最优解,并不能得出所有的最优解。
本文转载自:https://blog.csdn.net/xp731574722/article/details/70766804