目录
0.PTA得分截图

1.本周学习总结
1.1 二叉树结构
1.1.1 二叉树的2种存储结构
- 二叉树的顺序存储结构
由于二叉树的结点至多为 2,因此这种性质使得二叉树可以使用顺序存储结构来描述,在使用顺序存储结构时我们需要令数组的下标体现结点之间的逻辑关系。我们先来看完全二叉树,如果我们按照从上到下,从左到右的顺序遍历完全二叉树时,顺序是这样的:
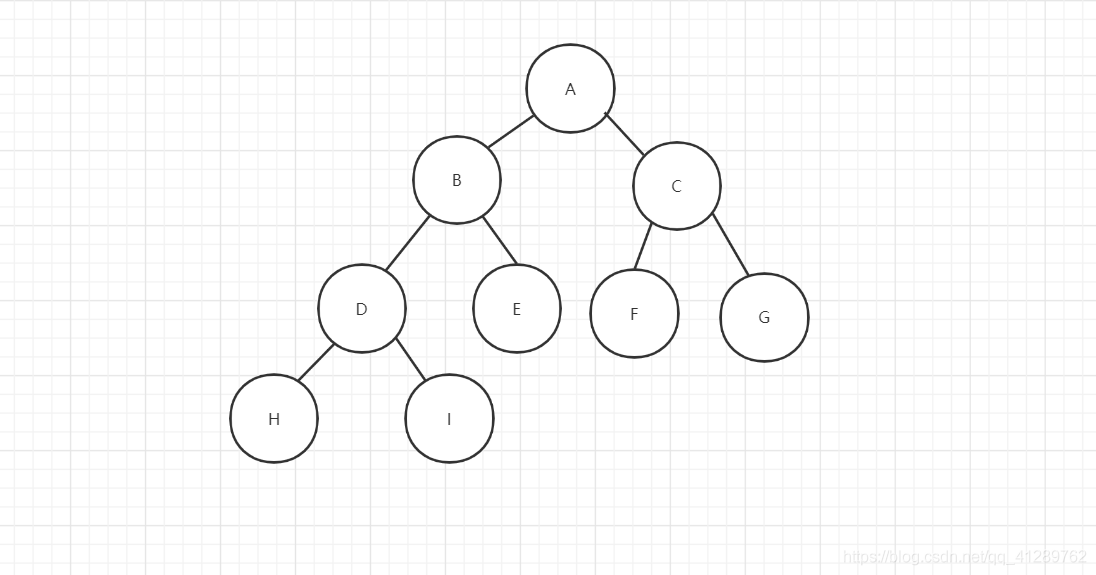
- 二叉树的链式存储结构
结构体相关演示:
typedef struct BiTNode
{
ElemType data; //数据域
ChildPtr *lchild,*rchild; //左右孩子的指针域
//可以开个指针域指向双亲,变为三叉链表
}BiTNode, *BiTree;
1.1.2 二叉树的构造
①顺序存储结构二叉树的建立
Status CreateBiTree(SqBiTree T)
{
int i=0;
printf("请按层序输入结点的值(整型),0表示空结点,输999结束。结点数≤%d:
",MAX_TREE_SIZE);
while(i<10)
{
T[i]=i+1;
if(i!=0&&T[(i+1)/2-1]==Nil&&T[i]!=Nil) /* 此结点(不空)无双亲且不是根 */
{
printf("出现无双亲的非根结点%d
",T[i]);
exit(ERROR);
}
i++;
}
while(i<MAX_TREE_SIZE)
{
T[i]=Nil; /* 将空赋值给T的后面的结点 */
i++;
}
return OK;
}
②链式存储结构二叉树的建立
Status CreateBiTree(SqBiTree T)
{
int i=0;
printf("请按层序输入结点的值(整型),0表示空结点,输999结束。结点数≤%d:
",MAX_TREE_SIZE);
while(i<10)
{
T[i]=i+1;
if(i!=0&&T[(i+1)/2-1]==Nil&&T[i]!=Nil) /* 此结点(不空)无双亲且不是根 */
{
printf("出现无双亲的非根结点%d
",T[i]);
exit(ERROR);
}
i++;
}
while(i<MAX_TREE_SIZE)
{
T[i]=Nil; /* 将空赋值给T的后面的结点 */
i++;
}
return OK;
}
1.1.3 二叉树的遍历
1.二叉树的先序遍历
void PreOrderTraverse(BiTree T)
{
if(T == NULL)
return ;
printf("%c",T->data);/*显示结点数据*/
PreOrderTraverse(T->lchild);/*先序遍历左子树*/
PreOrderTraverse(T->lchild);/*先序遍历右子树*/
}
2.二叉树的中序遍历
void PreOrderTraverse(BiTree T)
{
if(T == NULL)
return ;
printf("%c",T->data);/*显示结点数据*/
PreOrderTraverse(T->lchild);/*先序遍历左子树*/
PreOrderTraverse(T->lchild);/*先序遍历右子树*/
}
3.二叉树的后序遍历
void PreOrderTraverse(BiTree T)
{
if(T == NULL)
return ;
printf("%c",T->data);/*显示结点数据*/
PreOrderTraverse(T->lchild);/*先序遍历左子树*/
PreOrderTraverse(T->lchild);/*先序遍历右子树*/
}
4.二叉树的层序遍历
层序遍历法就是从第一层(根结点)开始,按照从上到下,从左到右的顺序进行遍历,如图所示。

1.1.4 线索二叉树
按照某种遍历方式对二叉树进行遍历,可以把二叉树中所有结点排序为一个线性序列。在该序列中,除第一个结点外每个结点有且仅有一个直接前驱结点;除最后一个结点外每一个结点有且仅有一个直接后继结点。这些指向直接前驱结点和指向直接后续结点的指针被称为线索(Thread),加了线索的二叉树称为线索二叉树。
1.1.5 二叉树的应用--表达式树
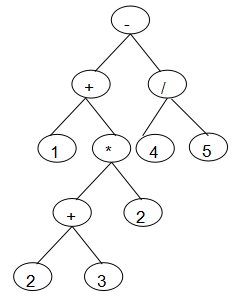
- 代码实现:
void InitExpTree(BTree &T,string str)
{
stack<BTree> s;
stack<char> op;
op.push('#');
int i=0;
while(str[i])
{
if(!In(str[i]))
{
T = new BTNode;
T->data = str[i++];
T->lchild = T->rchild = NULL;
s.push(T);
}
else
{
switch(Precede(op.top(),str[i]))
{
case '<':
op.push(str[i]);
i++;
break;
case '=':
op.pop();
i++;
break;
case '>':
T = new BTNode;
T->data = op.top();
T->rchild = s.top();
s.pop();
T->lchild = s.top();
s.pop();
s.push(T);
op.pop();
break;
}
}
}
while(op.top()!='#')
{
T=new BTNode;
T->data = op.top();
T->rchild = s.top();
s.pop();
if(!s.empty())
{
T->lchild = s.top();
s.pop();
}
s.push(T);
op.pop();
}
T = s.top();
}
double EvaluateExTree(BTree T)
{
double sum=0,a,b;
if(!T->lchild && !T->rchild)
{
return T->data-'0';
}
b = EvaluateExTree(T->rchild);
a = EvaluateExTree(T->lchild);
//b = EvaluateExTree(T->rchild);
switch(T->data)
{
case '+':
return a+b;
break;
case '-':
return a-b;
break;
case '*':
return a*b;
break;
case '/':
if(b==0)
{
cout << "divide 0 error!" << endl;
exit(0);
}
return a/b;
break;
}
}
1.2 多叉树结构
1.2.1 多叉树结构
- 孩子兄弟表示法
从双亲的角度和从孩子的角度研究树的存储结构,如果我们从树节点的兄弟的角度去考虑会怎么样呢?当然,对于树这样的层级结构来说,只研究几点的兄弟是不行的,我们观察后发现,任意一棵树,它的结点的第一个孩子如果存在就是唯一的,它的右兄弟如果存在也是唯一的。因此,我们设置两个指针,分别指向该结点的第一个孩子和此结点的右兄弟。
结点结构如下表示:
typedef struct CSNode
{
ElemType data; //数据域
struct CSNode *firstchild; //指向对应长子结点的指针域
struct CSNode *rightsib; //指向对应右兄弟结点的指针域
}CSNode,*CSTree;
1.2.2 多叉树遍历
1.3 哈夫曼树
1.3.1哈夫曼树的定义
- 给定n个权值作为n个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。
- 哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
- WPL计算方法:
WPL=求和(wi li)其中wi是第i个节点的权值(value)。li是第i个节点的长(深)度.
1.3.2 哈夫曼树的结构体
typedef struct
{ char data; //节点值
float weight; //权重
int parent; //双亲节点
int lchild; //左孩子节点
int rchild; //右孩子节点
} HTNode;
1.3.3 哈夫曼树构建及哈夫曼编码
- 构造哈夫曼树
1.概念:哈夫曼树为带权路径最短的二叉树
2.构造过程:每次选出最小的两个顶点,分别作为左右分支,构造出父节点,父节点权值为两顶点之和,然后将其加入到顶点集合中,并删除之前取出的两个顶点。 - 哈夫曼编码
1.算法思想:通过递归,从根结点往每个叶子结点来进行编码。通过一个临时数组来按照左零右一存储下来,若遇到叶子结点,则将存储的路径作为该字符的编码。
void CreateHuffmanTree(BinaryTree &T, ElemType a[],int n)
{
TNode **Data = new TNode *[n];
for (int i = 0; i < n; i++)
{
TNode *p = new TNode;
p->data = a[i];
p->lchild = NULL;
p->rchild = NULL;
Data[i] = p;
}
for (int i = 0; i < n - 1; i++) //n个结点 需要n-1次循环
{
//每次取两个最小的结点构造哈夫曼树
TNode *p = new TNode;
p->data = Data[0]->data + Data[1]->data;
p->lchild = Data[0];
p->rchild = Data[1];
//删除两个最小结点
for (int i = 2; i < n; i++)
Data[i - 2] = Data[i];
//增加新建的结点
int j = n - i - 2; //j指向未加入哈夫曼树的最大顶点
if (j != 0) //j不等于0 用直接插入排序 插入新建的顶点
{
if (p->data < Data[j]->data)
{
for (j; j >= 0 && p->data < Data[j]->data; j--)
Data[j + 1] = Data[j];
Data[j + 1] = p;
}
else
Data[j] = p;
}
else //j等于0 说明为哈夫曼树的根结点 直接赋值
Data[j] = p;
}
//最后数组里只有一个结点 则哈夫曼树构造完成
T = Data[0];
delete []Data; //释放辅助数组空间
}
void CreateHuffmanCode(BinaryTree T,char *Code[], int n)
{
static int i = 0; //i为编码字符的编号
static int j = 0; //j为每个字符应编码的长度 初试话为0
static char *c = new char[n];
if (T)
{
if (!T->lchild && !T->rchild) //如果为叶子结点 则按照左0右1规则编码
{
c[j++] = '�'; //结束符
Code[i] = new char[j]; //分配j的长度
strcpy(Code[i++],c); //串复制
j--; //取消结束符
}
if (T->lchild) //左0
{
c[j++] = '0';
CreateHuffmanCode(T->lchild,Code,n);
j--;
}
if(T->rchild) //右1
{
c[j++] = '1';
CreateHuffmanCode(T->rchild,Code,n);
j--;
}
}
delete []c;
}
1.4 并查集
- 并查集的结构体
typedef struct node
{ int data; //结点对应人的编号
int rank; //结点秩:子树的高度,合并用
int parent; //结点对应双亲下标
} UFSTree; //并查集树的结点类型
- 初始化并查集
void MAKE_SET(UFSTree t[],int n) //初始化并查集树
{ int i;
for (i=1;i<=n;i++)
{ t[i].data=i; //数据为该人的编号
t[i].rank=0; //秩初始化为0
t[i].parent=i; //双亲初始化指向自已
}
}
- 并查集的查找
int FIND_SET(UFSTree t[],int x) //在x所在子树中查找集合编号
{ if (x!=t[x].parent) //双亲不是自已
return(FIND_SET(t,t[x].parent)); //递归在双亲中找x
else
return(x); //双亲是自已,返回x
}
- 并查集的合并
void UNION(UFSTree t[],int x,int y) //将x和y所在的子树合并
{ x=FIND_SET(t,x); //查找x所在分离集合树的编号
y=FIND_SET(t,y); //查找y所在分离集合树的编号
if (t[x].rank>t[y].rank) //y结点的秩小于x结点的秩
t[y].parent=x; //将y连到x结点上,x作为y的双亲结点
else //y结点的秩大于等于x结点的秩
{ t[x].parent=y; //将x连到y结点上,y作为x的双亲结点
if (t[x].rank==t[y].rank) //x和y结点的秩相同
t[y].rank++; //y结点的秩增1
}
}
1.5.谈谈你对树的认识及学习体会
1.树形结构的应用非常广泛,判定树和哈夫曼树可分别用于求解分类问题和有效分类问题以及哈夫曼编码,哈夫曼编码算法的关键点是:每次合并具有最小权值和次小权值的两个根结点,直到只剩下一个根结点为止。 对哈夫曼树的每个结点的左分支和右分支分别置“0”或“1”,就可得到哈夫曼编码。
2.PTA实验作业
2.1二叉表达式树
2.1.1 解题思路及伪代码
1.解题思路:
2.伪代码:
void InitExpTree(BTree& T, string str)
{
定义符号栈,数字栈;
定义 len=str.size();
for i = 0 to len
ch = str.at(i);
if ch是符号
判断符号与栈顶符号优先级;
if < T入栈,op栈顶出栈;
if > ch入栈;
if = 栈顶出栈;
end if;
if ch是数字
入栈;
end if;
end for;
逐个出栈;
}
double EvaluateExTree(BTree T)
{
定义 left,right;
if T为叶子结点
return T;
left = EvaluateExTree(T->lchild);
right = EvaluateExTree(T->rchild);
switch (ch)
answer = left ch right;
return answer;//得到最终计算结果
}