二叉树链式存储结构
二叉树每个结点最多有两个孩子,所以设计一个数据域两个指针域。称这样的链表叫做二叉链表。

其中data是数据域,lchild和rchild都是指针域,分别存放指向左孩子和右孩子的结点。
二叉链表的结点结构定义代码:
struct BiTNode { char ch; //结点数据 struct BiTNode *lchild; //左孩子指针 struct BiTNode *rchild; //右孩子指针 };
 结构示意如图:
结构示意如图:
遍历二叉树
二叉树的遍历是指从根结点出发,按照某种次序依次访问二叉树中所有结点,使得每个结点被访问一次且仅被访问一次。
1.前序遍历
二叉树为空,则空操作返回,否则先访问根结点,然后前序遍历左子树,再前序遍历右子树。 根 左 右
 先根A
先根A
BDGH左树 --> 再根B --> DGH一颗树 --> 再根D --> 再G --> H
CEIF右树 --> 再根C --> EI一颗树 --> 再根E 左没有,右--> I --> F
ABDGHCEIF
2.中序遍历
二叉树为空,则空操作返回,否则中序遍历根结点的左子树,然后访问根结点,最后中序遍历右子树。 左 根 右
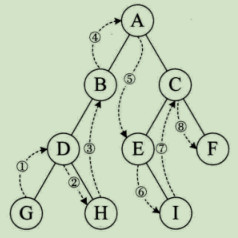 先左数BDGH 再A 最后右树 CEIF
先左数BDGH 再A 最后右树 CEIF
先左树B下面又是一颗树再左树D下面又是一颗树再左树G 下面没有左树了就返回根 G 右树没有 返回根D 右树H 左右子树没有 返回根B 右树没有返回根A 右树开始 先左树CEI 下面又是一颗树再左树E 左树没有返回根E 右树I没有左右树返回根C 右树F开始 没有左子树返回根F。
最终 GDHBAEICF
3.后序遍历
二叉树为空,则空操作返回,否则从左到右先叶子后结点的方式遍历访问左右子树,最后访问根结点。 左 右 根
 GHDBIEFCA
GHDBIEFCA
二叉树前序遍历递归算法:
void Recursion(struct BiTNode *root) { if (NULL == root)
return; printf("%c ", root->ch); Recursion(root->lchild); //遍历左子树 Recursion(root->rchild); //遍历右子树 }
二叉树中序遍历递归算法:
void Recursion(struct BiTNode *root) { if (NULL == root) return;
Recursion(root->lchild); //遍历左子树 printf("%c ", root->ch); Recursion(root->rchild); //遍历右子树 }
二叉树后序递归遍历算法:
void Recursion(struct BiTNode *root) { if (NULL == root) return; Recursion(root->lchild); //遍历左子树 Recursion(root->rchild); //遍历右子树 printf("%c ", root->ch); }
#define _CRT_SECURE_NO_WARNINGS #include<stdio.h> #include<stdlib.h> struct BiTNode { char ch; //结点数据 struct BiTNode *lchild; //左孩子指针 struct BiTNode *rchild; //右孩子指针 }; void Recursion(struct BiTNode *root) { if (NULL == root) return; Recursion(root->lchild); //遍历左子树 Recursion(root->rchild); //遍历右子树 printf("%c ", root->ch); } void test() { struct BiTNode nodeA = { 'A',NULL,NULL }; struct BiTNode nodeB = { 'B',NULL,NULL }; struct BiTNode nodeC = { 'C',NULL,NULL }; struct BiTNode nodeD = { 'D',NULL,NULL }; struct BiTNode nodeE = { 'E',NULL,NULL }; struct BiTNode nodeF = { 'F',NULL,NULL }; struct BiTNode nodeG = { 'G',NULL,NULL }; struct BiTNode nodeH = { 'H',NULL,NULL }; struct BiTNode nodeI = { 'I',NULL,NULL }; nodeA.lchild = &nodeB; nodeA.rchild = &nodeC; nodeB.lchild = &nodeD; nodeD.lchild = &nodeG; nodeD.rchild = &nodeH; nodeC.lchild = &nodeE; nodeC.rchild = &nodeF; nodeE.rchild = &nodeI; Recursion(&nodeA); } int main() { test(); system("pause"); }
推导遍历结果
已知一颗二叉树的前序遍历序列为 ABCDEF,中序遍历序列为 CBAEDF,请问这颗二叉树后序遍历结果是多少?
前序遍历先打印根再递归左右子树。所以前序遍历序列为ABCDEF,第一个字母是A被打印出来,就说明A是根结点的数据。中序遍历先递归左子树再打印根再递归右子树。中序遍历CBAEDF,可以知道C、B是A的左子树结点,E、D、F是A的右子树结点。
然后看前序中C和B,它的顺序是ABCDEF,是先打印B后打印C,所以B应该是A的左孩子,而C就只能是B的孩子,此时是左还是右孩子不确定。再看中序CBAEDF,C是在B的前面打印,这就说明C是B的左孩子,否则就是右孩子(右孩子中序就是先打印B)。
再看前序中的E、D、F,它的顺序是ABCDEF,那就意味着D是A结点的右孩子,E和F是D的子孙,注意,它们中有一个不一定是孩子,还有可能是孙子。再看中序序列CBAEDF,由于E在D的左侧,而F在右侧,所以可以确定E是D的做孩子,F是D的右孩子。因此最终得到二叉图:
 由图可知后序遍历结果: CBEFEA
由图可知后序遍历结果: CBEFEA
例二:已知一颗二叉树中序序列是ABCDEFG,后序序列式BDCAFGE,求前序序列。
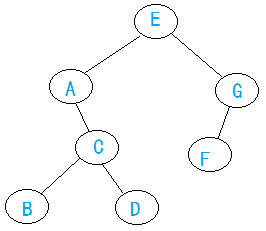 推理出结构图可知前序序列为:EACBDGF
推理出结构图可知前序序列为:EACBDGF
从这里得出两个二叉树遍历的性质:
已知前序遍历序列和中序遍历序列,可以唯一确定一颗二叉树
已知中序遍历序列和后序遍历序列,可以唯一确定一颗二叉树
注意:已知前序和后序,是不确定一颗二叉树的。原因也很简单,比如前序序列ABC,后序序列CBA。我们可以确定A一定是根结点,但接下来无法知道那个结点是左子树,那个是右子树。这棵树可能如图所示:

二叉树建立
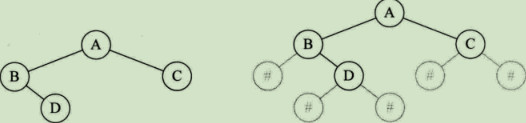
将二叉树中每个节点的空指针引出一个虚结点,其值为一特定值,比如“#”。我们称这种处理后的二叉树为原二叉树的扩展二叉树。假设二叉树的结点均为一个字符,把刚才前序遍历序列如AB#D##C##用键盘挨个输入。实现算法如下:
#define _CRT_SECURE_NO_WARNINGS #include<stdio.h> #include<stdlib.h> typedef struct Node //二叉树链表结点结构定义 { char data; //结点数据 struct Node *lchild; //左孩子指针 struct Node *rchild; //右孩子指针 }BiTNode,*BiTree; //按前序输入二叉树中结点的值(一个字符) //#表示空树 void CreateBiTree(BiTree *T) { //为什么这里是struct ** (BiTree *)二级指针???????????? char ch; scanf("%c", &ch); if (ch == '#') *T = NULL; else { *T = ( BiTNode *)malloc(sizeof(BiTNode)); if (!*T) exit(-1);
(*T)->data = ch; //生成根结点 CreateBiTree(& (*T)->lchild); //构建左子树 CreateBiTree(& (*T)->rchild); //构建右子树 } } void Recursion(BiTNode *root) //前序遍历 { if (NULL == root) return; printf("%c ", root->data); Recursion(root->lchild); //遍历左子树 Recursion(root->rchild); //遍历右子树 } int main() { BiTree T = NULL; CreateBiTree(&T); Recursion(T); //前序遍历打印结点出来 system("pause"); }
当然,完全可以用中序或后序遍历的方式实现二叉树的建立,只不过代码里生成结点和构造左右子树代码顺序交换一下。
另外,输入的字符也要做相应的更改。如上图扩展二叉树的中序遍历字符串应该为#B#D#A#C#,而后序字符串应该为###DB##CA。