机器学习算法可以通过学习就可以弄清楚如何去执行一些重要的任务。在手动编程不可行的情况下,这种方法通常既可行又经济有效。随着可获取的数据在逐步增多,越来越多更加复杂的问题可以用机器学习来解决。事实上,机器学习已经被广泛的运用到计算机以及一些其他领域。然而,开发出成功的机器学习应用需要大量的“black art”,这些内容是很难在教科书中找到的。
我最近读了华盛顿大学的Pedro Domingos教授的一篇十分惊艳的技术论文,题是“A Few Useful Things to Know about Machine Learning”。 它总结了机器学习研究人员和实践者所学到的12个关键的经验及教训,包括要避免的陷阱,需要关注的重点问题以及常见问题的答案。我想在本文中分享这些十分宝贵的经验教训,因为当你思考解决下一个机器学习问题时,这些经验会对你十分有用。
1.学习 = 表示 + 评估 + 优化
所有的机器学习算法通常由3个部分组成:
- 表示:分类器必须用计算机能处理的某种形式语言来表示。 反过来讲,为学习器选择一种表示就等于选择它可能学习的一组分类器集合。这个集合被称为学习器的假设空间。如果某个分类器不在假设空间中,那么就不能被学习到。与此相关的一个问题是如何表示输入,也就是说要用哪些特征,本文稍后介绍。
- 评估:需要一个评估函数来区分好的分类器和坏的分类器。机器学习算法内部使用的评估函数可能与我们希望分类器优化的外部评估函数有所不同,为了更好的优化,接下来会进一步讨论。
- 优化:最后,我们需要一种方法可以在假设空间中找到评价函数得分最高的那个分类器。优化技术的选择对于学习器的效率至关重要,并且当评估函数有多个最优值时,优化技术也有助于确定所产生的分类器。 初学者开始使用现成的优化器是很常见的,之后这些方法会被定制设计的优化器所取代。
 机器学习算法组成
机器学习算法组成
2.泛化才是关键
机器学习的最终目的是将训练模型应用在除训练样本之外的其他数据中。因为无论我们训练时有多少数据,在测试的时候我们都不太可能再次遇到与这些训练时的详细数据完全相同的情况。在训练集上获得好的结果很容易。机器学习初学者中最常见的错误就是对训练数据进行测试并自以为大获成功。如果选择的分类器在全新的数据上进行测试,它们通常表现的还不如随机猜测所得的结果好。所以,如果你要雇佣某人来构建分类器,一定要保留一些数据给你自己,之后再用这些数据来测试他们给你的分类器。反过来讲,如果你被雇来构建分类器,从一开始就划分出一些数据用作之后的测试,在你用全部数据进行训练并得到您的分类器过后,再用这部分数据来测试你最终选择的分类器。
3.只有数据是不够的
将泛化作为目标还有另一个主要的问题:只有数据是不够的,不管你有多少数据。
这似乎是个相当令人沮丧的消息。那么我们还怎么希望学到所有东西呢?幸运的是,在现实世界中我们想学习的函数并不是均匀的来自所有可能函数的!事实上,许多通用的假设往往会起很大的作用 ——像平滑性、相似的示例有相似的分类、有限的相关性、或有限的复杂性等,这也是机器学习会取得成功的很大一部分原因。与演绎法一样,归纳法是一种知识杠杆:将少量的知识输入转化成大量的知识输出。归纳是一个比演绎更强大的杠杆,需要更少的知识输入来获取有用的结果,但是,它终究还是不能在没有知识输入的情况下工作。而且,正如杠杆一样,我们投入的越多,我们可以获取的知识就越多。
 数据资源
数据资源
综上来看,机器学习需要知识这点并不奇怪。机器学习不是魔术, 它并不能做到从无到有。它可以做到的是从少变多。像所有的工程技术一样,编程有很多工作要做:我们必须从抓取开始构建所有的东西。机器学习更像是种田,让大自然完成大部分的工作。农民将种子与营养物质结合起来种植庄稼。而机器学习则是将知识与数据结合起来,来构建模型。
4.过拟合有多张面孔
如果我们的知识和数据不足以完全学习出正确的分类器怎么办?那么我们就冒着得到一个幻想中的分类器的风险来构建,这些分类器可能与实际情况相差甚远,它简单的将数据中的巧合当做了一般情况。这个问题被称为“过拟合”,是机器学习中的难题。当你的学习器输出的分类器在训练数据上有100%的准确率,但在测试数据上只有50%的准确率的时候,这就是过拟合。在正常情况下,无论在训练集还是在测试集它的准确率都应该为75%。
在机器学习中,每个人都知道过拟合,但它有很多形式,有些并不会马上显现出来。理解过拟合的一种方法是将泛化误差分解为偏差和方差。偏差是学习器有不断学习同样错误的倾向。方差是学习器倾向于去学习随机事物,不考虑真实信号是如何。线性学习器有很高的偏差,因为当两个类的交界不是一个超平面时,线性学习器就无法进行归纳。决策树就不存在这个问题,因为它们可以表示任意布尔函数,但在另一方面,决策树有较大的方差:决策树在同一现象产生的不同训练集上学习,所便显出的结果是完全不同的,但理论上它们的结果应该是相同的。
 机器学习多面性
机器学习多面性
交叉验证有助于减弱过拟合,例如通过使用交叉验证来选择决策树的最佳尺寸来学习。但这不是万能的,因为如果我们使用了过多的参数,那模型本身就已经开始过拟合了。
除了交叉验证之外,还有很多方法可以预防过拟合的问题。最常用的方法就是给评估函数添加一个正则项。这样做可以惩罚许多较为复杂的模型,从而有利于产生较为简单的模型。另一种方法是在添加新的结构之前,通过像卡方检验来测试统计显著性,以确定加入这种结构是否会有帮助。当数据十分稀少时,这些技术特别有用。尽管如此,你还是应该对存在某种技术可以“解决”过拟合问题这样的说法持怀疑态度,这十分容易就会让过拟合变为欠拟合。想要同时避免这两种情况需训练出一个完美的分类器,根据天下没有免费的午餐原理,如果事先并没有足够的知识,不会有任何一种单一技术可以一直表现最好。
5.高维度下直觉失效
在过拟合之后,机器学习中最大的问题就是维度灾难。 这个表达式是由Bellman在1961年提出的,指出了一个事实:当输入是高维度时,许多在低维度上工作正常的算法效果变得很差。 但是在机器学习领域,维度灾难这个词还有更多的含义。随着示例数据的维数(特征数量)的升高,正确地泛化的难度在以指数增加,因为固定大小的训练集只覆盖了输入空间的一小部分。
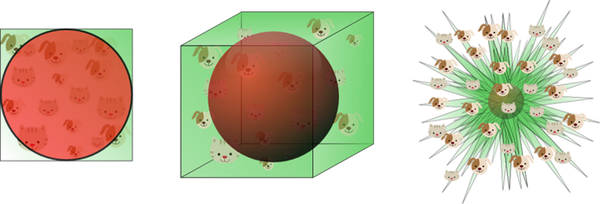 高维空间
高维空间
高维空间中比较普遍的问题是我们直觉失效,我们来自三维世界的直觉通常不适用于高维空间。在高维空间中,多元高斯分布的大部分质量并不接近平均值,而是在逐渐远离均值的一层“壳”上;打个比方,一个高维度的橙子的大部分质量都在皮上,而不在瓤里。如果恒定数量的示例在高维超立方体中均匀分布,那么超出某个维度后,大多数示例将更接近于超立方体的一个面。如果我们在超立方体内内接一个超球面,那么在高维度下,超立方体的几乎所有质量都将分布在超球面之外。这对于机器学习来说是个坏消息,因为机器学习经常用一种类型的形状来近似另一种类型的形状。
在二维或三维空间内建立分类器是很容易的;我们可以通过肉眼观察找出不同类别的示例之间合理的分界线。但是在高维度空间中我们很难理解正在发生什么。反过来说这让设计一个好的分类器变得很难。人们可能会天真的认为收集更多的特征并不会有什么害处,因为在最坏的情况下,它们也只不过不提供关于类别的新信息而已,但在实际情况下,这样做的好处可能远小于维度灾难所带来的问题。
6.理论担保与实际看上去并不一样
机器学习论文中充满了理论的担保。最常见的类型是可以确保良好泛化所需要的示例数据的界限。你应该如何理解这些担保呢?首先,需要注意它们是否可行。归纳传统上与演绎是相反的:在演绎中你可以保证结论是正确的;在归纳中这些都不好说。或者说这是许多世纪以来留下的传统观点。近几十年来的一个显著的提升是,我们认识到在实际情况中我们可以对归纳的结果的正确性有所保证,特别是如果我们愿意接受概率担保。
我们必须小心边界所包含的意义。例如,边界并不意味着,如果你的学习器返回了一个与特定训练集上相一致的假设,那么这个假设可能泛化的很好。边界的意思是,给定一个足够大的训练集,很有可能你的学习器要么可以返回一个泛化良好的假设,要么无法找到一个保持正确的假设。这个边界也无法告诉我们如何去选择一个好的假设空间。它只告诉我们,如果假设空间包含了真实的分类器,那么学习器输出一个不好的分类器的概率会随着训练数据的增加而减少。如果我们缩小假设空间,边界就会有所改善,但是假设空间包含真实分类器的几率也会降低。
 理论与实际
理论与实际
另一种常用的理论担保是渐近:给定无限的数据,可以保证学习器输出正确的分类器。这个保证让人欣慰,但仅仅因为渐进的保证而确定一个学习器是十分草率的。在实践中,我们很少处于渐近状态。而且,由于上文讨论的偏差 - 方差的权衡,在无限数据下,如果学习器A比学习器B表现好,则在有限数据中,学习器B往往比学习器A表现的要好。
机器学习中理论保证的主要作用不是作为实践中决策的标准,而是在算法设计中作为理解和驱动的来源。在这方面,他们是相当有用的;事实上,理论与实践的密切配合是机器学习多年来取得如此巨大进步的主要原因之一。但要注意:学习是一个复杂的现象,因为学习器既有理论证实,并且可实际应用,但这并不意味着前者是后者的依据。
7.特征工程是关键
在一天结束时,总有一些机器学习项目会成功,而一些会失败。是什么造成了它们之间的差异?显然最重要的影响因素是特征的使用。如果你有许多独立的特征, 这些特征类别都有很好的关联,那么学习起来就很容易。另一方面,如果这个类别与特征的关系十分复杂,那么你可能就无法学习它。通常情况下,原始数据不可直接用来学习,但是可以从中构建特征。这通常是机器学习项目中主要工作所在。它往往也是机器学习中最有趣的一部分,直觉,创造力和“black art”与技术一样重要。
初学者常常惊讶于机器学习项目中真正用于学习的时间太少。但是,如果你考虑了在数据收集,整合,清理和预处理上所花费的时间,以及在特征设计中进行的无数次试验与失败,这些就都说得通了。另外,机器学习不是建立数据集和运行学习器的一个一次性过程,而是一个运行学习器,分析结果,修改数据和/或学习器等不断重复,反复迭代过程。真正的学习通常是这些内容中最快的一部分,这是因为我们已经非常精通它了!特征工程更加困难,因为它是一个特定领域的,而学习器在很大程度上是通用的。但是,这两者之间没有明确的界限,这也是最有用的学习器往往是那些可以促进知识整合的学习器的另一个原因。
 特征工程
特征工程
8.更多的数据胜过更聪明的算法
在大多数计算机科学中,有两种主要资源是有限的:时间和内存。在机器学习中,还有第三种:训练数据。其中哪一个资源会成为瓶颈是随着时间而改变的。在八十年代,瓶颈往往是数据。当今通常是时间。现在大量的可用数据,但并没有足够的时间来处理它们,所以这些数据常常被弃用。这就造成了一个悖论:即使原则上更多的数据意味着我们可以学习更复杂的分类器,而实际上我们通常会使用简单的分类器,因为复杂的分类器需要很长的时间去学习。
使用更聪明的算法取得的回报要比你预期的更少,一部分原因是,机器学习的工作机制都十分的相似。这个结论也许令你十分吃惊,特别是当你考虑到规则集和神经网络的表示方法差异是很明显时。但事实上,命题规则可以很容易被编码为神经网络,并且其他表示之间也存在类似的关系。所有学习器本质上都是通过将附近的示例分到同一类内来工作;关键的区别在于对“附近”的定义。对于非均匀分布的数据,不同的学习器可以产生广泛不同的边界,同时在重要领域(即具有大量训练示例,并且测试示例也有很大概率出现的领域)仍能做出相同的预测。这也有助于解释为什么强大的学习器虽然不稳定,但仍然准确。
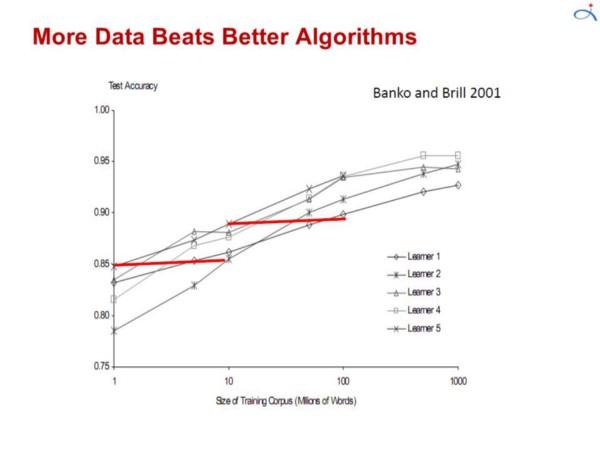 数据胜于算法
数据胜于算法
通常,首先尝试最简单的学习器是值得的(例如,在逻辑回归之前先尝试朴素贝叶斯,在支持向量机之前先尝试近邻)。更复杂的学习器固然诱人,但他们通常来说更难使用,因为它们需要调节更多的参数才能获得好的结果,并且他们的内部机制更不透明)。
学习器可以分为两大类:一类的表示具有固定大小的,比如线性分类器,另一类的表示可以随着数据一起增长,如决策树。固定大小的学习器只能利用有限的数据。原则上可变大小的学习器可以利用给定的充足数据学习任何函数,但实际上由于算法和计算成本的限制,这些通常是无法做到的。而且,由于维度灾难,不存在会被认为充足的数据量。正是因为这些原因,只要你愿意付出努力,聪明的算法(那些充分利用数据和计算资源的算法)往往最终会得到回报。设计学习器和学习分类器之间没有明确的界限;相反,任何给定的知识都可以在学习器中编码或从数据中学习。所以机器学习项目往往会有学习器设计这一重要组成部分,机器学习实践者需要在这方面具备一定的专业知识。
9.要学习许多模型,不仅仅是一个
在机器学习的早期,每个人都有自己喜欢的学习器,并有一些先入为主的观念坚信它的优越性。人们付出大量的努力去尝试它的多种变化,并选择其中最好的一个。之后,通过系统的实践比较表明,最好的学习器是随着应用的改变而有所不同的,因此包含许多不同学习器的系统开始出现。现在,努力尝试许多学习器的不同变化,仍然是为了选择最好的那一个。但随后研究人员注意到,如果不是只选最好的那一个,而是将多种情况进行结合,结果会更好——通常要好得多——而且对用户来说几乎不需花费额外的努力。
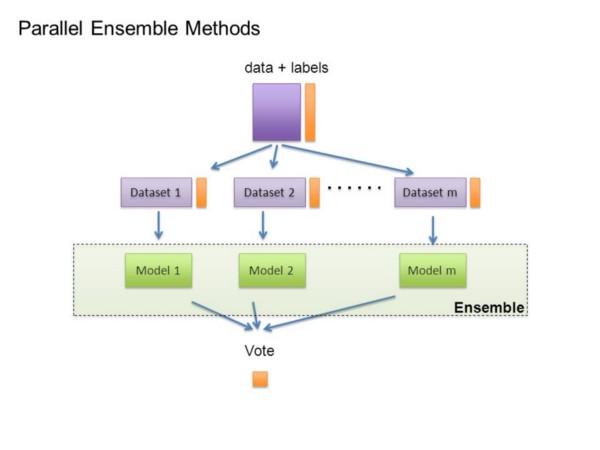 平行集成方法
平行集成方法
现在创建这样的模型集成已经实现标准化。最简单的集成技术称为bagging,我们通过重采样简单地随机生成不同的训练集,每个集合上分别学习一个分类器,并通过投票的方式将结果进行合并。这是有效的,因为它大大降低了方差,而只是稍微增加了偏差。在boosting方法中,每个训练样本都有权重,而且这些都是不同的,以至于每个新的分类器都集中在前面那些往往会出错的例子上。在stacking方法中,单个分类器的输出会成为“高级”学习器的输入,这个学习器可以计算出如何最好地组合这些来自“低层”的输出。
还存在许多其他技术,现在的趋势是越来越大的集成。在Netflix大奖中,来自世界各地的团队争相构建最佳视频推荐系统。随着比赛的进行,团队们发现通过将他们的学习器与其他团队的学习器进行合并,会取得了最好的结果,并且可以合并为越来越大的团队。冠军和亚军都合并超过了100个学习器,并且这两者集成后又进一步提升了效果。毫无疑问,我们将来会看到更大的集成学习器。
10.简单并不意味着准确
著名的奥卡姆剃刀原理称,如果没有必要就不要增加实体。在机器学习中,这通常意味着,给定两个具有相同训练误差的分类器,两者中较简单的那个可能具有最低的测试误差。有关这一说法的证明在文献中经常出现,但实际上有很多反例,并且“没有免费的午餐”定理也暗示它不可能是真实的。

我们在前一节已经看到一个反例:模型集成。集成模型的泛化误差会随着添加分类器而不断的改进。因此,与直觉相反,一个模型的参数的数量与其过拟合之间并没有必然的联系。
相反,一个更成熟的观点是将复杂性等同于假设空间的大小,基于以下事实,较小的假设空间允许由较短的代码表示。像上面的理担保证那节提到的边界可能被视为在暗示更短的假设泛化的更好。这还可以通过给有一些先验偏好空间中的假设分配更短的代码做进一步改善。但是,如果把这看作准确性和简单性之间权衡的“证明”,这就是是循环论证了:我们更喜欢简单的假设,如果它们是准确的,那是因为我们的偏好是准确的,而并不是因为这些假设在我们选择的表述中是“简单”。
11.可表示并不意味着可学习
本质上,用于大小可变的学习器的所有表示都具有形式为“每个函数都可以被表示,或者以无限接近的方式近似被表示”的相关定理。正因如此,某种表示方法的忠实使用者经常忽视所有其他的方法。然而,仅仅因为一个函数可以被表示并不意味着它是可以被学习的。例如,标准的决策树学习器并不能学习出比其训练样本更多的叶子节点。 在连续空间中,使用一组固定的基元来表示很简单的函数通常都需要无限数量的项来表示。

而且,如果假设空间具有许多评价函数的局部最优值,那么往往是这样,学习器即使可以表示,也很可能找不到真正的函数。对于有限的数据,时间和内存,标准学习器只能学习所有可能函数的很小一部分子集,这些子集对于学习器来说会随着表示方法的不同而改变。 因此,关键问题不是“它能否被表示”,答案往往是无关紧要的,而是“它能否被学习?”而且这让我们去尝试不同的学习器(也可能是把它们结合起来)是值得的。
12.相关并不意味着因果
相关并不意味着因果这一点经常被提起,就不值得在这里做过多地说明了。但是,尽管我们所讨论的那种学习器只能学习相关性,但他们的结果往往被视为代表因果关系。这么做是错的吗?如果是,那么人们为什么都这样做呢?
 相关不意味因果
相关不意味因果
往往学习预测模型的目标是用它们作为行动的指南。 如果我们发现啤酒和尿布经常在超市中被一起购买,那么也许把啤酒放在尿布旁边就会增加销量。但除非真正的做实验,否则很难说明这一点。机器学习通常被应用在观测数据上。 一些学习算法可以潜在地从观测数据中提取因果信息,但是它们的适用性相当有限。另一方面,相关性是一个潜在的因果关系的标志,我们可以用它作为进一步考察的指导。
结论
像任何学科一样,机器学习有许多“民间智慧”在书本上很难了解到,但这些知识对成功运用机器学习来说至关重要。多明戈斯教授的论文总结了其中几条最重要的内容。