from Wiki
概述
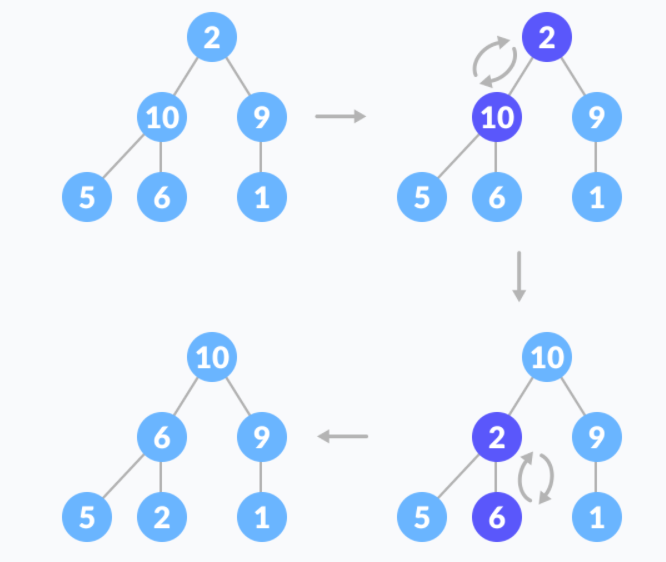
若以升序排序说明,把数组转换成最大堆(Max-Heap Heap),这是一种满足最大堆性质(Max-Heap Property)的二叉树:对于除了根之外的每个节点i, A[parent(i)] ≥ A[i]。
重复从最大堆取出数值最大的结点(把根结点和最后一个结点交换,把交换后的最后一个结点移出堆),并让残余的堆维持最大堆性质。
堆节点的访问
通常堆是通过一维数组来实现的。在数组起始位置为0的情形中:
- 父节点i的左子节点在位置
;
- 父节点i的右子节点在位置
;
- 子节点i的父节点在位置
;
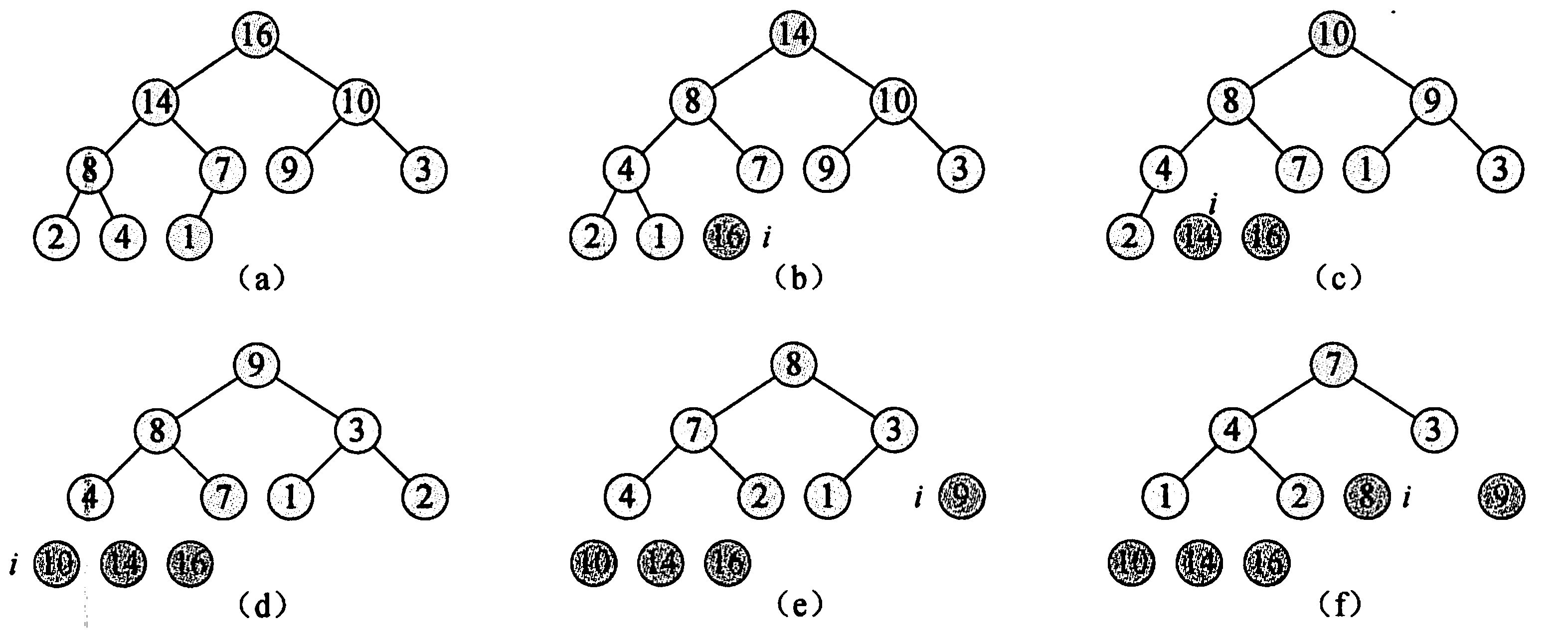
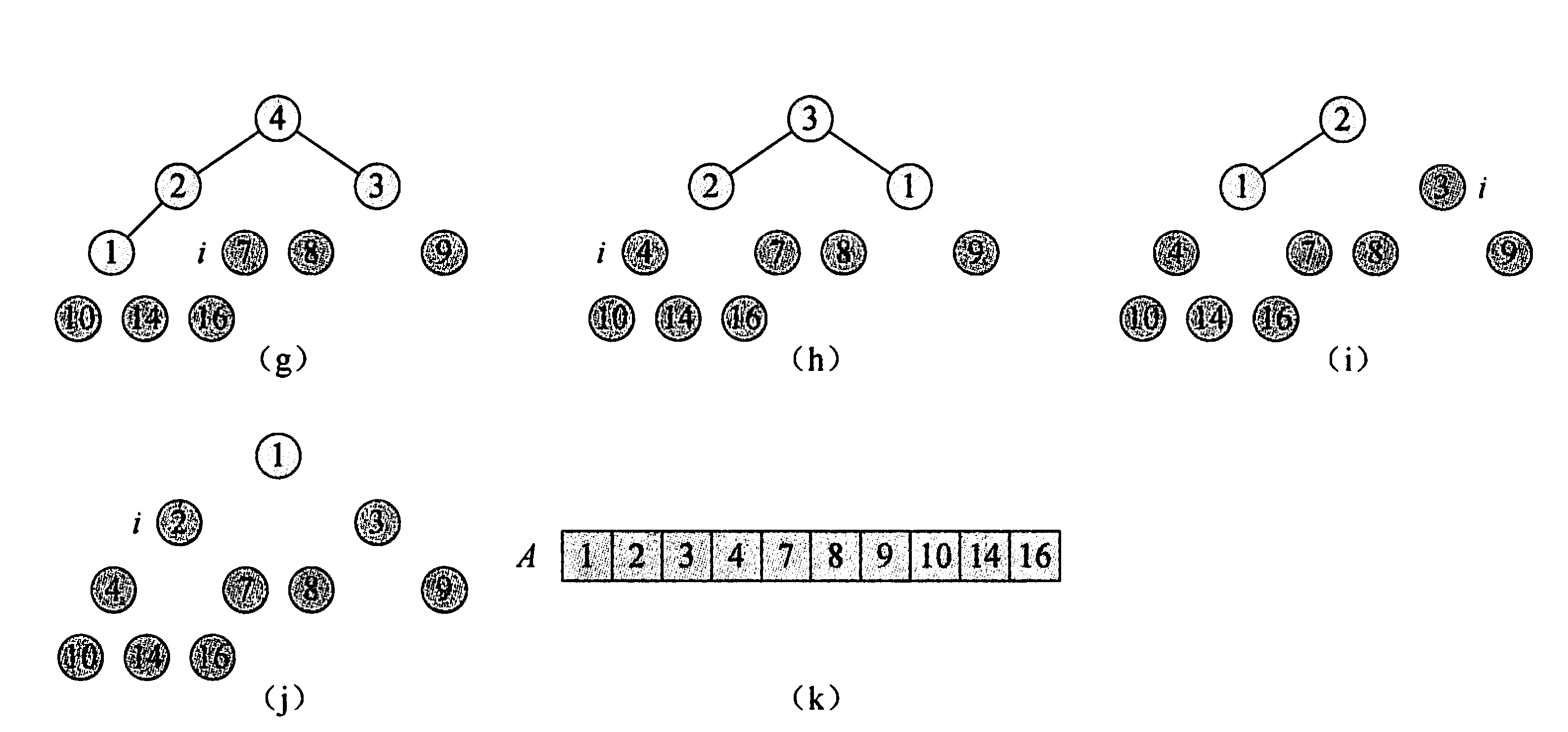
Build max-heap
算法导论 P89
#include"HEAPSORT".h
1 #pragma once 2 #include<vector> 3 //全局静态变量 4 //它与全局变量的区别在于如果程序包含多个文件的话, 5 //它作用于定义它的文件里,不能作用到其它文件里, 6 //即被static关键字修饰过的变量具有文件作用域。 7 //这样即使两个不同的源文件都定义了相同名字的静态全局变量,它们也是不同的变量。 8 static int heap_size; 9 10 //近似完全二叉树:节点i的父节点、左孩子、右孩子 11 //默认向偶数(向下)取整 ----《深入理解计算机系统》 12 //以0起始数组 13 int parent(const int& i) 14 { 15 return (i - 1) / 2; 16 } 17 int left(const int& i) 18 { 19 return 2 * i + 1; 20 } 21 int right(const int& i) 22 { 23 return 2 * i + 2; 24 } 25 //化为最大堆:父节点>左孩子>右孩子 i为父节点 26 void Max_Heapify(std::vector<int>& A, const int& i) 27 { 28 int l = left(i); 29 int r = right(i); 30 int largest; 31 //寻找该节点结构(父、左、右)中最大值 32 if (l <= heap_size && A[i] < A[l]) 33 largest = l; 34 else 35 largest = i; 36 if (r <= heap_size && A[largest] < A[r]) 37 largest = r; 38 //使最大值为父节点 39 if (largest != i) 40 { 41 std::swap(A[i], A[largest]); 42 //使被交换的结点结构也是最大堆 43 Max_Heapify(A, largest); 44 } 45 } 46 47 //建堆:从下到上 48 void Build_Max_Heap(std::vector<int>& A) 49 { 50 // A[n/2]+1+...+n都是含有孩子的父节点 51 for (int i = (A.size()-1) / 2; i >= 0;--i) 52 Max_Heapify(A, i); 53 } 54 55 void HeapSort(std::vector<int>& A) 56 { 57 heap_size = A.size() - 1; 58 Build_Max_Heap(A); 59 //倒数第二个最大堆化:这时就剩下根节点A[0]和该节点i 再次进行最大堆后顺序已定 60 for (int i = A.size() - 1; i != 0;--i) 61 { 62 std::swap(A[0], A[i]);//最大堆化后A[i]为最大值 :排在末尾 63 --heap_size; 64 Max_Heapify(A, 0); 65 } 66 }
main.cpp
#include<iostream> #include<iterator> //ostream_iterator #include"HEAPSORT.h" using namespace std; void print(vector<int>& v) { ostream_iterator<int> out_iter(cout, " "); copy(v.begin(), v.end(), out_iter); } void HeapSort() { vector<int> v = {4,1,3,2,16,9,10,14,8,7}; print(v); cout << endl; HeapSort(v); cout << "heap_soted: " << endl; print(v); } int main() { HeapSort(); }