圆方树

例题

• 树有很多优秀的性质，我们可以把仙人掌图转成一颗树
• 回顾一下点双联通分量：不存在割点的图
• 建一个新图，我们把一个点双看作一个方点，与点双里的每个圆点相连，就形成了一颗圆方树。
• 画个图

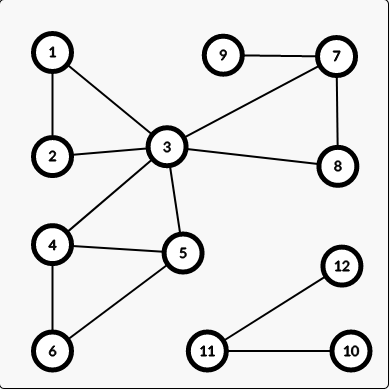  • 原图 圆方树图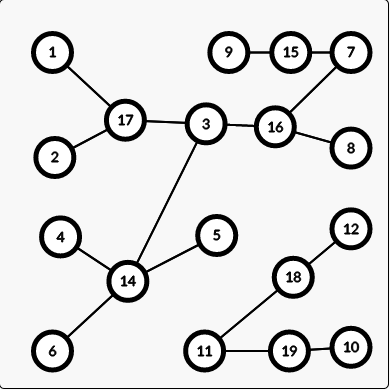

  • code

    void Tarjan(int x) {
        dfn[x] = low[x] = ++dfc;
        stk[++tp] = x;
        for (int i = head[x]; i; i = e[i].next) {
            int y = e[i].t;
            if (!dfn[y]) {
                Tarjan(y);
                low[x] = min(low[x], low[y]);
                if (dfn[x] == low[y]) {
                    ++cnt;
                    while (1) {
                        int z = stk[tp--];
                        rs[cnt].push_back(z);
                        rs[z].push_back(cnt);
                        if (z == y) break;
                    }
                    rs[cnt].push_back(x);
                    rs[x].push_back(cnt);
                }
            }
            else low[x] = min(low[x], dfn[y]);
        }
    }
    

例题

• 压力

  • 如今,路由器和交换机构建起了互联网的骨架。处在互联网的骨干位置的核心路由器典型的要处理100Gbit/s的网络流量。他们每天都生活在巨大的压力之下。
  • 小强建立了一个模型。这世界上有N个网络设备,他们之间有M个双向的链接。这个世界是连通的。在一段时间里,有Q个数据包要从一个网络设备发送到另一个网络设备。
  • 一个网络设备承受的压力有多大呢?很显然,这取决于Q个数据包各自走的路径。不过,某些数据包无论走什么路径都不可避免的要通过某些网络设备。
  • 你要计算:对每个网络设备,必须通过(包括起点、终点)他的数据包有多少个?

• 输入格式

  • 第一行包含3个由空格隔开的正整数N,M,Q。
  • 接下来M行,每行两个整数u,v,表示第u个网络设备(从1开始编号)和第v个网络设备之间有一个链接。u不会等于v。两个网络设备之间可能有多个链接。
  • 接下来Q行,每行两个整数p,q,表示第p个网络设备向第q个网络设备发送了一个数据包。p不会等于q。

• 输出格式

  • 输出N行,每行1个整数,表示必须通过某个网络设备的数据包的数量。

• 样例

  • 样例输入

  • 4 4 2
    1 2
    1 3
    2 3
    1 4
    4 2
    4 3
    

  • 样例输出

  • 2
    1
    1
    2
    

• 数据范围与提示

  • 样例解释

    • 设备1、2、3之间两两有链接,4只和1有链接。4想向2和3各发送一个数据包。显然,这两个数据包必须要经过它的起点、终点和1。

  • 数据规模和约定

    • 对于40%的数据,N,M,Q≤2000
    • 对于60%的数据,N,M,Q≤40000
    • 对于100%的数据,N≤100000,M,Q≤200000

• 解题思路

  • 建圆方树，用倍增求Lca，进行树上差分，最后Dfs求解
  • code

    #include <cstdio>
    #include <vector>
    #include <algorithm>
    using namespace std;
    const int N = 1e5 + 5;
    struct side {
        int t, next;
    }e[N<<1];
    int head[N], tot;
    void Add(int x, int y) {
        e[++tot] = (side) {y, head[x]};
        head[x] = tot;
    }
    vector<int> rs[N<<1];
    int dfn[N], low[N], dfc, cnt, stk[N], tp;
    void Tarjan(int x) {
        dfn[x] = low[x] = ++dfc;
        stk[++tp] = x;
        for (int i = head[x]; i; i = e[i].next) {
            int y = e[i].t;
            if (!dfn[y]) {
                Tarjan(y);
                low[x] = min(low[x], low[y]);
                if (dfn[x] == low[y]) {
                    ++cnt;
                    while (1) {
                        int z = stk[tp--];
                        rs[cnt].push_back(z);
                        rs[z].push_back(cnt);
                        if (z == y) break;
                    }
                    rs[cnt].push_back(x);
                    rs[x].push_back(cnt);
                }
            }
            else low[x] = min(low[x], dfn[y]);
        }
    }
    int f[N<<1][21], d[N<<1];
    void P_lca(int x, int fa) {
        d[x] = d[fa] + 1;
        f[x][0] = fa;
        for (int i = 0; f[x][i]; ++i)
            f[x][i+1] = f[f[x][i]][i];
        for (int i = 0; i < rs[x].size(); ++i)
            if (rs[x][i] != fa) P_lca(rs[x][i], x);
    }
    void Jump(int &x, int d) {
        int k = 0; 
        while (d) {
            if (d & 1) x = f[x][k];
            d >>= 1; k++;
        }
    }
    int Lca(int x, int y) {
        if (d[x] < d[y]) swap(x, y);
        Jump(x, d[x] - d[y]);
        if (x == y) return x;
        for (int i = 20; i >= 0; --i)
            if (f[x][i] != f[y][i])
                x = f[x][i], y = f[y][i];
        return f[x][0];
    }
    int n, m, Q, w[N<<1];
    void Dfs(int x) {
        for (int i = 0; i < rs[x].size(); ++i) {
            int y = rs[x][i];
            if (y == f[x][0]) continue;
            Dfs(y);
            w[x] += w[y];
        }
    }
    int main() {
        scanf("%d%d%d", &n, &m, &Q);
        cnt = n;
        while (m--) {
            int x, y;
            scanf("%d%d", &x, &y);
            Add(x, y); Add(y, x);
        }
        Tarjan(1);
        P_lca(1, 0);
        while (Q--) {
            int x, y, lca;
            scanf("%d%d", &x, &y);
            lca = Lca(x, y);
            w[x]++; w[y]++; w[lca]--; w[f[lca][0]]--;
        }
        Dfs(1);
        for (int i = 1; i <= n; ++i)
            printf("%d
    ", w[i]);
        return 0;
    }