zoukankan html css js c++ java

【CSAPP笔记】1. 位、字节、整型

《Computer Systems a Programmer’s Perspective》，机械工业出版社。中文译名《深入理解计算机系统》。作者：（美）Randal E.Bryant / David O'Hallaron

想写点推荐理由，作罢，原因是自己学识尚浅（留坑以后写？）。这里附上几个链接，也许你看过之后，也会产生和我一样的想法，阅读这本计算机界的经典著作。

以下是正文

程序的结构和执行

这是本书的第一部分，Program Structure and Execution。包括内容是第二到第六章。第二章的标题是：信息的表示和处理（Representing and Manipulating Information）

位、字、数据类型

位

对于有十个手指头的人类来说，使用十进制表示法是很自然的事情，但是当构造处理信息的机器时，二进制的值工作得更好。……这些微不足道的二进制数字，或者成为位（bit），奠定了数字革命的基础

现代计算机的处理、存储的信息以二进制表示。甚至可以说计算机的一切就是0和1。一个bit就是一个0或1。那为什么就偏偏是二进制而不是我们常用的十进制，或者什么三进制五进制之类？简单来说还是离散信号和模拟信号的区别。简言之，0和1这种离散值在用机器来表示时是非常方便的，例如高低电平、纸条带上孔的有无等等。而且模拟信号（如电压）有诸如很容易受其他条件干扰，很容易产生误差这样的缺点，离散数值的优势就体现了。如果说，一个单独的位，只能代表0或1，起不了多大的作用。但如果有很多的位（足够数量），并且对二进制数字串进行一定形式的编码（例如IEEE浮点规则、ASCII码等等），那么我们能赋予一串二进制数一定的意义，让其具有存储、处理信息的能力。虽然0和1是离散的，但大量的0和1，足够让我们认为是“连续”的。此时，二进制数就会向我们展示它的魔力。

十进制0~15的三种进制表示

十六进制	十进制	二进制	十六进制	十进制	二进制
0	0	0000	8	8	1000
1	1	0001	9	9	1001
2	2	0010	A	10	1010
3	3	0011	B	11	1011
4	4	0100	C	12	1100
5	5	0101	D	13	1101
6	6	0110	E	14	1110
7	7	0111	F	15	1111

这张表需要熟悉，也就是要了解进制转换的一些规则。

字

8个bit是一个字，或者叫做字节（byte）。字节是作为最小的可寻址存储器单位（并不是一个个位去存储和访问）。每个字节都有一个唯一的数字作为标识，这个数字就是地址（Address）

计算机有一个很重要的概念叫做字长（word size），指明整数和指针的标称大小。因为一个个地址都是唯一的数字，就是由一个字编码的。所以字长决定的一个最重要的系统参数就是虚拟地址空间的最大大小。一般来说32位的计算机，限定虚拟地址空间为4GB（2的32次方减1个字节）。

C语言数据类型的字节数

大端法、小端法

测试代码如下：

#include<stdio.h>
typedef unsigned char *byte_pointer;

void show_bytes(byte_pointer start, int len) {
	int i;
	for (i = 0; i < len; i++)
		printf(" %.2x", start[i]);
	printf("
");
}

void show_int(int x) {
	show_bytes((byte_pointer)&x, sizeof(int));
}

int main()
{
	int x = 12345;
	show_int(x);
	return 0;
}

在显示一个w位的整数时，如果w是8的整数，那么能以字节为单位来表示。最低有效字节排在前面的方式叫做小端法，大多intel兼容机器采取小端法。大端法采用的是最高有效字节在最前面，也就是我们平常习惯的方式。例如12345的32位编码是0000 3039。小端法是如下的输出。

bool代数、逻辑运算、移位运算

bool代数

位运算

以下是一些补充记录：

掩码运算。按位与：&，常用于保持某位不变（x&1），或把某些位置为0（x&0）。按位或：|，常用于将某些位置置为1（x|1）。
对于逻辑运算来说，0代表“false”，所有的非0值代表“true”。
对于任何值a来说，a ^ a=0，因此有(a ^ b) ^ a=b ，加以利用可以带来有趣的结果。例如：a是密钥，b是明文，a^b是加密，加密后的值就被保护。想要知道明文，只能用a去解密
对于右移，<<，机器支持两种模式的右移。
- 逻辑右移，右移后在左端补0。
- 算术右移，右移后在左端补最高有效位的值。
- 例如对于 x = 0x10010011，x =<< 4; 如果是逻辑右移，结果为 x = 00001001；如果为算术右移，结果为11111001。
移位数量应该保持小于字长。
加减法优先级比移位高。

2017/03/14 update：关于位运算符放一张很久之前整理的表格：

整数（integer）表示

整数编码

整数分为有、无符号两种类型，（unsigned）。根据字节数的不同还分为char、short、int、long、long long。

对于整数的编码，简言之，就是每个位上面的值乘以该位对应的权值，再求和。

1.无符号数编码（binary to unsigned）

UMax，即编码全为1。
UMin，编码全为0。

2.补码编码（binary to Two’s compliment），与unsigned的区别在于最高有效位解释为负权

TMax，符号位为0，剩下位全为1。
TMin，符号位为1，剩下位全为0。
求一个有符号数的负数（补码的逻辑运算非），可以理解为把全部位取反后，对结果再加1。特别地，TMin的“负数”依然是TMin。

C语言默认是有符号整型。如果想要无符号常数，需要加关键词U做限制。

无符号数和有符号数之间的转换

关键点：同样字长的有符号数和无符号数，使用的是相同的位模式。

难点：C语言中，对于一个运算，如果一个运算数是有符号的，另一个是无符号的，那么C语言会隐式地将有符号参数强制类型转换成无符号数，并且假设这两个数是非负的。因此，会导致一些奇怪的结果。例如：

对于第一个式子来说，由于一个操作数是有符号，另一个操作数是无符号，那么有符号数-1被强制转换成一个无符号数，会变成一个很大的无符号数。

第二个，-2147483647-1 其实就是头文件<limit.h>中32位补码TMin的写法（这是由于C语言规则所致）。转换成无符号之后的值要比TMax大1。

第三个，这两个操作数都是有符号型，而且2147483648大于TMax，导致溢出，成了一个很小的负数。

扩展、截断

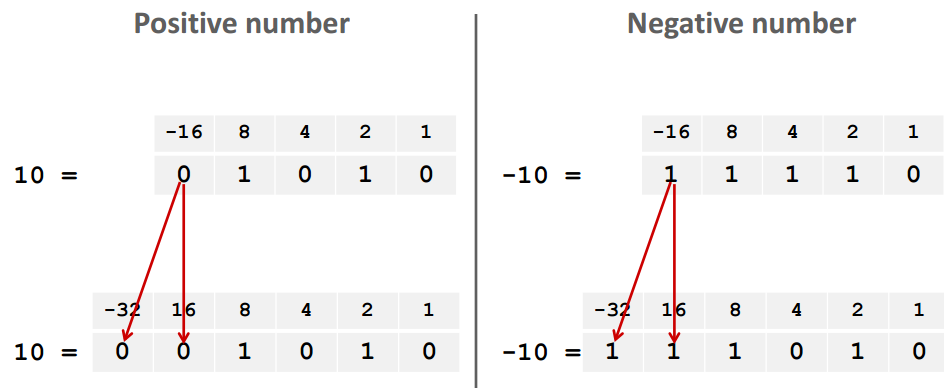
#include<stdio.h>
typedef unsigned char *byte_pointer;

void show_bytes(byte_pointer start, int len) {
	int i;
	for (i = 0; i < len; i++)
		printf(" %.2x", start[i]);
	printf("
");
}

void show_int(int x) {
	show_bytes((byte_pointer)&x, sizeof(int));
}

void show_short(short x) {
	show_bytes((byte_pointer)&x, sizeof(short));
}

int main()
{
	//扩展
	short x = 12345;
	show_short(x);
	printf("short x = %d
", x);
	show_int(x);
	printf("int x = %d

", (int)x);

	//截断
	int y = 123456;
	show_int(y);
	printf("int y = %d
", y);
	show_short(y);
	printf("short y = %d

", (short)y);
	return 0;
}

扩展，例如short到int，int到long long int这样。不会改变数字的值。如果是无符号数就是扩展全部为0的位，有符号数就是扩展全部为1的位。

截断，例如int到short，有点类似于右移，类似于mod 2的n次方，但只是类似。对于大的数据，截断会导致溢出。例如int型整数123456大于short能表示的最大数值范围，如果将其截断会导致上溢出从而得到一个负数。

2017/03/14 update：如果打算通过使用扩展位数的手段来使得一些运算结果由原本的溢出变为不溢出，那么强制类型转换和计算这两个过程的先后顺序很重要。例如下面这个函数验证两个32位的int型整数做乘法有没有产生溢出，验证的手段是先用64位的整型存结果，再将64位乘积截断为32位是否会改变其值：

int imull(int x, int y){
    long long pll = (long long)x * y;
    return pll == (int)pll;
}

代码第二行的强制类型转换至关重要，先转换再计算。如果第二行是这么写的话：

long long pll = x * y;

那么会用32位值来计算乘积（可能这会溢出），然后再将其扩展为64位。显然不会达到目的。可以参考下面的运行结果