POJ

Given a n × n matrix A and a positive integer k, find the sum S = A + A² + A³ + … + A^k.

Input

The input contains exactly one test case. The first line of input contains three positive integers n (n ≤ 30), k (k ≤ 10⁹) and m (m < 10⁴). Then follow n lines each containing n nonnegative integers below 32,768, giving A’s elements in row-major order.

Output

Output the elements of S modulo m in the same way as A is given.

Sample Input

2 2 4
0 1
1 1

Sample Output

1 2
2 3

思路，把矩阵看成一个数字。

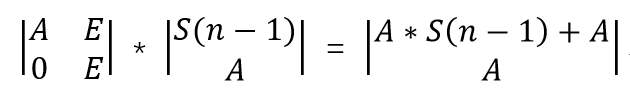
#include<iostream>
#include<algorithm>
#include<vector>
#include<stack>
#include<queue>
#include<map>
#include<set>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<ctime>
#define fuck(x) cout<<#x<<" = "<<x<<endl;
#define debug(a,i) cout<<#a<<"["<<i<<"] = "<<a[i]<<endl;
#define ls (t<<1)
#define rs ((t<<1)+1)
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int maxn = 100086;
const int maxm = 100086;
const int inf = 2.1e9;
const ll Inf = 999999999999999999;
//const int mod = 1000000007;
const double eps = 1e-6;
const double pi = acos(-1);

int n,k,mod;

struct Matrix{
    int mp[70][70];
};
Matrix a;


Matrix mul(Matrix a,Matrix b,int n){
    Matrix ans;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            ans.mp[i][j]=0;
            for(int k=1;k<=n;k++){
                ans.mp[i][j]+=a.mp[i][k]*b.mp[k][j];
            }
            ans.mp[i][j]%=mod;
        }
    }
    return ans;
}

Matrix q_pow(Matrix a,int b,int n){
    Matrix ans;
    memset(ans.mp,0,sizeof(ans.mp));
    for(int i=1;i<=n;i++){
        ans.mp[i][i]=1;
    }
    while (b){
        if(b&1){
            ans=mul(ans,a,n);
        }
        b>>=1;
        a=mul(a,a,n);
    }
    return ans;
}

Matrix mul1(Matrix a,Matrix b,int n){
    Matrix ans;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            ans.mp[i][j]=0;
            for(int k=1;k<=n;k++){
                ans.mp[i][j]+=a.mp[i][k+n]*b.mp[k][j];
            }
            ans.mp[i][j]%=mod;
        }
    }
    return ans;
}

int main()
{
    scanf("%d%d%d",&n,&k,&mod);
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            scanf("%d",&a.mp[i][j]);
            a.mp[i][j]%=mod;
        }
    }
    for(int i=1;i<=n;i++){
        a.mp[i][i+n]=1;
        a.mp[i+n][i+n]=1;
    }
    Matrix tmp=q_pow(a,k-1,n*2);
    Matrix b=tmp;
    tmp = mul(tmp,a,n);
    a=mul1(b,a,n);
    for(int i=1;i<=n;i++){
        for(int j=1;j<n;j++){
            printf("%d ",(tmp.mp[i][j]+a.mp[i][j])%mod);
        }
        printf("%d
",(tmp.mp[i][n]+a.mp[i][n])%mod);
    }
    return 0;
}