带花树是一种解决一般图上的最大匹配问题的一种算法。
参考:http://www.cnblogs.com/cjyyb/p/8719368.html
我们在一般在做最大匹配的时候都会先二分图染色,然而如果图中有奇数边环的话就GG了。
所以带花树是用来处理奇环的。
其实它和匈牙利算法本质上差不太多。
首先,我们不用dfs进行增广,而使用bfs。
在bfs的过程中,我们要对这张图进行染色。
令匹配点颜色为1(黑),被匹配点颜色为2(白).
现在我们正在遍历边u->v,其中u是匹配点。
假如u和v已经被标记在了一个奇数环内或者v已经被染色,那么就不用管了。
假如v没有被染色,就把v然乘被匹配点,连pre边,pre[v]=u。
这时如果v已经被匹配了,那么我们就把v的匹配点加入队列。
否则说明我们这一轮增广成功了,把之前的改掉就好了。
这其实和匈牙利算法一模一样。
大概这么实现
for(int now=v,pr;now;now=pr) pr=match[pre[now]],match[now]=pre[now],match[pre[now]]=now;
然后我们最不愿意看到的情况就是v是一个黑点,说明此时出现了奇数环。
我们分析一下这个奇数环,假设它的长度为2*k+1,那么它里面已经有了k组匹配和一个单点,那么如果这个环对本轮增广有贡献的话,一定是某个点匹配上了环外的一个点。
所以我们有结论,环上的所有点是等价的,我们需要把它们缩成一个点。
怎么缩呢?
我们现在的奇环是长这样的。
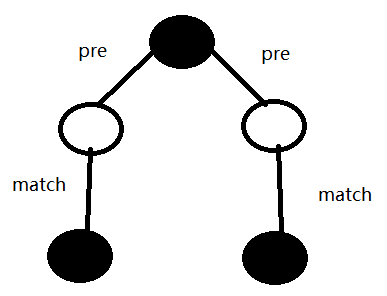
pre边和match边是交替出现的,而且这个环的LCA一定是一个黑点。
所以我们就暴力向上跳黑点,找到LCA,然后把所有点用并查集并到LCA上。
再把所有白点染黑并加入队列尝试增广。
这大概是这个算法的全过程。
为了算法的正确性,我们每次尝试增广之后都要重置pre和并查集,还有染色的结果。
复杂度:n^3。
例题
[WC2016]挑战NPC
小 N 最近在研究 NP 完全问题,小 O 看小 N 研究得热火朝天,便给他出了一道这样的题目:
有 n 个球,用整数 1 到 n 编号。还有 m 个筐子,用整数 1 到 m 编号。每个筐子最多能装 3 个球。
每个球只能放进特定的筐子中。 具体有 e 个条件,第 i 个条件用两个整数 vi 和 ui 描述,表示编号为 vi 的球可以放进编号为 ui 的筐子中。
每个球都必须放进一个筐子中。如果一个筐子内有不超过 1 个球,那么我们称这样的筐子为半空的。
求半空的筐子最多有多少个,以及在最优方案中, 每个球分别放在哪个筐子中。
小 N 看到题目后瞬间没了思路,站在旁边看热闹的小 I 嘿嘿一笑:“水题!” 然后三言两语道出了一个多项式算法。
小 N 瞬间就惊呆了,三秒钟后他回过神来一拍桌子:“不对!这个问题显然是 NP 完全问题,你算法肯定有错!”
小 I 浅笑:“所以,等我领图灵奖吧!”
小 O 只会出题不会做题,所以找到了你——请你对这个问题进行探究,并写一个程序解决此题。
题解
考虑为什么要设置成三个点?而合法条件是0个或一个。
三个点完全图的最大匹配为1,两个点为1,一个点或0个点为0.
所以上放了0个或1个时,空闲位置有两个或三个,刚好能形成一组匹配。
所以我们把一个框拆成三个,小球直接连边,三个筐之间也连边。
答案为最大匹配-球数。
代码
#include<iostream> #include<cstdio> #include<queue> #include<cstring> #define N 602 using namespace std; queue<int>q; int f[N],tot,head[N],pre[N],n,tim,dfn[N],match[N],m,ans,vis[N],T,cnt,be[N],id[N][4],k; inline int rd(){ int x=0;char c=getchar();bool f=0; while(!isdigit(c)){if(c=='-')f=1;c=getchar();} while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=getchar();} return f?-x:x; } struct edge{ int n,to; }e[N*N*2]; inline void add(int u,int v){ e[++tot].n=head[u];e[tot].to=v;head[u]=tot; e[++tot].n=head[v];e[tot].to=u;head[v]=tot; } int find(int x){return f[x]=f[x]==x?x:find(f[x]);} inline int getlca(int u,int v){ ++tim;u=find(u);v=find(v); while(dfn[u]!=tim){ dfn[u]=tim; u=find(pre[match[u]]); if(v)swap(u,v); } return u; } void bloom(int x,int y,int lca){ while(find(x)!=lca){ pre[x]=y;y=match[x]; if(vis[y]==2)vis[y]=1,q.push(y); if(find(x)==x)f[x]=lca; if(find(y)==y)f[y]=lca; x=pre[y]; } } int work(int s){ for(int i=1;i<=cnt;++i)pre[i]=vis[i]=0,f[i]=i; while(!q.empty())q.pop();q.push(s);vis[s]=1; while(!q.empty()){ int u=q.front();q.pop(); for(int i=head[u];i;i=e[i].n){ int v=e[i].to; if(find(u)==find(v)||vis[v]==2)continue; if(!vis[v]){ vis[v]=2;pre[v]=u; if(!match[v]){ for(int now=v,pr;now;now=pr) pr=match[pre[now]],match[now]=pre[now],match[pre[now]]=now; return 1; } vis[match[v]]=1;q.push(match[v]); } else{ int lca=getlca(u,v); bloom(u,v,lca);bloom(v,u,lca); } } } return 0; } inline void unit(){ memset(match,0,sizeof(match));ans=0; memset(head,0,sizeof(head));tot=0; } int main(){ T=rd(); while(T--){ unit(); n=rd();m=rd();k=rd();cnt=n; int u,v; for(int i=1;i<=m;++i){ for(int j=1;j<=3;++j)id[i][j]=++cnt,be[cnt]=i; add(cnt-1,cnt);add(cnt-2,cnt);add(cnt-1,cnt-2); } for(int i=1;i<=k;++i){ u=rd();v=rd(); add(u,id[v][1]);add(u,id[v][2]);add(u,id[v][3]); } for(int i=1;i<=cnt;++i)if(!match[i])ans+=work(i); printf("%d ",ans-n); for(int i=1;i<=n;++i)printf("%d ",be[match[i]]);puts(""); } return 0; }