邻接数组表示法
邻接数组表示法是以一个n*n的数组来表示一个具有n个顶点的图形。我们以数组的索引值来表示顶点,以数组的内容值来表示顶点间的边是否存在(以1表示存在边;以0表示不存在边)。如图5.12所示的无向图形,其邻接数组为表5.1所示。
表 5.1
| 0 | 1 | 2 | 3 | 4 | |
| 0 | 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 | 1 |
| 2 | 1 | 0 | 0 | 1 | 0 |
| 3 | 1 | 1 | 1 | 0 | 0 |
| 4 | 0 | 1 | 0 | 0 | 0 |
再来看看有向图形的邻接数组如何表示,如图5.13所示。
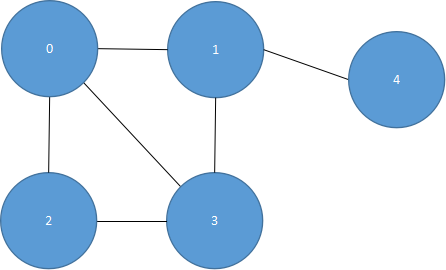
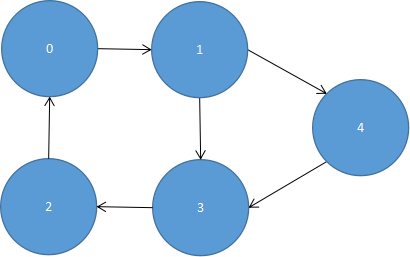
图 5.12 图 5.13
其邻接数组为表5.2所示。
表 5.2
| 0 | 1 | 2 | 3 | 4 | |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 |
| 2 | 1 | 0 | 0 | 0 | 0 |
| 3 | 0 | 0 | 1 | 0 | 0 |
| 4 | 0 | 0 | 0 | 1 | 0 |
邻接列表表示法
邻接列表法是以链表来记录各顶点的邻接顶点。其结点结构如下:

如图5.14所示的有向图形:
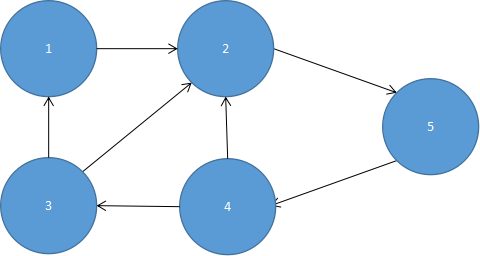
图 5.14
其邻接列表为:
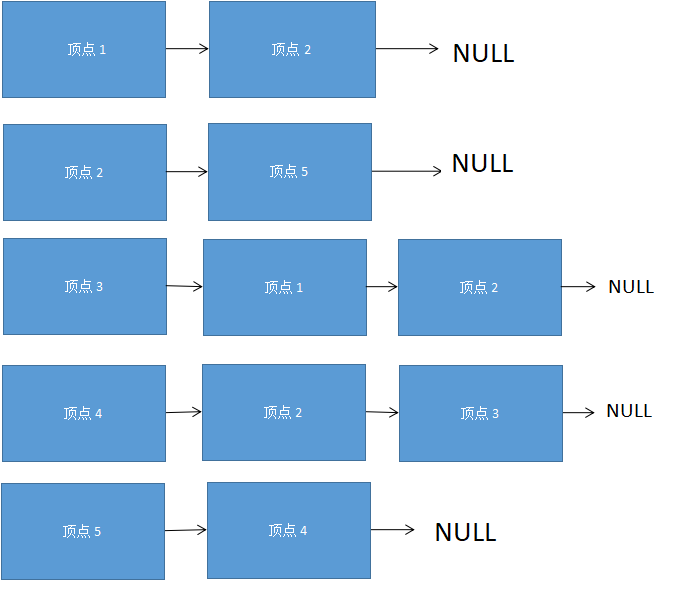
加权边的图形
在七桥问题中,每个桥都是有长度的,为了表示这些信息,我们在图形的边上加上一些数字来表示,这样的图,我们称为“加权边的图形”。例如图5.15就是一个加权边的图形。
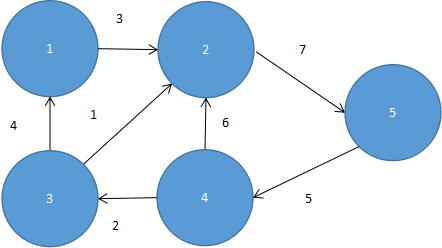
图 5.15
它的邻接数组应该如表5.3这样表示。
表 5.3
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 0 | 3 | 0 | 0 | 0 |
| 2 | 0 | 0 | 0 | 0 | 7 |
| 3 | 4 | 1 | 0 | 0 | 0 |
| 4 | 0 | 6 | 2 | 0 | 0 |
| 5 | 0 | 0 | 0 | 5 | 0 |
如果使用邻接列表来表示图形,则列表的结点必须添加一个记录加权值的字段。加权边的邻接列表结点结构如下:

深度优先法
深度优先法(DFS):
例如对于图5.16所示的无向图形:
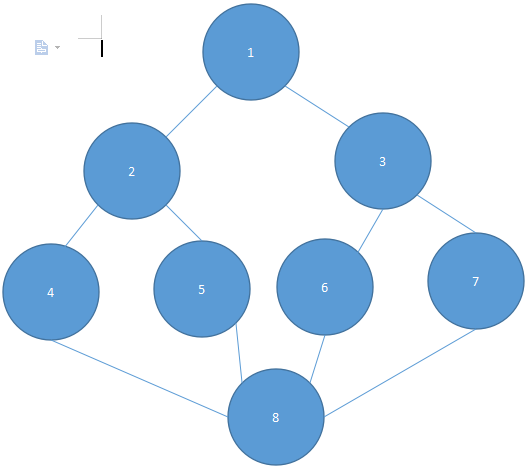
图 5.16
使用深度优先法的过程如下。
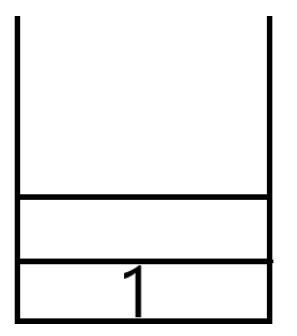
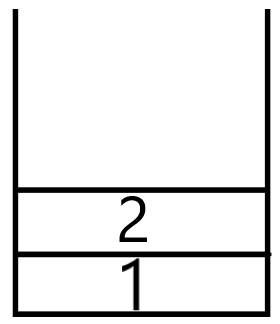
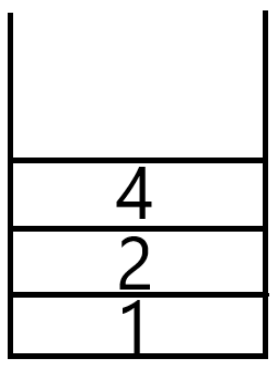
图 5.17 图 5.18 图 5.19
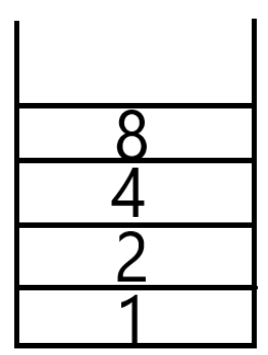
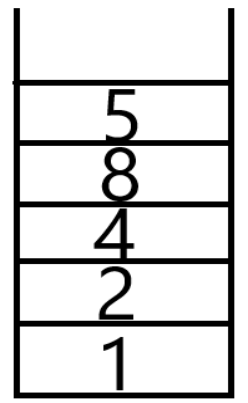
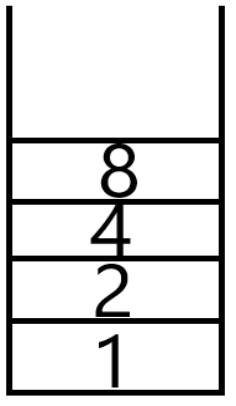
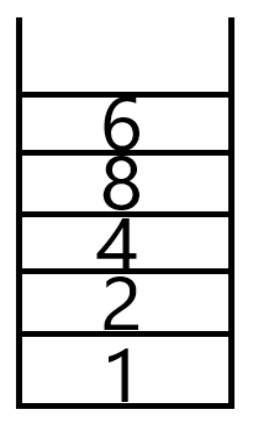
图 5.20 图 5.21 图 5.22 图 5.23
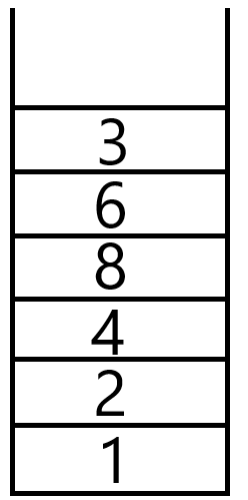


图 5.24 图 5.25 图 5.26
所以查找顺序为:1,2,4,8,5,6,3,7。但因为在深度优先搜索时,可选择同一深度的邻接顶点中的任何一个继续进行深度查找,所以深度优先搜索的顺序并不是唯一的。
广度优先法
广度优先法(BFS)是指在图形中,如果以顶点V作为起始点开始查找,我们从顶点V的邻接列表中选择一个未查找过的顶点W,将顶点V的所有邻接顶点查找过后,再继续对顶点W的所有邻接顶点进行广度优先法的查找,然后再继续查找顶点V的下一个邻接顶点的所有邻接顶点,重复进行广度优先搜索,直到所有的邻接顶点皆查找过为止。通常是使用队列来存储邻接顶点,每查找一个邻接顶点便把其所有的邻接顶点存入队列中,直到队列空了才结束广度优先搜索。
例如图5.28所示的无向图形:
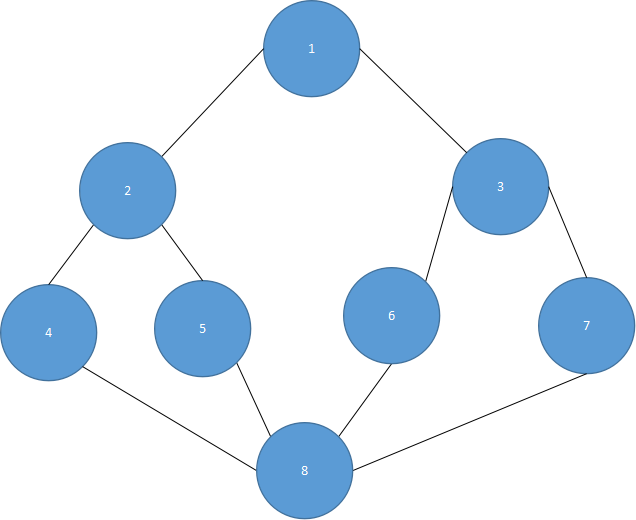
图 5.28









所以查找的顺序为:4,2,8,1,5,6,7,3。而且由于广度优先搜索时,同一广度的邻接顶点,可选择其中一个继续进行邻接顶点的广度查找,因此广度优先搜索的顺序也不是唯一的。
生成树问题
一个图形,如果有N个顶点,则至少要有N-1个边才能将N个顶点给相连起来,形成连通图形。这种用N-1个边的连通图形,我们称为生成树。
例如图5.30所示的无向图形,我们可以以深度优先搜索法或广度优先搜索法生成树。
以顶点1开始的深度优先搜索,所生成的树如图5.31所示。

图 5.30
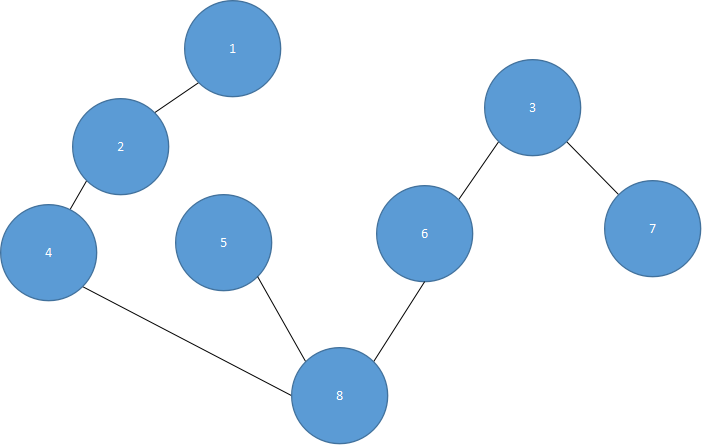
图 5.31
以顶点4开始的广度优先搜索,所生成的树如图5.32所示。
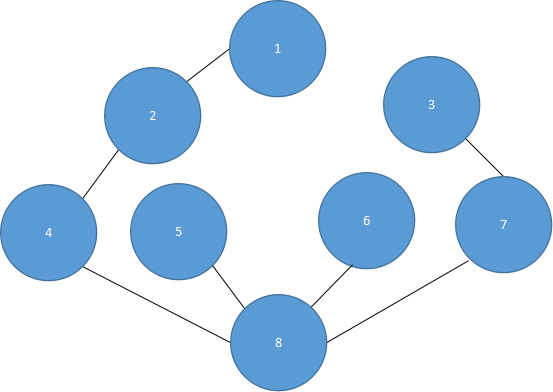
图 5.32
最小生成树(MST):在一个有加权边的图形生成的所有生成树中,加权值总和最小的生成树,我们称为最小生成树。例如:魔法学院有5栋大楼,如图5.33所示,我们需要用网络来连接各栋大楼,已知每栋楼之间的距离,问:怎样连线距离最短?
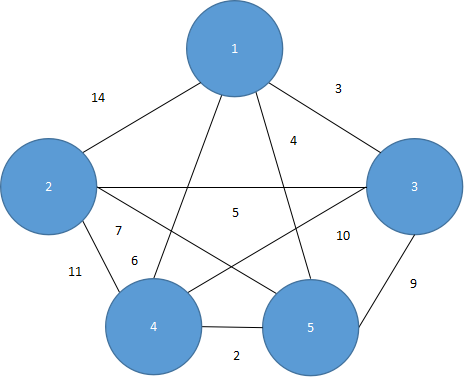
图 5.33
如果我们能够找出这张图形的最小生成树,就可以用最少的网络线连接5栋大楼。
Kruskal算法
Kruskal算法是根据边的加权值以递增的方式,依次找出加权值最低的边来建最小生成树,并且每次添加的边不能造成生成树有回路,直到找到N-1个边为止。当边集比较少时,可考虑用此法。我们以图5.34为例。
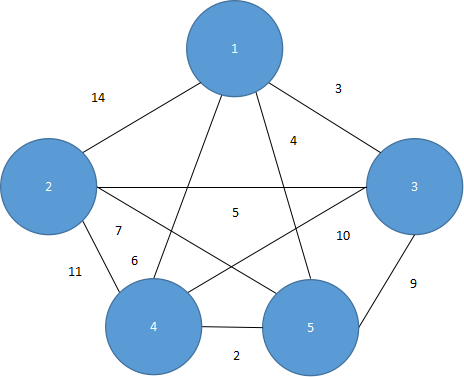
图 5.34
首先将图形中所有的边递增排序(快排),结果如表5.4所示。
表 5.4
| 邻接边 | 4,5 | 1,3 | 1,5 | 2,3 | 1,4 | 2,5 | 3,5 | 3,4 | 2,4 | 1,2 |
| 加权值 | 2 | 3 | 4 | 5 | 6 | 7 | 9 | 10 | 11 | 14 |
第一步,将(4,5)的边加到生成树中,如图5.35所示。
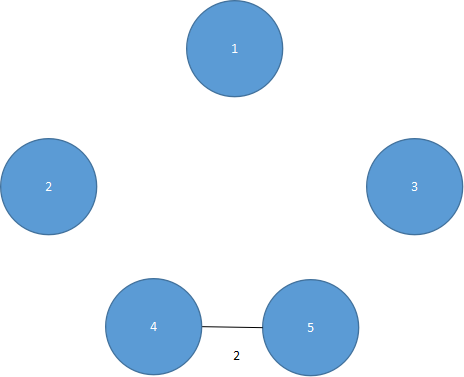
图 5.35
第二步 ,将(1,3)加入生成树中,如图5.36所示。
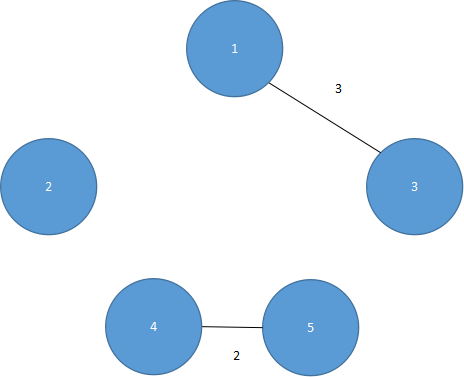
图 5.36
第三步,将(1,5)加入生成树中,如图5.37所示。
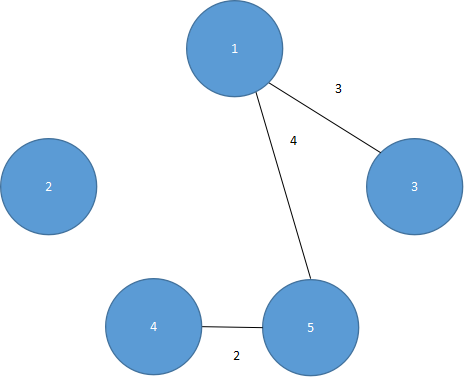
图 5.37
第四步,将(2,3)加入生成树中,如图5.38所示。
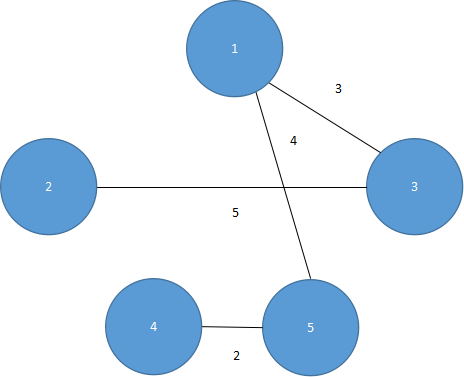
图 5.38
由于共有5个顶点,而现在生成树已达4个边,生成树建立完成。加权值总和为14。
其实这个例子举得并不是十分恰当,容易造成只要排序后加N-1条边就可以的错觉。然而在很多条件下情况并非如此,比如说图5.39所示的这个例子。
这里就需要并查集来判断两个结点是否属于同一棵树从而判断是否应该将这条边加入。
即每加一条边时,你需要考虑:
1. 它是不是剩下边中最小的一条;
2. 加入它会不会造成图的回路。
以图5.40为例。
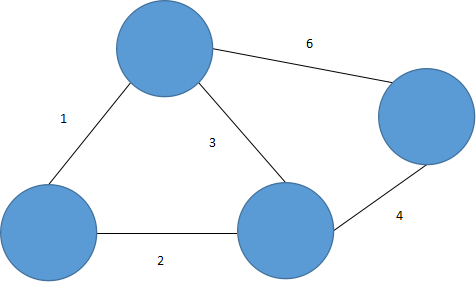
图 5.39
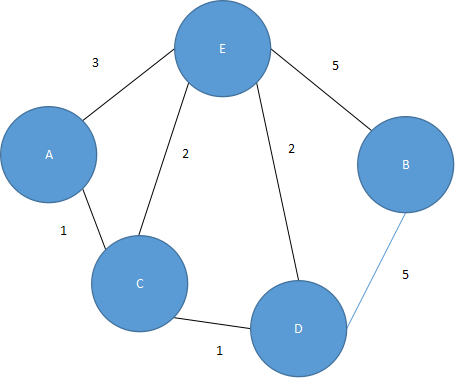
图 5.40
先让每个结点的父结点 father[]=自身编号;
第一次加入(A,C)边,C的父结点设为A;
第二次要加入(C,D)边,D的父结点设置为C,而C的父结点是A,则D的父结点也为A;
第三次加入(C,E)边,同理,E的父结点为A;
第四次要加入(D,E)边,因为D,E的父结点都为A,表示E,D在一个分支中,会形成回路,拒绝加入;
第五次要加入(A,E)边,因为A,E的父结点都为A,拒绝加入;
第六次加入(B,D)边,D的父结点为A。
判断是否为相同集合的代码片段如下。
Prims算法
Prims算法是一种基于“贪心”的求最小树算法,以每次加入一个的邻接边来建立最小生成树,直到找到N-1个边为止。Prims的规则是以开始时生成树的集合为起始的顶点,然后找出与生成树集合邻接的边中,加权值最小的边来生成树,为了确定新加入的边不会造成回路,所以每一个新加入的边,只允许有一个顶点在生成树集合中。重复执行此步骤,直到找到N-1个边为止。
Prims算法适合稠密图,其时间复杂度为O(n^2),其时间复杂度与边的数目无关,而Kruskal算法的时间复杂度为O(eloge),跟边的数目有关,适合稀疏图。我们以图5.41为例:

图 5.41
设数组mincount[],其中mincount[i]表示集合U中的顶点到集合U外的顶点i的最小边权。设mincount[1]=0,则因为mincount[1]=0最小,将顶点1放入集合U={1},此时与集合相邻的边为{(1,2),(1,3),(1,4),(1,5)},更新mincount[2]、mincount[3]、mincount[4]、mincount[5]的值,如图5.42所示。
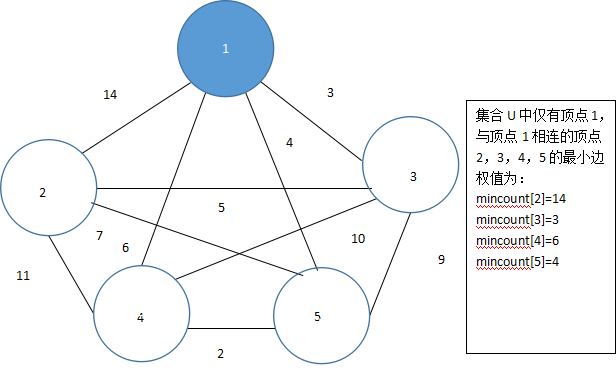
图 5.42
由于mincount[3]=3的值最小,将顶点3加入集合U,即U={1,3},此时与顶点3相邻的顶点为2,4,5,更新mincount[2]、mincount[4]、mincount[5]的值,如图5.43所示。
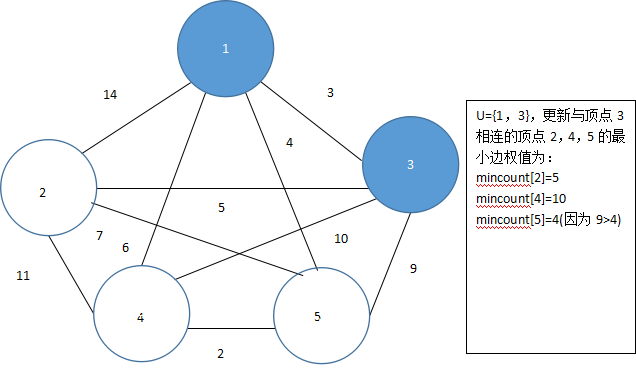
图 5.43
由于mincount[5]=4最小,将顶点5加入集合U,即U={1,3,5},此时与顶点5相邻的顶点为2,4,更新mincount[4]、mincount=[2]的值,如图5.44所示。
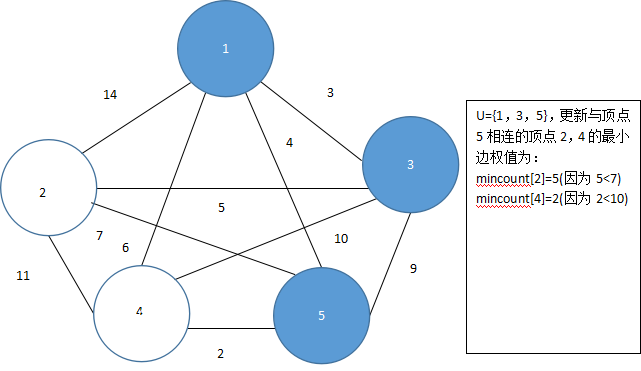
图 5.44
由于mincount[4]=2最小,将顶点4加入集合U,即U={1,3,4,5},此时与顶点4相邻的顶点为2,更新mincount[2]的值,如图5.45所示。
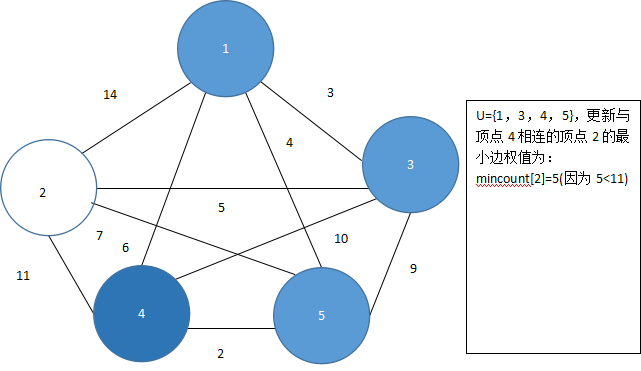
图 5.45
此时仅剩一个顶点2,连接顶点2,如图5.46所示。
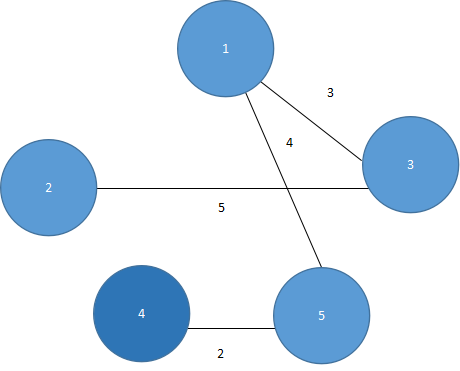
图 5.46
参考程序如下。
Dijkstra算法
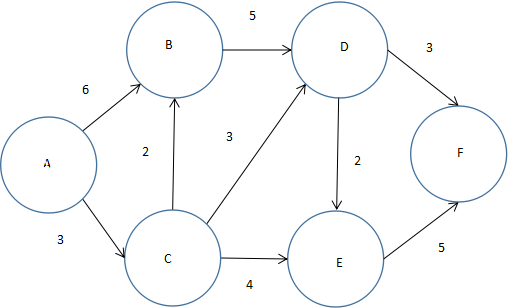
图 5.47
我们在这里可以采用一种叫Dijskstra的算法。Dijkstra算法的规则为:设置顶点集合S,首先将起始点加入该集合,然后根据起始点到其他顶点的路径长度,选择路径长度最小的顶点加入集合,根据所加入顶点更新源点到其他顶点的路径长度,然后再选取最小边的顶点。依次来做,直到求解出到达所有顶点的路径长度。
我们以样例来说明。
首先,将起点A标记为已访问,从A点出发,找出所有和A邻近,且有路径的城市即B和C。我们在B和C上标记现在的路径总和W,则从A到B的总和路径为6,从A到C的总和路径为3。(A点到A点自身为0)如图5.48所示。

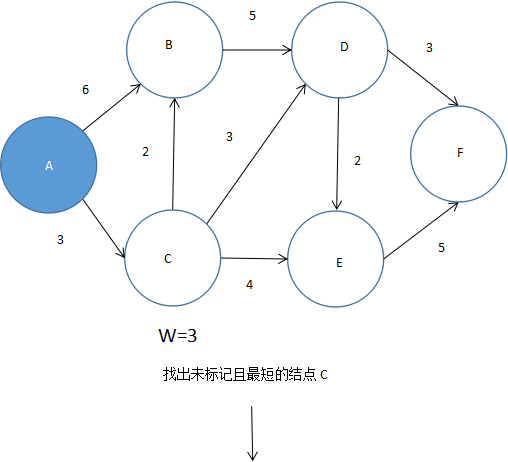

图 5.48
标记C结点为已访问,再从总和路径最短的C出发,找出与C有路径所有未标记结点即D和E,更新A至各未标记结点的最小距离,这时我们会发现,从A经由C到达B的总和路径为5,比A直接到B的路径6还短,所以我们决定选择从A经C到达B,如图5.49所示。
![]()
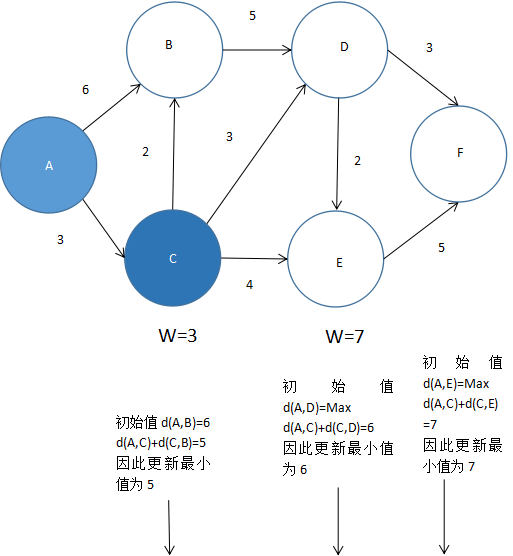

图 5.49
此时未标记且路径最短的结点为B,将B标为已访问,再找到与B点有路径的所有未标记结点即D,更新所有未标记结点的最短路径。可以发现没有值被改变,如图5.50所示。

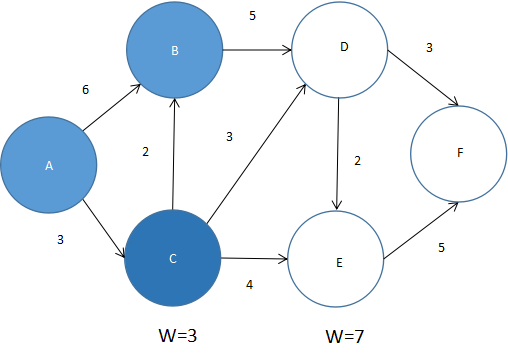

图 5.50
此时未标记且路径最短的结点为D,将D标为已访问,