系统的可靠性:对于系统可靠性的一个计算、度量.第二部分是数据安全与保密,这一部分我们主要要讲到加密,对称加密和非对称加密,以及信息摘要等相关内容.第三点是计算机网络安全.下面我们就看第一个考点.也就是系统可靠性.
系统可靠性模型是一个非常重要的一个知识点.几乎每年都会要考到相关的计算题.
计算机系统的硬件故障通常都是由于元器件的失效而引起的.你比如说主板上面某一个电容、电阻或者是某一个二极管失效了.失效了呢就会影响到整体的一个系统的正确运行,使得计算机系统引发这个硬件故障.那么对元器件进行寿命测试并且根据这个寿命测试进行数据分析,我们就得出了一个结论:就是元器件它的可靠性分为三个阶段:第一个阶段是开始阶段.第二个阶段是正常运行、正常工作的一个阶段.第三个阶段也就是最后一个阶段,是元器件老化的一个阶段.
那么对于三个不同的阶段,我们的处理方式是不同的.然后对于不同的阶段,元器件的这个工作性能它也是不同的.比如说开始阶段,开始阶段的话其实元器件它的工作状态是不够稳定的.所以导致了比较高的失效率.当用过一段时间以后,电气元件它的特性开始稳定下来的时候,器件就进入了正常工作的一个时期.最后呢用了一段时间以后,元器件开始老化,它的出错率、它的失效率也就高了.对于这样的元器件,我们应该将其淘汰.
正是由于这么一个特色,所以这三个阶段,系统可靠性的三个阶段,我们可以用一条曲线来表示.初始阶段呢,出错率比较高,可靠性不够;然而正常工作了一段时间以后,由于元器件的一个损耗,而导致了这个元器件它的失效率又开始增高.像这么一个曲线,我们称为浴盆曲线.很形象,像一个浴盆.那么系统的可靠性呢就是指的从系统开始运行到某一时刻t这一段时间能够正常运行的概率.系统可靠性就是这么一个概念.同时我们的失效率也有了一个定义,失效率是指的单位时间内失效的元件数与元件总数的比例,通常用λ表示.
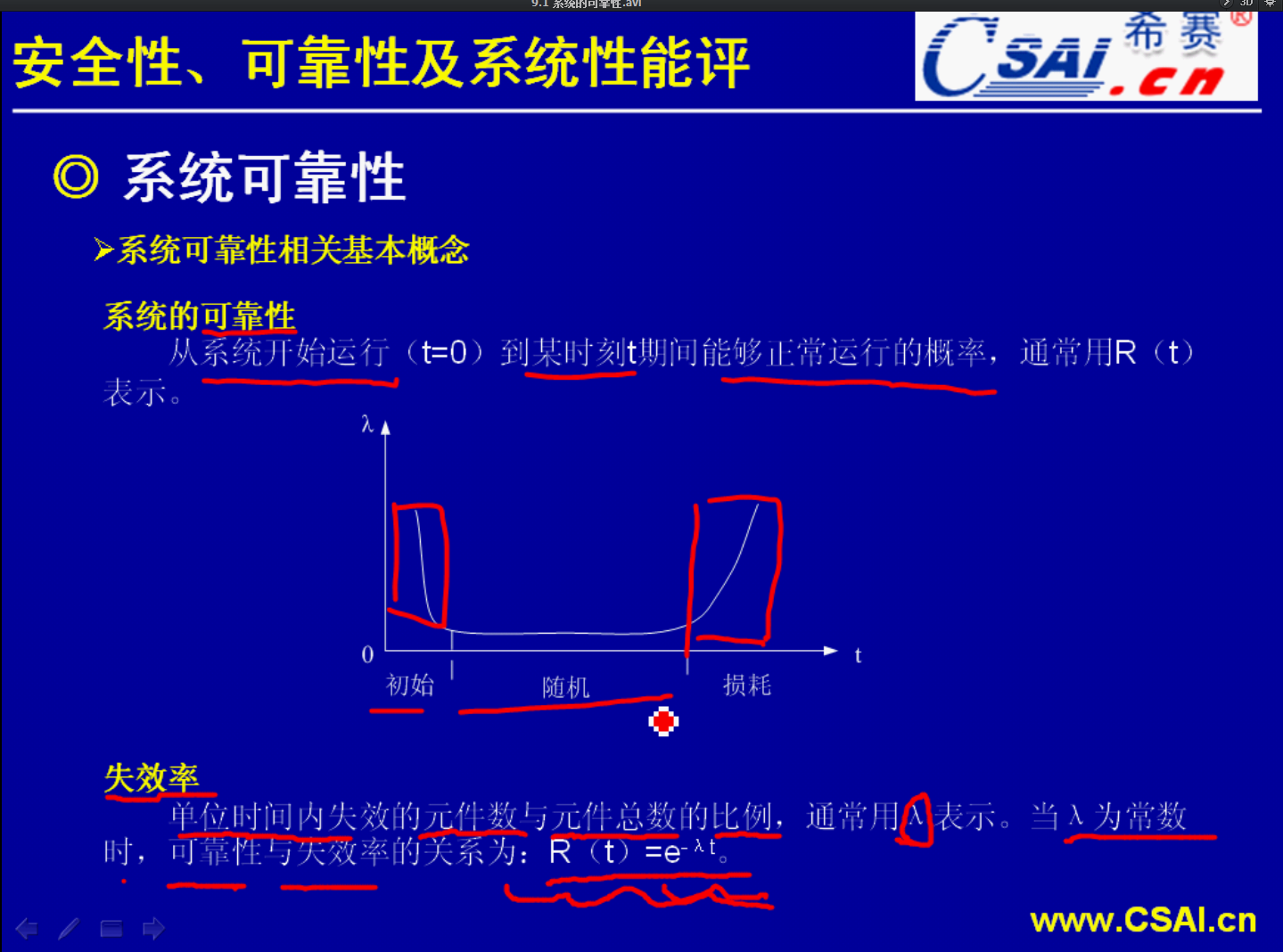
另外一个概念:平均无故障时间(MTBF).这一个概念在软考当中也出现过几次了.也就是第一次发生故障到第二次发生故障它们之间的一个时间间隔的平均值,就称为平均无故障时间.
平均修复时间(MTRF).
像这种公式必须是要记住的.这个λ呢就是我们刚才所说的失效率.1/λ就得到了平均无故障时间.
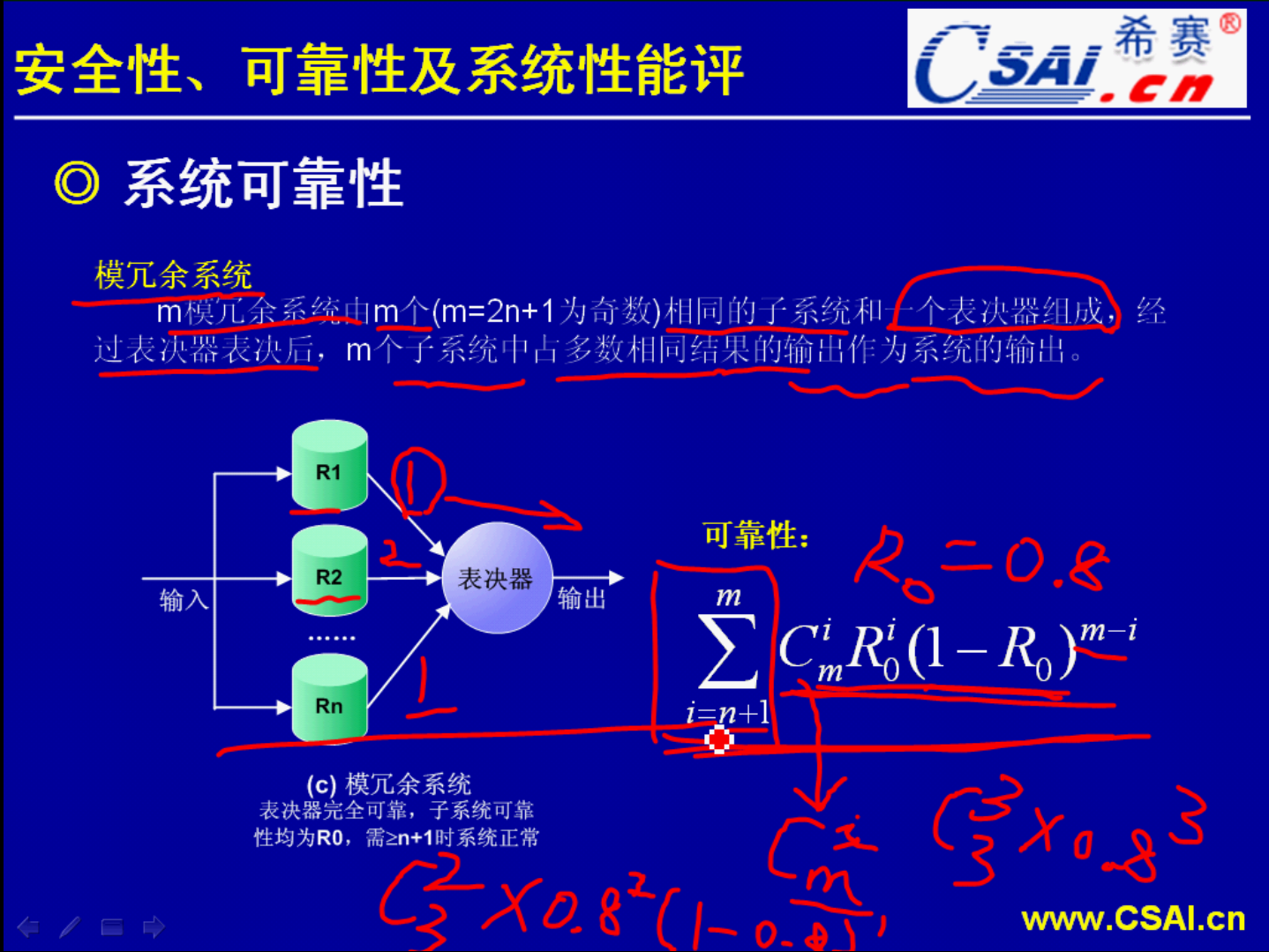
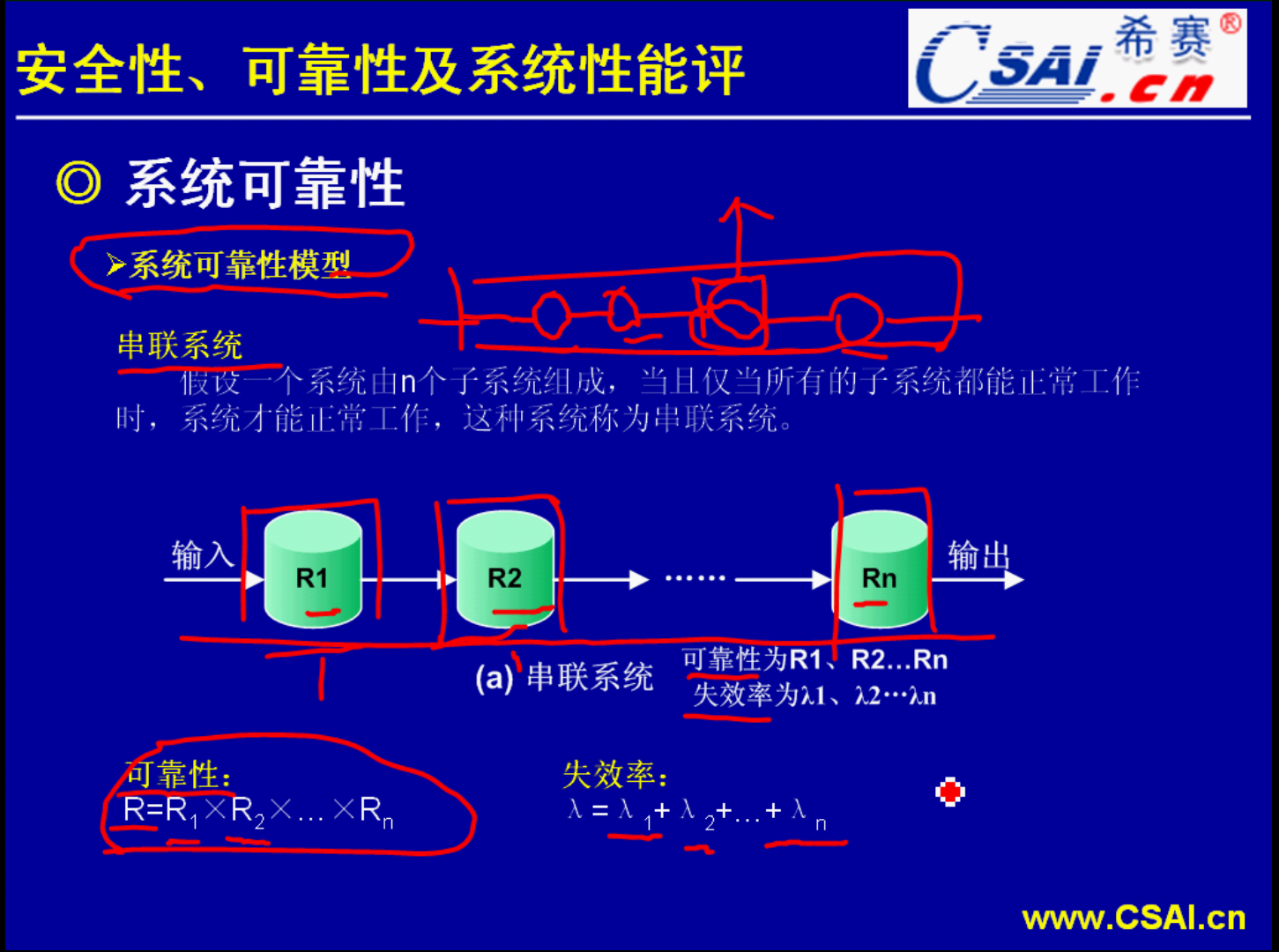
系统可靠性模型是我们这一部分知识的一个重点.主要就是因为它考察的比较多,在这一部分我们主要要来学习串联系统、并联系统和冗余系统的可靠性分析.
既然是串联而成,只要中间有一个结点出了问题,那么就会影响到整个系统的正确率,一个可靠性的问题.
R1、R2、....Rn都是子系统.这种系统的失效率和可靠性如何计算呢?知道子系统的失效率和可靠性如何计算整体的失效率和可靠性?我们有公式来计算.
所以系统的可靠性比任何一个子系统它的可靠性都要低.这是串联系统.由于它的可靠性降低,失效率就在提升.可靠性和失效率是一个反关系.可靠性高的话失效率也就低,失效率高可靠性也就低.失效率的计算是把每一个子系统的失效率相加.
例题:软考试题,是一个真题.
串联系统整体的系统可靠性比任何一个子系统它的可靠性都要低.而并联系统总的系统它的可靠性比子系统都要高.对于公式一定要记忆好掌握好.
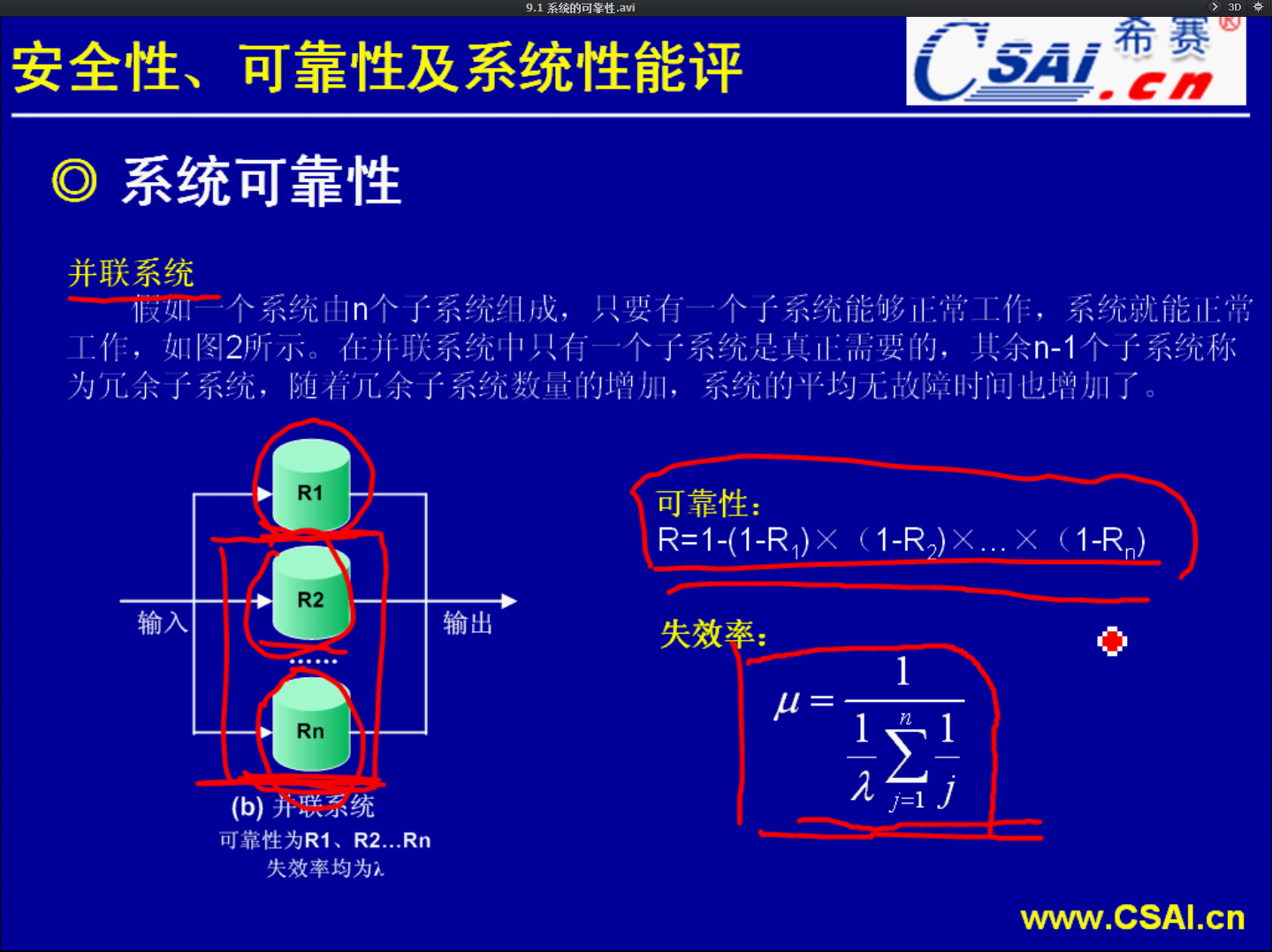
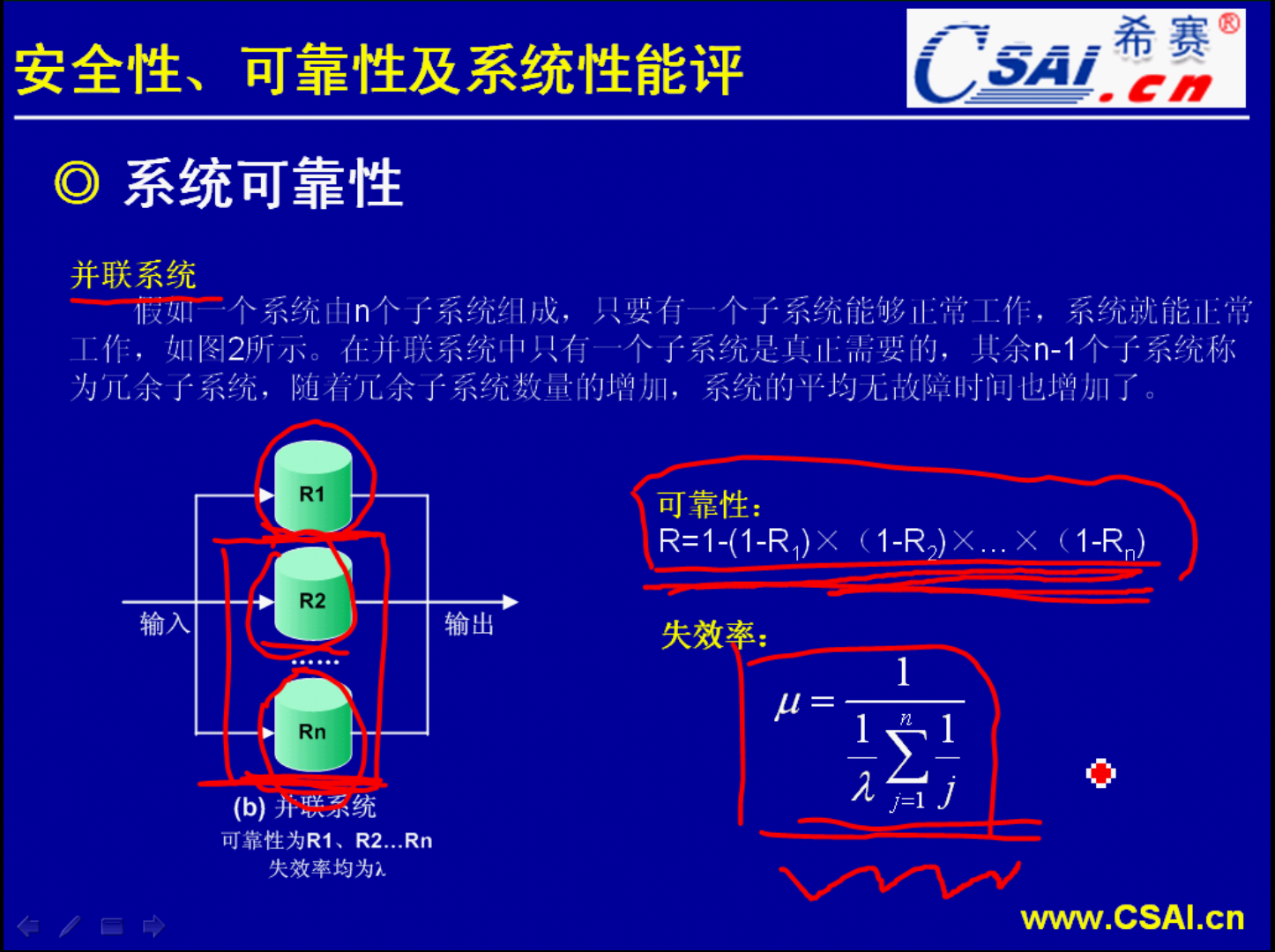
串联系统和并联系统,我们都假定子系统它会出正确结果.我们都假定这个子系统不会发生冲突.因为可能出现这种状况,在并联的这种系统中,
但是实际上它是有可能出错的.就我们刚才所说的情况,第一个计算出来的结果1,第二个计算出来的结果2,
公式里面的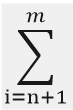
是指的对后面这个式子中的i取值从n+1到m,把这些式子分别取值然后相加起来.这个
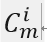它的意思就是组合数,它是一个组合数,就是从m中选i个元素出来有多少种选择.那么这一个公式也是要求大家记忆的.
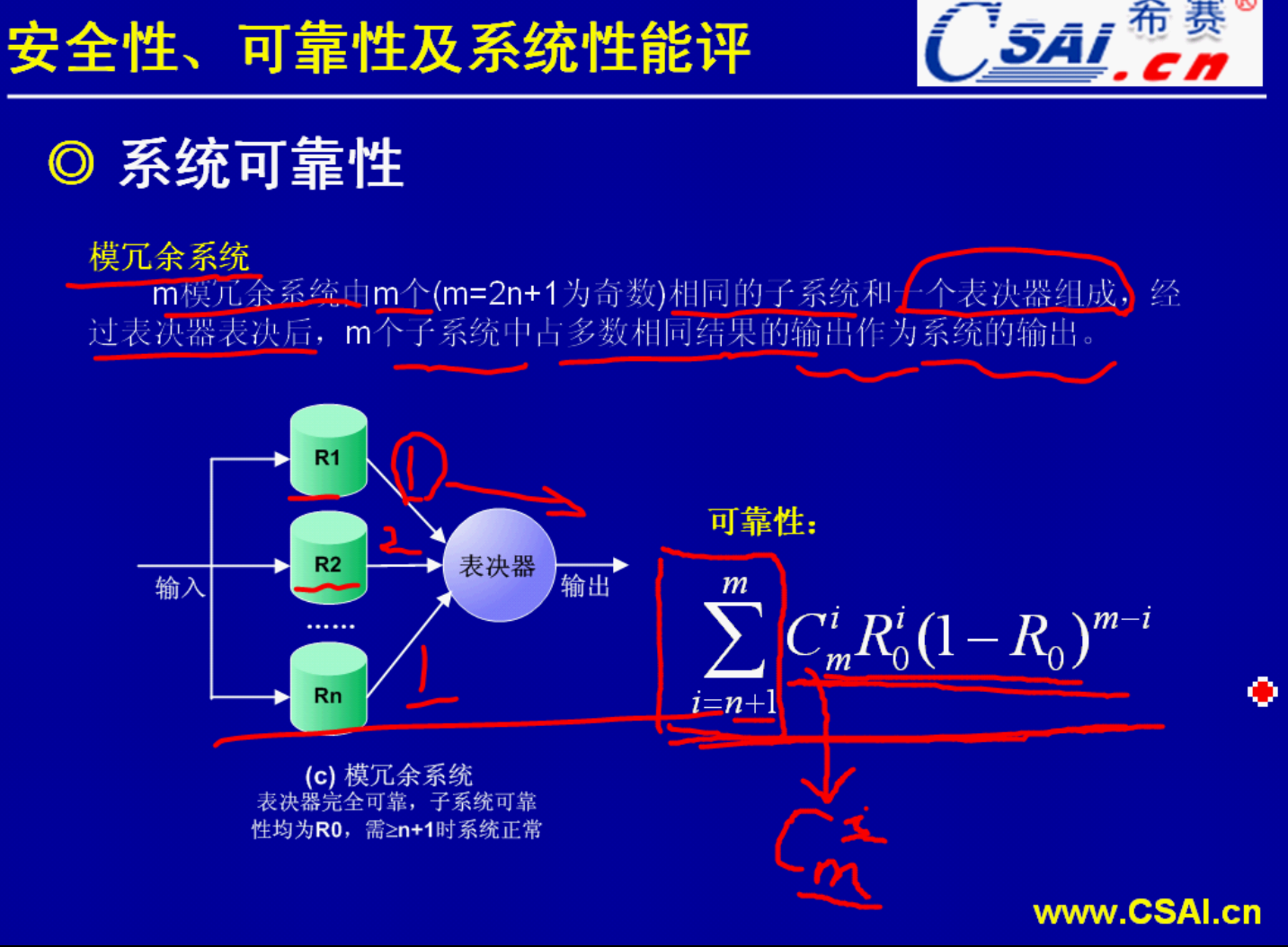
那么我们现在就来看一个例题.这里有一个表决模型,它的要求是?如果有一个运算结果两个子系统运算出来的结果是相同的,那么输出的结果就是这一个结果.那么这个系统当中的子系统它们的可靠性为0.8时,要求计算整个系统的一个可靠性,那么我们就要套用这一个公式了.由于子系统它的可靠性为0.8,所以我们的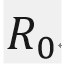
是等于0.8,由于我们的总的子系统的个数是3,而3个中间需要两个它才能算是正确答案.要有两个计算出来的结果是正确的,也就是有这两个不失效才能够得到正确的一个结果,总的这个系统它才不会失效.所以这里的n应该是1.所以我们就套用这一个公式来进行求解.也就是(
=
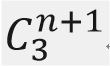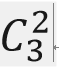)*0.8^2*(1-.0.8)^1,这个也就是我们的第一项,因为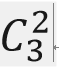=3,接下来i增加1,就变成了
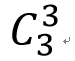*0.8^3*(1-0.8)^0.这一项呢就是我们的第二项.公式就是这么来套用的.用同样的方法我们可以求得当单个子系统它的可靠性为0.5的时候,
这就是系统可靠性,对于冗余表决模型它的一个计算.所以这几个公式要求大家一定要掌握、一定要记忆好.
