152.图论

图论是近年来发展迅速而又应用广泛的一门新兴学科。它最早起源于一些数学游戏的难题研究。如1736年欧拉（L . Euler)所解决的哥尼斯堡七桥问题；以及在民间广为流传的一些游戏问题：例如迷宫问题、棋盘上马的行走路线问题等等。   这些古老的问题当时吸引了许多学者的注意，从而在这些问题研究的基础上，又提出了著名的四色猜想和环游世界各国的问题。   图论不断发展，它在解决运筹学，网络理论，信息论，控制论，博奕论以及计算机科学等各个领域的问题时，显示出越来越大的效果。   对于这样一门应用广泛的学科，其包含的内容是丰富的，本篇我们只准备介绍基本的概念和定理，为今后有关学科及课程的学习和研究提供方便。

1.图

 1.1定义

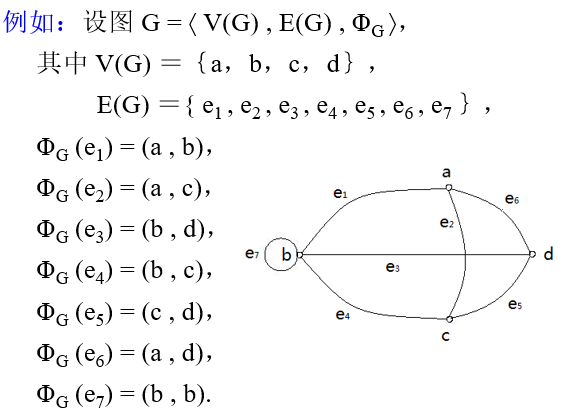
定义：一个图 G 是一个三元组< V(G) , E(G) , Φ_G >
       其中 V(G) 是非空的结点（顶点）集合，

　　E(G) 是边的集合，

　　Φ_G 是从边集 E 到结点偶对集合上的函数。

讨论定义：
(1) V(G) ={ v1 , v2 , … , vn }是非空的结点集合，vi 称为结点，简称V是点集。

(2) E(G)={e1 , … , em}为边的集合，ei 称为边，简称 E 为边集。

(3) Φ_G 是从边集 E 到结点偶对集合上的函数。即对于每条边 ei ，都存在V中的结点偶对与之相对应。

　　例如       Φ_G (ei) = (vi , vj)

(4) 定义中的结点偶对可以是有序偶对 <vi , vj> ，也可以是无序偶对 (vi , vj) 。

　　①若边 e 对应有序偶对 <vi , vj> ，则称边 e 是有向边（弧），

    　　 结点 vi 称为有向边的起点，结点 vj 称为有向边的终点，统称为 e 的端点。

　　　  也称 e 是关联于结点vi 和 vj 的，结点vi 和 vj 是邻接的（相邻的）。

　　②若边 e 对应无序偶对 (vi , vj)，则称边 e 是无向边（棱）。

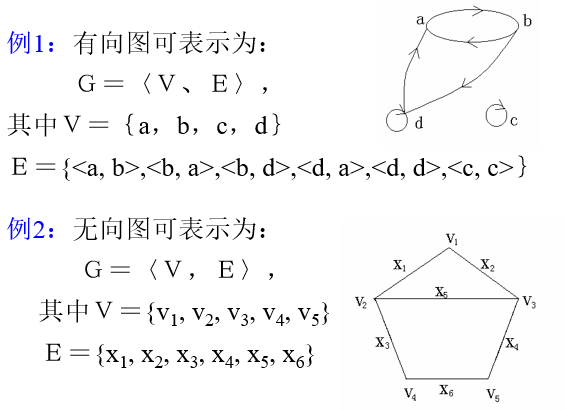
(5) 每条边都是有向边的图，称为有向图；
　  每条边都是无向边的图，称为无向图。
(6) 若令 e＝ <vi , vj> 或 e＝ (vi , vj)，即以结点偶对来表示图的边，这样可把图简化成：
      Ｇ＝<Ｖ,Ｅ >.

 

专有名词：

(1) ( n , m) 图：具有 n 个结点，m 条边的图。

(2)有向完全图：在 n 个结点的有向图
　　G = <V , E> 中，如果 E＝V×V，则称G为有向完全图。

 例如

 

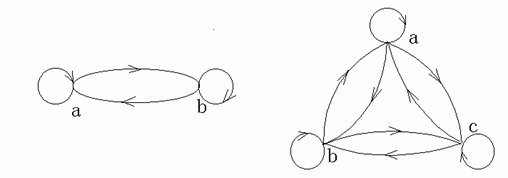
注：对于有向简单完全图：其有向边条数 m＝ 2 C_n² ＝ n(n-1)  （除去自回路）

(3)无向完全图：每两个结点之间均有连线的无向图。
    具有 n 个结点的无向完全图的边数为：m＝ C_n² ＝ n(n-1)/2

例如

(4)混合图：既有有向边，又有无向边的图。
(5)互相邻接的边：连接于同一结点的二条（或若干条）边。

 例如

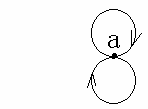
(6) 自回路：图中起始且终止于同一结点的边。
(自回路的箭头方向是没有意义的 )

(7)多重边（平行边）：二个结点之间方向相同的二条（多条）边。

 例如

 

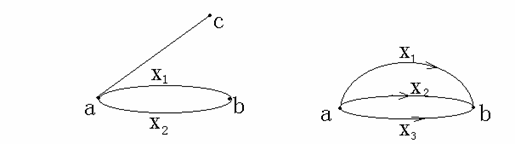
（8）含有多重边的图称为多重图，非多重图称为线图。

  例如

 

(9) 简单图：无自回路的线图称为简单图。
　　             即简单图是没有自回路和多重边的图。

(10) 赋权图Ｇ是一个三元组〈V , E , g〉或四元组〈V , E , f , g 〉，
其中 V 为结点集合，E 为边的集合，f 是定义在集合 V上的函数，g 是定义在集合 E 上的函数。

实际上，赋权图可以用一句话概括：每一条边或结点均注上数字的图（数字可以为整数、正实数）

 

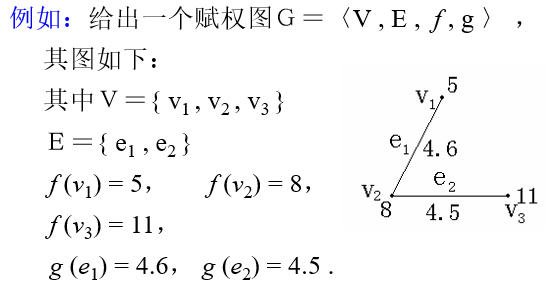
(11)孤立结点：不与任何结点相连接的结点。
(12)零图：仅包含孤立结点的图，记为 ( n , 0 ).
(13)平凡图：只有一个结点的图（1 , 0）.

1.2节点的次数

1.2.1定义

在有向图 G 中，对于任何结点 v，
①以 v 为始点的边的条数，称为结点 v 的引出次数（出度），记作 deg⁺(v) ；
②以 v 点为终点的边的条数称为 v 的引入次数（入度），记作 deg^-(v) ；
③结点 v 的引入次数和引出次数之和称为结点 v 的次数（度数），记作 deg(v)，即
deg(v) = deg⁺(v) + deg^-(v) .

对于无向图：

结点 v 的度数等于与该结点 v 相关联的边的条数，也记为 deg(v) 。

正则图：所有结点的度数均相同的简单无向图。

例如

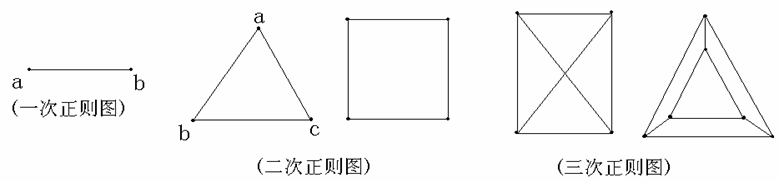
 1.2.2定理

定理1

设 G 是一个 (n , m) 图，它的结点集合为 V ={ v1 , v2 , … , vn } ，则

即所有结点度数的总和等于边数的两倍。

推论：

在任何图中，
(1) 所有结点的度数之和必为偶数；
(2) 度数为奇数的结点必有偶数个。

定理2

在任何有向图中，所有结点的入度之和等于所有结点的出度之和。

1.3路与回路

1.3.1路径

定义：

在一个图中，从结点 v0 到结点 vn 的一条路径 P 是：图的一个点边交替序列
（ v0 e1 v1 e2 v2 … en vn ）。
即从结点 v0 出发经过某些结点，而最终到达终点 vn 的点边交替序列称为图的路径。

讨论定义：
⑴ 从一个结点到某一结点的路径（若有的话），不一定是唯一的；

例如：设有向图Ｇ，求起始于１，终止于３的路径。

 

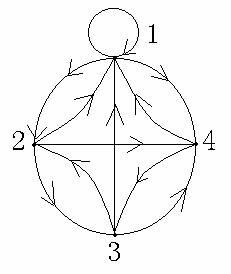
专有名词：

(1)穿程全部结点的路径：经过图中所有结点的路径。
(2)简单路径：在某一路径中，如果同一条边仅出现一次的路径。
(3)基本路径：在某一路径中，如果同一顶点仅出现一次的路径。

(4)回路：如果某路径的起点 v0 和终点vn 相重合，则称此路径为回路。
(5)简单回路：通过每条边不超过一次的回路。
(6)基本回路：通过每个结点不超过一次的回路。
(7)非回路图：没有任何回路的简单有向图。

讨论：

①回路不包含自回路。
②不是基本路径的任何路径都会包含回路，而去掉这些回路就可以得到基本路径。

1.3.2路径的表示方法

(a)边的序列表示法：设G = <V , E> 为一有向图，vi ∈ V ，则路径可以表示成：
      (< v1 , v2 > , < v2 , v3 > , … , < vk-1 , vk >)
(b)结点表示法： 在非多重图中，也可用顶点序列 (v1 , v2 , … , vk ) 表示路径。

1.3.3路径长度

 若两个结点之间有一条路经Ｐ，则路径 P 的长度|Ｐ|＝Ｐ中边的条数。

1.4图的性质

1.4.1可达性

定义： 

设图Ｇ为简单有向图，且 vi , vj V，若从 vi 到 vj 存在任何一条路径的话，则称 vi 到 vj 是可达的

 注：

可达性一定满足：自反性；可传递性

定义：

 从 vi 到 vj 的最短路径的长度称为距离，并记作： d<vi , vj> 

讨论定义：
(1) d<vi , vi> = 0
(2) d<vi , vj> ≥ 0
(3) d<vi , vj> + d<vj , vk> ≥ d<vi , vk>
(4)规定：若 vi 到 vj 是不可达的，则d<vi , vj> = ∞.
(5) 在有向图中，若 vi 到 vj 是可达的，且 vj 到 vi 也是可达的，
     但 d<vi,vj> 不一定等于 d<vj, vi>。

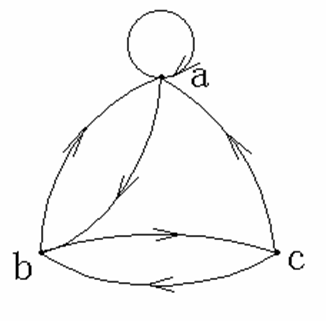
例如

d< c, a > = 1,
d< a, c > = 2

 

1.4.2联通性

定义：

 对于无向图 G，如果任何两个结点是相互可达的，则称图G是连通的

 对于有向图来讲，如果两结点均是互相可达的，则称此图是强连通的

 若图中任何结点偶对中至少有一点到另一结点是可达的，则称此图是单侧连通的

 对于简单有向图的伴随无向图（底图），若是连通的，则称此图为弱连通的

注：伴随无向图即为去掉箭头方向的图。

 定理：

一个有向图是强连通的充要条件是它包含一个回路，且该回路至少包含每个结点一次

定义：

设G = <V , E>为一简单有向图，且Ｇ’是Ｇ的子图。

对于某一性质而言，若没有其他包含Ｇ’的子图具有这种性质，

则称子图Ｇ’是相对于该性质的极大子图。

具有强连通性质的极大子图Ｇ’称为强分图；
具有单侧连通性质的极大子图Ｇ’称为单侧分图；
具有弱连通性质的极大子图Ｇ’称为弱分图。

定理：

在任一简单有向图Ｇ＝＜Ｖ，Ｅ＞中，有向图的每一个结点恰好处于一个强分图之中。

1.5图的矩阵表示

矩阵是研究图的有关性质的最有效的工具，可运用图的矩阵运算求出图的路径、回路和其它一些性质

1.5.1图的邻接矩阵表示

定义：

设G = <V , E>是简单有向图，其中V={v1, v2, … , vn}。定义一个 nn 的矩阵 A，并把其中各元素 aij 表示成：

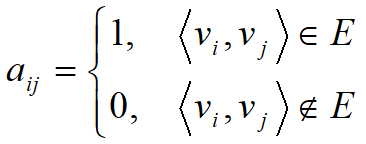
则称矩阵 A 为图 G 的邻接矩阵。

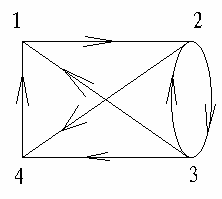
例如：设图 G = <V , E>
如图所示

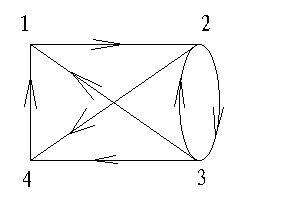
则图 G 的邻接矩阵为

 

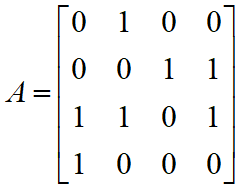
讨论定义：

⑴ 图G的邻接矩阵中的元素为0和1，
∴又称为布尔矩阵；

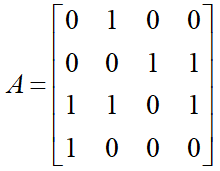
⑵ 图G的邻接矩阵中的元素的次序是无关紧要的，

只要做 行和行、列和列的交换，则可得到相同的矩阵。

∴若有二个简单有向图，则可得到二个对应的邻接矩阵，

若对某一矩阵做行和行、列和列之间的交换后得到和另一矩阵相同的矩阵，则此二图同构。

⑶ 当有向图中的有向边表示关系时，邻接矩阵就是关系矩阵；
⑷ 零图的邻接矩阵称为零矩阵，即矩阵中的所有元素均为0；

⑸ 在图的邻接矩阵中，
①行中1的个数就是行中相应结点的引出次数（出度）.
②列中1的个数就是列中相应结点的引入次数（入度）.

1.5.2 矩阵的计算

设有向图 G = <V , E>的邻接矩阵为 A，

则G的逆图 = <V , > 的邻接矩阵就是 A^T。

 

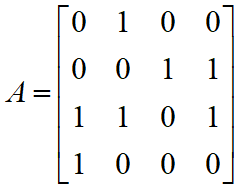
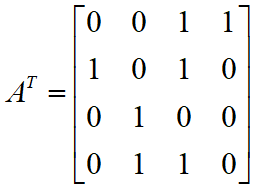
1.5.2.1AA^T 的元素的意义

设有向图 G = <V , E> 的邻接矩阵为 A，并令 B = AA^T，则

 

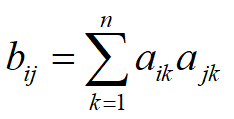
分析：元素 a_ik = 1 意味着存在边<vi , vk> .
　　元素 a_jk = 1 意味着存在边<vj , vk> .

结论：如果从结点 vi 和 vj 两者引出的边，能共同终止于某些结点 vk ，则这些终止结点 vk 的数目就是 bij 的值，

　　特别地，当 i = j 时，元素 b_ii 的值就是结点 vi 的引出次数。

 

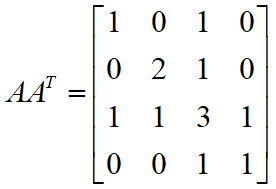
主对角线上的数，表示结点 i 的引出次数。

1.5.2.2A^TA 的元素的意义

设有向图 G = <V , E> 的邻接矩阵为 A，并令 B = A^TA，则

 

分析：元素 aki = 1 意味着存在边<vk , vi> .
　　元素 akj = 1 意味着存在边<vk , vj> .

结论：如果从某些结点 vk引出的边，能同时终止于结点 vi 和 vj ，则这些起始结点 vk 的数目就是 bij 的值，

　　特别地，当 i = j 时，元素 b_ii 的值就是结点 vi 的引入次数。

 

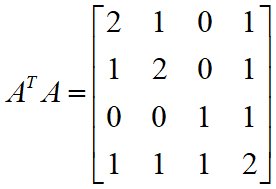
主对角线上的数，表示结点 i 的引入次数

 1.5.2.3A⁽ⁿ⁾ 的元素的意义

 设有向图 G = <V , E> 的邻接矩阵为  A = ( a_ij )，则 A⁽²⁾ 的元素

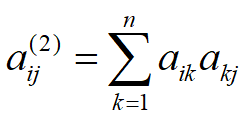
分析：元素 aik = 1 意味着存在边<vi , vk> .
　　元素 akj = 1 意味着存在边<vk , vj> .

所以，元素 a_ij⁽²⁾ 的值表示从结点 vi 到 vj 存在长度为 2 的不同路径的条数。

结论： A⁽ⁿ⁾ 的元素 a_ij⁽ⁿ⁾ 的值表示从结点 vi 到 vj 存在长度为 n 的不同路径的条数。
特别，对角线上的元素 a_ii⁽ⁿ⁾ 表示经过结点 vi的长度为 n 的不同回路的条数。

 例如

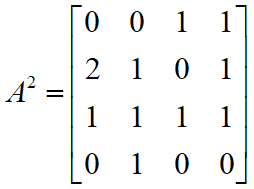A² 表示 i 和 j 之间具有长度为2的路径数

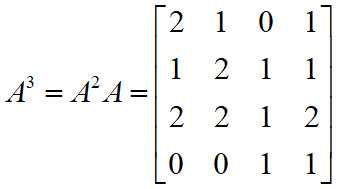A³ 表示 i 和 j 之间具有长度为3的路径数

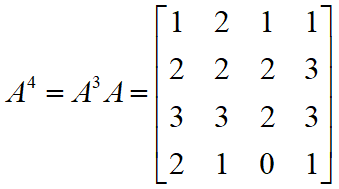A⁴ 表示 i 和 j 之间具有长度为4的路径数

1.5.2.4可达性矩阵

 

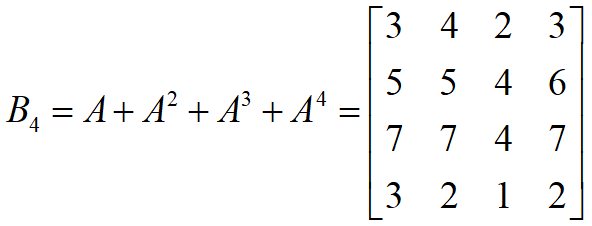
注：bij 表示从结点 vi 到 vj 有长度分别为 1，2，3，4 的不同路径总数。
此时， bij ≠ 0，表示从 vi 到 vj 是可达的。
bij = 0，表示从 vi 到 vj 是不可达的。因此， bij 表明了结点间的可达性。

 定义：

设 G = <V , E> 是简单有向图，其中 |V|=ｎ（ n  I+），定义一个 nn 矩阵 P，它的元素为：

则P称为图G的可达性矩阵。

注：由矩阵 B_n 可计算出可达性矩阵 P，其方法是：若 B_n中（i , j）元是非“0”元素，则令对应的 p_ij = 1，否则令 p_ij = 0 。

 例如：若

 

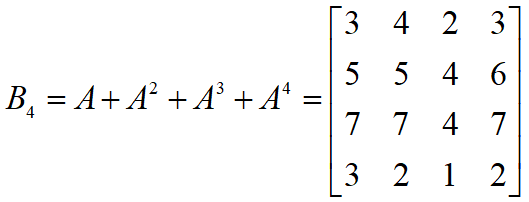
则

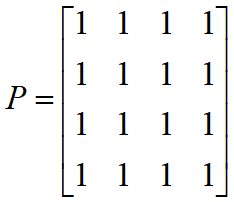
1.5.2.5可完全关联矩阵

 定义：

设无向图G = <V , E> ，
V = {v1 , v2 , … , vn}， E = {e1 , e2 , … , em}，
令 B = ( bij )_n×m，其中

 

则称B为无向图G的完全关联矩阵

讨论定义：

⑴ 完全关联矩阵为布尔矩阵；
⑵ 对应B中行均为0的结点为孤立结点，只有一个“1”的行的结点一定为悬挂的边，且一定不在任一回路中；
⑶ 全部为1的行的结点必定联结图中所有的结点。

例如

 

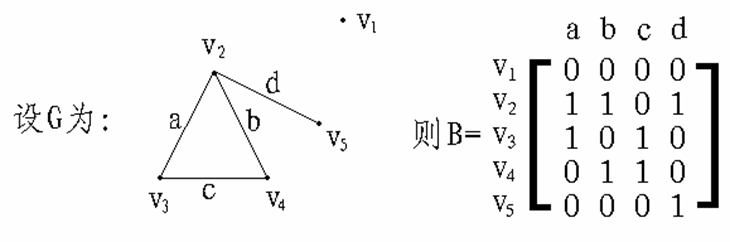
1.6特殊图

1.6.1欧拉图

定义：

欧拉路径：穿程于图 G 的每条边一次且仅一次的路径。
欧拉回路：穿程于图 G 的每条边一次且仅一次的回路。
欧拉图：具有欧拉回路的图。

定理：

 无向连通图 G 具有一条欧拉路径，当且仅当 G 具有零个或两个奇数度数的结点。

推论：

无向连通图 G 具有一条欧拉回路（欧拉图），当且仅当图G 所有结点度数全为偶数。

例如：用定理解决哥尼斯堡桥的问题

 

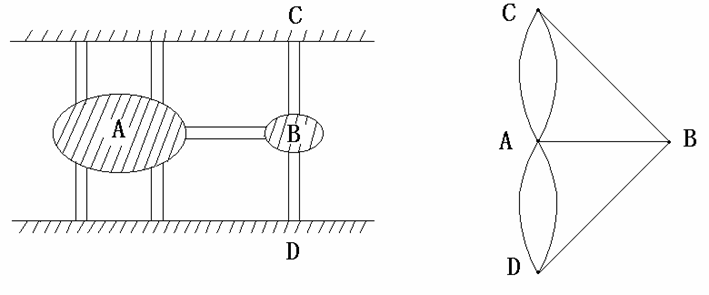
定理：

有向连通图 G 具有欧拉回路，当且仅当 G中每一个结点的引入次数等于引出次数，即Deg⁺(v)＝ Deg^-(v) .

 定理：

有向连通图 G 具有欧拉路径，当且仅当除了二个结点（其中一个的引入次数比引出次数大１，

另一个的引入次数比引出次数小１）以外的所有结点的引入次数等于引出次数，即Deg⁺(v)＝ Deg^-(v) .

 1.6.2 哈密尔顿图

定义

哈密尔顿路径：穿程于无向图 G 的每一个结点一次且仅一次的路径。
哈密尔顿回路：穿程于无向图 G 的每一个结点一次且仅一次的回路。
哈密尔顿图：具有哈密尔顿回路的图。

到目前为止，还没有找到哈密尔顿路径存在的充分必要条件。下面介绍两个定理。

定理：

设 G = < V , E > 是具有n 个结点的简单无向图，若在 G 中每一对结点次数之和大于或等于(n-1)，

则在 G 中一定存在一条哈密尔顿路径。

 注：此定理是充分条件，而不是充分必要条件

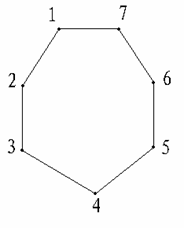
例如：ｎ＝７，G = <V , E > 见图：每对结点次数为４<７－１＝６，但确有一条汉密尔顿路径。

 

定理:

若图 G = < V , E > 是哈密尔顿图，则对于结点集 V 的每个非空真子集 S 均有
W( G ―S ) ≤ |S| 成立，
其中 W(G－S) 表示从G中删除S后，所得图的连通分图个数； |S| 表示 S 中的结点数。

2.树与生成树

2.1无向树（树）

2.1.1定义

连通的且无简单回路的无向图称为无向树，简称树

 

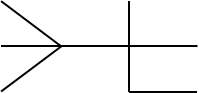
专用名词：
树叶(终点)：树中度数为1的结点。
分枝点(内点)：树中度数大于1的结点。
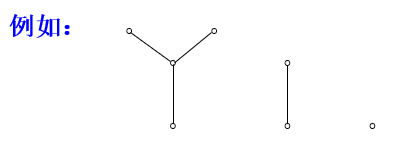
森林：每个连通分图均为树的无向图。

2.1.2树的性质

设T是一棵树，vi，vj 为T中两个不同的结点，则：
1) vi 和 vj 仅有一条路径相连通。
2) 在T中加一条边{ vi , vj }，则由此而形成 的图，仅有一个回路。

在一棵(n , e)树中有e=n-1。(n表示结点数，e表示边数)

设F是由 t 棵树组成的(n , e)森林，则有e=n-t。

在结点大于2的(n , e)树中，所有结点的度数之和为2(n-1)

在任一(n ≥ 2)的树T中，至少有二片树叶。

2.2生成树

2.2.1定义

一个无向图G的生成子图是树TG，则称TG是G的生成树(支撑树)。

讨论定义：

1) G的生成树不是唯一的。

2)如何在连通图G中寻找一棵生成树：

①若G没有循环，则G本身就是一棵树；

②若G仅有一条循环，从此循环中删去一条边，仍保持图的连通性，得到一棵生成树。

③若G有多条循环，则逐个对每条循环重复②中操作，直到打断G中所有循环，得到一棵生成树为止。

定理：

任何连通无向图至少有一棵生成树

给定一个连通图，寻找其生成树的数目是图论中树的计数问题

含 n （n>1）个结点的标记完全图K_n 有 n^n-2 棵标记生成树

定义：

生成树T中的边称为树枝，不在生成树T中但属于图G的边，称为树T的弦，弦的集合称为树T的补。

在一个连通赋权图中，树枝的权之和为最小的生成树称为最小生成树。

Kruskal算法：

设G有n个结点，m条边，先将G中所有边按权的大小次序进行排列，不妨设：

W(e1) < W(e2) < … < W(e_m)，

①k←1，A←Ø。

②若AU{ek}导出的子图中不包含简单循环，则A ← A U{ek}

③若A中已有n-1条边，则算法终止，否则K← K+1，转至②。

这一算法假设G中权均不相同，对于边权任意情况也完全适用。这时求得的最小生成树不唯一

2.3有向树与根树

定义：

若有向图在不考虑边的方向时是一棵树，称之为有向树。

定义：

一棵有向树，如果恰有一个结点的入度为0，其余所有结点的入度都为1，则称为根树。入度为0的结点称为根，出度为0的结点称为叶，出度不为0的结点称为分枝点或内点。任何结点的级(高度)是从根出发到该结点的路径长度(边的条数)。

定义：

指明了根树中结点或边的次序的树为有序树。在有序树中，如每个结点有明确级，同一级的结点排在同一行，并明确它们位置，则这样的树称位置树

定义：

在根树中，若每一个结点的出度小于或等于m，则称这棵树为m叉树。若每个结点的出度恰好等于m或零，则称这棵树为完全m叉树，若其所有树叶层次相同，称为正则m叉树。

特别，当m=2时，称为二叉树。

很多实际问题可用二叉树或m叉树表示。任何一棵有序树都可以把它改写为一棵对应的二叉树。

定义：

在有向树T中，由结点V和它的所有子孙所构成的结点子集V’以及从V出发的所有有向路中的边所构成的边集E’组成T的子图

方法：

设有序树T中结点Vi 的r棵子树有根Vi1, Vi2 , …, Vir，其顺序自左向右，则在二叉树T’中Vi1是Vi 的左儿子，Vi2是Vi1的右儿子，Vi3是Vi2的右儿子….，Vir是Vir－1的右儿子。