AOJ 0121 Seven Puzzle

                                                 7 パズル

7 パズルは 8 つの正方形のカードとこれらのカードがぴたりと収まる枠で構成されています。それぞれのカードには、互いに区別できるように 0, 1, 2, ..., 7 と番号がつけられています。枠には、縦に 2 個、横に 4 個のカードを並べることができます。

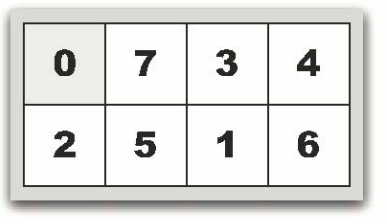
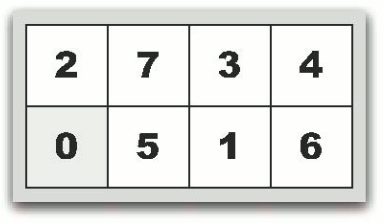
7 パズルを始めるときには、まず枠にすべてのカードを入れます。枠のなかで 0 のカードだけは、上下左右に隣接するカードと位置を交換することができます。たとえば、枠の状態が図(a) のときに、0 のカードの右に隣接した、7 のカードと位置を交換すれば、図(b) の状態になります。あるいは、図(a) の状態から 0 のカードの下に隣接した 2 のカードと位置を交換すれば図(c) の状態になります。図(a) の状態で 0 のカードと上下左右に隣接するカードは 7 と 2 のカードだけなので、これ以外の位置の入れ替えは許されません。

ゲームの目的は、カードをきれいに整列して図(d) の状態にすることです。最初の状態を入力とし、カードをきれいに整列するまでに、必要な最小手数を出力するプログラムを作成してください。ただし、入力されたカードの状態からは図(d) の状態に移ることは可能であるとします。

入力データは、1 行に 8 つの数字が空白区切りで与えられます。これらは、最初の状態のカードの並びを表します。例えば、図(a) の数字表現は0 7 3 4 2 5 1 6 に、図(c) は 2 7 3 4 0 5 1 6 となります。

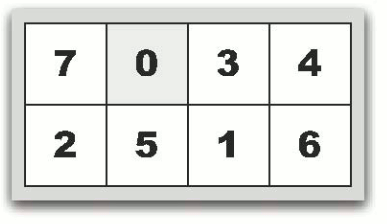図(a) 0 7 3 4 2 5 1 6 の場合	図(b) 7 0 3 4 2 5 1 6 の場合

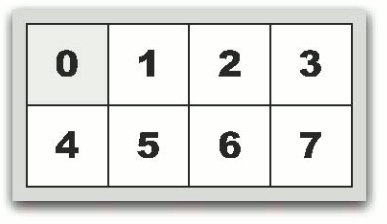図(c) 2 7 3 4 0 5 1 6 の場合	図(d) 0 1 2 3 4 5 6 7 (最終状態)

Input

上記形式で複数のパズルが与えられます。入力の最後まで処理してください。 与えられるパズルの数は 1,000 以下です。

Output

各パズルについて、最終状態へ移行する最小手数を１行に出力してください。

Sample Input

0 1 2 3 4 5 6 7
1 0 2 3 4 5 6 7
7 6 5 4 3 2 1 0

Output for the Sample Input

1
28
题意：在2*4的方框里随意填充了0到7共八个数字，每一个点位的数字都可以和相邻点位的数字交换位置，通过这样的交换，最终要使得8个数字(0,1,2...7)顺序的从左往右从上到下依次排列，
即排列成  0 1 2 3
         4 5 6 7
思路：深度优先搜索，不断交换某一个元素的位置，可以穷尽所有的情况，不妨不断交换0元素的位置，从01234567这种最特殊的情况开始交换(这种情况交换次数为0)，之后0每换一次位置后产生一种新的情况，理所应当的这种情况需要交换的次数为0未交换时情况所需交换次数再加1.以此类推……获得所有情况所需交换次数即可。
代码：

#include<iostream>
#include<map>
#include<string>
#include<algorithm>
#include<queue>
using namespace std;
map<string, int>dp;//容器里存放每一种情况
int direction[4] = { 1,-1,4,-4 };
void bfs() {
    queue<string>que;
    que.push("01234567");
    dp["01234567"] = 0;
    while (!que.empty()) {
        string s = que.front();que.pop();
        int index;
        for (int i = 0;i < 8;i++) 
            if (s[i] == '0') { index = i; break; }
        for (int i = 0;i < 4;i++) {
            int x = index + direction[i];
            if (x >= 0 && x <= 7 && !(index == 3 && i == 0) && !(index == 4 && i == 1)) {
                string next=s;
                swap(next[x], next[index]);
                if (dp.find(next) == dp.end()) {//说明容器里没有该元素
                    dp[next]=dp[s]+1;
                    que.push(next);
                }
            }
        }

    }
}
int main() {
    bfs();//找到所有情况的答案
    string s;
    while (getline(cin,s)) {
        s.erase(remove(s.begin(), s.end(), ' '), s.end());
        cout << dp[s] << endl;
    }
    return 0;
}