支配树学习笔记

@(学习笔记)[支配树]

简介

什么是支配树？支配树是什么？XD
对于一张有向图(可以有环)我们规定一个起点(r), 从(r)点到图上另一个点w可能存在很多条路径(下面将r到w简写为(r o w)).
如果对于(r o w)的任意一条路径中都存在一个点(p), 那么我们称点(p)为(w)的支配点(也可以称作是(r o w)的必经点), 注意(r)点不讨论支配点. 下面用idom[u]表示离点u最近的支配点.
对于原图上除(r)外每一个点(u), 从(idom[u])向(u)建一条边, 最后我们可以得到一个以(r)为根的树. 这个树我们就叫它"支配树".

联想

这个东西看上去有点眼熟?
支配点和割点(删掉后图联通块数增加)有什么区别?
我们考虑问题给定一个起点(r)和一个终点(t), 询问删掉哪个点能够使(r)无法到达t.
很显然, 我们删掉任意一个(r o t)的必经点就能使(r)无法到达(t), 删掉任意一个非必经点, (r)仍可到达(t).
从支配树的角度来说, 我们只需删掉支配树上(r)到(t)路径上的任意一点即可
从割点的角度来说, 我们是不是只需要考虑所有割点, 判断哪些割点在(r o t)的路径上即可？是否将某个割点删掉即可让(r)无法到达(t)?
这当然是不正确的, 我们可以从两个方面来说明它的错误：

1. 删掉割点不一定使(r)无法到达(t)
    
   这个图中点(u)是关键点(删掉后图联通块个数增加)
   并且(u)在(r o t)的路径上, 然而删掉点(u)后(r)仍然可以到达(t)
2. 图中不一定存在割点
    
   在这个图中不存在任何割点
   所以我们没有办法使用割点来解决这个问题.

简化问题

1. 树
   对于一棵树, 我们用r表示根节点, u表示树上的某个非根节点. 很容易发现从(r o u)路径上的所有点都是支配点, 而(idom[u])就是(u)的父节点.
   这个可以在(O(n))的时间内实现.
2. DAG(有向无环图)
   因为是有向无环图, 所以我们可以按照拓扑序构建支配树.
   假设当前我们构造到拓扑序中第(x)个节点编号为(u), 那么拓扑序中第(1) ~ (X - 1)个节点已经处理好了, 考虑所有能够直接到达点(u)的节点, 对于这些节点我们求出它们在支配树上的最近公共祖先(v), 这个点(v)就是点(u)在支配树上的父亲.
   如果使用倍增求LCA, 这个问题可以在(O((n+m)log n))的时间内实现.

对于这两个问题我们能够很简便的求出支配树.

有向图

对于一个有向图, 我们应该怎么办呢？
简单方法:
我们可以考虑每次删掉一个点, 判断哪些点无法从r到达.
假设删掉点(u)后点(v)无法到达, 那么点u就是(r o v)的必经点(点(u)就是(v)的支配点).
这个方法我们可以非常简单的在(O(nm))的时间内实现.
其中(n)是点数, (m)是点数.
更快的方法:
这里, 我将介绍Lengauer-Tarjan算法.
这个算法能在很短的时间内求出支配树.

关于这个算法的具体证明, 推荐一下两篇博客:
http://www.cnblogs.com/meowww/p/6475952.html
https://ssplaysecond.blogspot.jp/2017/03/blog-post_19.html

本篇博客主要讲解的是Lenguaer-Tarjan算法的实现.

首先来介绍一些这个算法的大概步骤:

1. 对图进行DFS(深度优先遍历)并求出搜索树和DFS序. 这里我们用dfn[x]表示
   点(x)在DFS序中的位置.
2. 根据半必经点定理计算出一个点的半必经点, 作为计算必经点的依据
3. 根据必经点定理修正我们的半必经点, 求出支配点

半必经点

我们用idom[x]表示点x的最近支配点, 用semi[x]表示点x的半必经点.
那什么是半必经点呢?
对于一个节点(Y), 存在某个点(X)能够通过一系列点(p_i)(不包含(X)和(Y))到达点(Y)且(forall p_i)都有(dfn[p_i]>dfn[Y]), 我们就称(X)是(Y)的半必经点, 记做(semi[Y]=X)
当然一个点(X)的"半必经点"会有多个, 而且这些半必经点一定是搜索树中点(X)的祖先(具体原因这里不做详细解释, 请自行思考).
对于每个点, 我们只需要保存其半必经点中dfn最小的一个, 下文中用semi[x]表示点x的半必经点中dfn值最小的点的编号.
我们可以更书面一点的描述这个定理：

1. 对于一个节点(Y)考虑所有能够到达它的节点, 设其中一个为(X). 若(dfn[X]<dfn[Y]), 则(X)是(Y)的一个半必经点
    
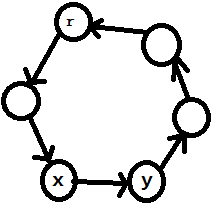
2. 若(dfn[X]>dfn[Y]), 那么对于(X)在搜索树中的祖先(Z)(包括(X)), 如果满足(dfn[Z]>dfn[Y])那么(semi[Z])也是Y的半必经点
    

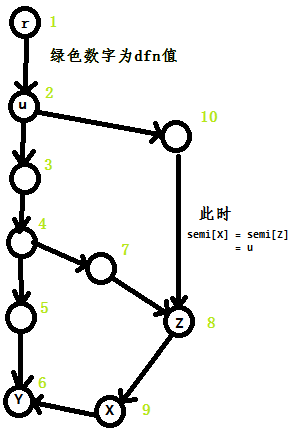
在这些必经点中, 我们仅需要dfn值最小的
这个半必经点有什么意义呢?
我们求出深搜树后, 考虑原图中所有非树边(即不在树上的边), 我们将这些边删掉, 加入一些新的边 ({ (semi[w],w) : w∈V 且 w e r }), 我们会发现构建出的新图中每一个点的支配点是不变的, 通过这样的改造我们使得原图变成了DAG
是否接下来使用DAG的做法来处理就可以做到(O((n + m) log n))呢？我没试过, 不过还有更好的方法.

必经点

一个点的半必经点有可能是一个点的支配点, 也有可能不是. 我们需要使用必经点定理对这个半必经点进行修正, 最后得到支配点.
对于一个点(X), 我们考虑搜索树上(semi[X])到(X)路径上的所有点(p_0, p_1 ... p_k). 对于所有(p_i: 0 < i < k), 我们找出(dfn[semi[p_i]])最小的一个(p_i)记为(Z)
考虑搜索树上(X)与(semi[X])之间的其他节点(即不包含(X)和(semi[X])), 其中半必经点dfn值最小的记为(Z)
如果(semi[Z]=semi[X]), 则(idom[X]=semi[X])

如果(semi[Z] e semi[X]), 则(idom[X] = idom[Z])

具体实现

为了方便实现, semi[i]在代码中的含义与讲解中有所出入. 它表示的是一个点的半支配点的dfn值.
对于求半必经点与必经点我们都需要处理一个问题, 就是对于一个节点(X)的前驱(Y), 我们需要计算(Y)在搜索树上所有dfn值大于(dfn[X])的祖先中semi值最小的一个, 我们可以按dfn从大到小的顺序处理, 使用带权并查集维护, 记录每一个点到并查集的根节点的路径上semi值最小的点, 这样处理到节点(X)值时所有dfn值比(X)大的点都被维护起来了.
这样我们就能够在(O((n+m) cdot alpha(n)))时间内解决这个问题.
放一下代码吧:

#include<cstring>
#include<vector>
#include<algorithm>
#include<deque>

using namespace std;

const int N = 1 << 17, M = 1 << 19;

struct graph
{
	int head[N], top;
	vector<int> pre[N];
	
	struct edge
	{
		int v, nxt, w;
	}edg[M << 1];
	
	inline void init()
	{
		memset(head, -1, sizeof(head));
		top = 0;
		
		for(int i = 0; i < N; ++ i)
			pre[i].clear();
	}
	
	inline void addEdge(int u, int v)
	{
		edg[top].v = v, edg[top].nxt = head[u];
		head[u] = top ++;
		pre[v].push_back(u);
	}
	
	int dfn[N], idx[N], clk;
	vector<int> bck[N]; //bck[i]记录以i为半支配点的节点的集合, 以方便计算idm[].
	int idm[N], sdm[N];
	int preOnTree[N];
	
	struct disjointSet
	{
		int pre[N], w[N];
		
		void access(int u, int *sdm)
		{
			if(pre[u] == u)
				return;
			
			access(pre[u] , sdm);
			
			if(sdm[w[pre[u]]] < sdm[w[u]])
				w[u] = w[pre[u]];
			
			pre[u] = pre[pre[u]];
		}
	}st;
	
	void dfs(int u)
	{
		dfn[u] = clk;
		idx[clk ++] = u;
		
		for(int i = head[u]; ~ i; i = edg[i].nxt)
			if(! (~ dfn[edg[i].v]))
				preOnTree[edg[i].v] = u, dfs(edg[i].v);
	}
	
	inline void tarjan(int s)
	{
		memset(dfn, -1, sizeof(dfn));
		clk = 0;
		
		for(int i = 0; i < N; ++ i)
			bck[i].clear();
		
		for(int i = 0; i < N; ++ i)
			st.pre[i] = st.w[i] = i;
			
		preOnTree[s] = -1;
		dfs(s);
		
		for(int i = 0; i < N; ++ i)
			idm[i] = i, sdm[i] = dfn[i];
		
		for(int i = clk - 1; ~ i; -- i)
		{
			int u = idx[i];
			
			for(vector<int>::iterator p = bck[u].begin(); p != bck[u].end(); ++ p)
			{
				int v = *p;
				st.access(v, sdm);
				idm[v] = sdm[st.w[v]] == sdm[v] ? u : st.w[v];
			}
			
			bck[u].clear();
			
			if(! i)
			{
				idm[idx[i]] = sdm[idx[i]] = -1;
				break;
			}
			
			for(vector<int>::iterator p = pre[u].begin(); p != pre[u].end(); ++ p)
				if(~ dfn[*p]) //考虑到原图可能不联通
				{
					int v = *p;
					st.access(v, sdm);
					sdm[u] = min(sdm[u], sdm[st.w[v]]);
				}
			
			bck[idx[sdm[u]]].push_back(u);
			st.pre[u] = preOnTree[u];
		}
		
		for(int i = 1; i < clk; ++ i)
			idm[idx[i]] = idm[idx[i]] == idx[sdm[idx[i]]] ? idm[idx[i]] : idm[idm[idx[i]]];
	}
};