1.树状数组
现阶段,树状数组主要用于维护序列前缀和 (其实还支持区间和、区间异或和、区间乘积和RMQ等具有交换律的问题) 。
长这样: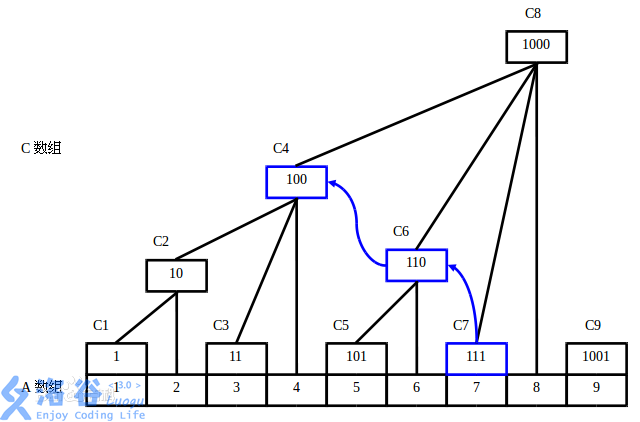
树状数组看似复杂的构造,其实都是以一个思想为基础:
将(i)二进制分解,最小的二的次幂记为lowbit(i)
结合差分思想,做到区间修改,单点查询。洛谷P3368
*树状数组求逆序对(二维偏序)洛谷P1908 洛谷P1774:
//定义数组,b[]为读入的数组,a[]为要离散化后的数组,c[]为树状数组
struct node
{int v,id;}a[N];
bool cmp(const node &x,const node &y)
{return x.v<y.v;}
int main()
{
scanf("%lld",&n);
for(int i=1;i<=n;i++)
scanf("%lld",&a[i].v),a[i].id=i;
sort(a+1,a+n+1,cmp);//按价值从大到小排序
int cnt=1;
for(int i=1;i<=n;i++)//离散化+去重
{
if(i!=1 &&a[i].v!=a[i-1].v)cnt++;
b[a[i].id]=cnt;
}
for(int i=1;i<=n;i++)
update(b[i],1),ans=ans+i-sum(b[i]);//因为是排完序之后,所以之前加入的一定比后加入的大
//然后在查询当前这个数前面位置的数,就是逆序对的个数了
printf("%lld
",ans);
return 0;
}
总结:
时间复杂度:(O(nlogn))(上限) 空间复杂度:(O(n))
树状数组以其代码量少,思想简洁著称,可以单独使用,也可以和其他数据结构结合,达到锦上添花的效果。不足之处呢,就是能维护的的东西局限较大,难以单独实现其他算法。
练习:洛谷P1774(结合冒泡排序思想就变成逆序对裸题)
*洛谷P3810(三位偏序,要用到CDQ分治) 还没弄懂
2.线段树
线段树之所以称为“树”,是因为其具有树的结构特性。线段树由于本身是专门用来处理区间问题的(包括RMQ、RSQ问题等。)
大概长这样:
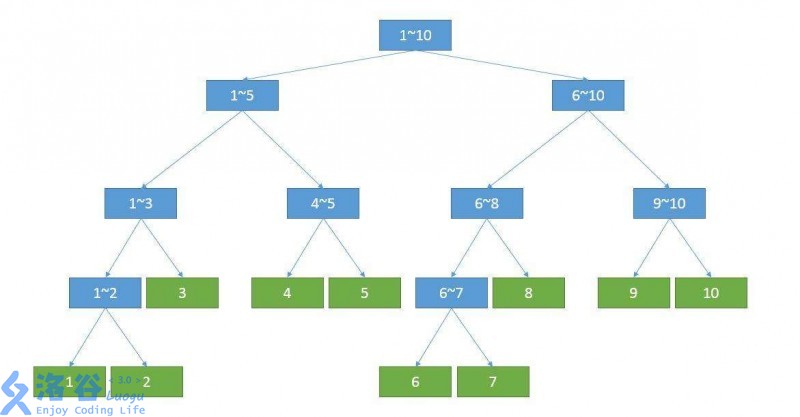
几点基础性质:
1.线段树每个节点都是一个区间
2.对于每一个区间为([l,r])非叶节点(k),它的左儿子是(k<<1),区间为([l,mid]),右儿子是(k<<1|1),区间为([mid+1,r])。其中(mid=(l+r)>>1)
下面以维护区间和,支持区间修改的线段树为例,实现它的各种操作。
关于区间修改操作:
延迟标记(Lazy tag)
详细地说,我们在执行修改命令时,可以先不对所有子节点立刻修改,而是在受影响的父节点上标记,表示“该节点已被修改,但其子节点尚未更新”。这样在询问向下递归时,就可以顺便计算父节点标记(修改)对它的影响。
我们以add数组代表标记数组,每次如果查询子节点就将标记下传:
void pushdown(int k,int l,int r)//标记下传
{
if(add[k]==0) return;
int mid=(l+r)>>1;
Add(k<<1,l,mid,add[k]);
Add(k<<1|1,mid+1,r,add[k]);
add[k]=0;
}
*标记一个以上,记得考虑运算优先级!洛谷P3373
其他的题目也差不多,分析好维护的是什么,怎么修改,怎么设置标记,怎么下传。注意细节,线段树的初级应用还是不难的。
例题:
洛谷P2574(维护xor) 洛谷SP7259双倍经验的紫题
总结:
时间复杂度:(O(nlogn)) 空间复杂度:(O(4n)^+)
线段树可扩展的空间很大,但是我还没学到那么多,在此就不多赘述了。总而言之,线段树真的是一个非常强的数据结构,在区间维护问题上几乎是万能的存在。我还是慢慢研究吧。
3.散列表(Hash)
与离散化类似的是,Hash能把若干复杂的信息映射到一个容易维护的值域内,从而降低统计难度。哈希的过程,其实可以看作对一个串的单向加密过程,并且需要保证所加的密不能高概率重复。
Hash算法应用较广泛,我只学习了 字符串哈希。
直接上例题理解吧:洛谷P3370
给定N个字符串(第i个字符串长度为Mi,字符串内包含数字、大小写字母,大小写敏感),请求出N个字符串中共有多少个不同的字符串。
对于100%的数据:N<=10000,Mi≈1000。
进制哈希:
给出出一个固定进制base,将一个串的每一个元素看做一个进制位上的数字,所以这个串就可以看做一个base进制的数,那么这个数就是这个串的哈希值;则我们通过比对每个串的的哈希值,即可判断两个串是否相同。
long long hashe(char s[])
{
int len=strlen(s);
long long ans=0;
for (int i=0;i<len;i++)
ans=(ans*base+s[i])%mod+prime; //核心操作,可类比十进制。
//+prime可增加hash的可行度(不加本题可能会被卡哦)
return ans; //mod 最好取一个较大的质数,作用同上。
}
如果字符串较多,难免出现Hash值一样的字符串,这种现象叫做哈希碰撞。
怎么解决?
1、无错哈希:挂链表之类的操作。
2、多重哈希:就是字面意思
总结:
Hash表与其说是一种数据结构,不如说是一种sao操作算法。它对于复杂信息的统计有着很大的应用。但是考试时其实Hash的应用不算特别多(我反正基本没用过),而且哈希函数的选择也比较玄学,因此这里就不详细讲了。