大意
给定一个 (w), 找到所有的 (x),使得 (x) 的约数和等于 (w)。
题解
感觉好久没做过数学题了(本来就没做过几道),突然感觉自己跟废了一样,正好算着考试题把以前的东西捡一捡...
这道题用到的数学知识不多,就是算数基本定理跟约数和定理,下面简单说一下:
算数基本定理(唯一分解定理)
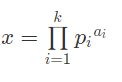
也可以写成
[N={p_1}^{c_1} imes {p_1}^{c_2} imes ... imes {p_m}^{c_m}
]
约数和定理
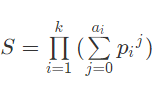
也就是
[Sum(N)=(p_1^0+p_1^1+...+p_1^{c_1}) imes (p_2^0+p_2^1+..+p_2^{c_2}) imes ... imes (p_n^0+p_n^1+..+p_n^{a_n})
]
至于证明请自行百度...
分析
再剩下的就是暴力搜索了吧...其实跑的很快的说。
我们既然已经知道了 (w),那么任务是找到 (x) ,对于 (x) 有 (x={p_1}^{c_1} imes {p_1}^{c_2} imes ... imes {p_m}^{c_m}) ,也就是说 (w=(p_1^0+p_1^1+...+p_1^{c_1}) imes (p_2^0+p_2^1+..+p_2^{c_2}) imes ... imes (p_n^0+p_n^1+..+p_n^{a_n})) 。所以,我们枚举每个素数 (p_i) 和每个素数的指数 (0...c_i) 来对 (w) 进行分解,每用完一个素数,就令答案记录 (x) 乘上 ({p_i}^{k}) ((k) 不一定等于 (c_i),(k) 是我们当前枚举到的指数),如果某一时刻 (w) 被分解到了1,那么此时的 (x) 就是一个答案。
注释感觉还是打的挺详细的
#include <bits/stdc++.h>
using namespace std;
#define Game return
#define Over 0
const int maxn = 1e6 + 10;
long long prime[maxn], prime_cnt;
bool v[maxn];
void Prime(long long n){//素数筛,大家都会
for(int i = 2; i <= n; i++){
if(!v[i]) prime[++prime_cnt] = i;
for(int j = 1; j <= prime_cnt && i * prime[j] <= n; j++){
v[i * prime[j]] = 1;
if(i % prime[j] == 0) break;
}
}
}
bool Isprime(long long x){//快速判断一个数是不是素数
if(x == 1) return 0;
if(x <= 100000){
if(!v[x]) return 1;
else return 0;
}
for(int i = 1; prime[i] * prime[i] <= x; i++)
if(x % prime[i] == 0) return 0;
return 1;
}
long long a[maxn], cnt;//记录答案
void Dfs(int now, int p, int x){
//now为w分解到现在的值,p表示选到第p个素数,x为w已分解出来的若干个pi的ai次方连乘
//now = 1说明已经分解完毕
if(now == 1){
a[++cnt] = x;
return ;
}
//下面是判断一种特殊情况,如果now-1为素数,有(now-1)的0次方加上(now-1)的1次方得now
if(Isprime(now - 1) && (now - 1) >= prime[p])
a[++cnt] = x * (now - 1);
for(int i = p; prime[i] * prime[i] <= now; i++){
//进一步分解
long long pi = prime[i];//pi为prime[i]即第i个素数的若干次方
long long sum = prime[i] + 1;//sum为prime[i]的0次方+prime[i]的1次方+prime[i]的2次方...
while(sum <= now){
if(now % sum == 0) Dfs(now / sum, i + 1, x * pi);
pi *= prime[i];
sum += pi;
}
}
}
int main(){
long long w;
//根据算数基本定理,我们不必去找所有约数,可以直接用素数
//提高效率
Prime(100000);
//理论上只要筛到根号下2e9即可,但多筛点没什么影响
while(~scanf("%lld", &w)){
cnt = 0;
Dfs(w, 1, 1);
printf("%lld
", cnt);
sort(a + 1, a + 1 + cnt);
for(int i = 1; i <= cnt; i++)
printf("%lld ", a[i]);
if(cnt) printf("
");//这个地方很坑...如果不存在就只有一行0,不用再打空行了...
}
}