算法的笔记 -概念性初始

(Python)算法:

1.引入概念:

如果a+b+c=1000,且a^2+b^2=c^2(a,b,c为自然数),如何求出a,b,c的组合?

枚举法:

工作量太大,浪费时间

for a in range(0,1001):
    for b in range(0,1001):
        c = 1000-a-b
        if a**2+b**2=c**2:
            print('a,b,c:%d,%d,%d'%(a,b,c)
#T(n)=n*n*(1+max(1,0))=n^2*2=O(n^2)
#或者:
for a in range(0,1001):
     for b in range(0,1001):
           for c in range (0,1001):
                if a+b+c=1000 and a**2+b**2=c**2:
                  	print('a,b,c:%d,%d,%d'%(a,b,c)
#时间复杂度:T=1000*1000*1000*2
#T(n)=n**3*2
#T(n)=k* (n**a)函数的走势决定力量是n**a,而k是决定函数的陡峭,决定不了函数的走向
#渐进函数:T(n)=g(n)=n**a,g(n)大O表示法,忽略系数     

算法:

解决问题的思路或方法,计算机处理信息的的本质,因为计算机本质上就是一个算法莱高速计算机确切的步骤来执行一个指定的任务,一般的,当计算机处理信息时,会从输入设备或者数据的存储地址读取数据,把结果写入输出设备,或者是某个存储地址以供以后调用.

算法是一个独立的一种解决问题的方法和思想

实现的语言并不重要,重要的是思想

算法的五大特征:

• 输入:算法具体有0个或者多个输出
• 输出:算法至少有一个输出或者多个输出
• 有穷性:算法在有限步骤之后会自动结束而不会无限循环下去,并且每一步可以在接收的时间内完成
• 确定性:算法中的每一步都有确定的含义,不会出现二义性
• 可行性:算法的每一步都是可执行的,也就是说每一步都够执行有限的次数完成

算法的效率衡量:

执行时间反应算法效率不是绝对可信.

时间复杂度:

时间复杂度是同一个问题可用不同的算法解决,而一个算法的质量优劣将影响到算法至程序的效率.(执行基本运算数量,每行代码执行次数)

计算器科学中,算法的事假复杂度是一个函数,他定性的描述了该算法的运行时间,这是一个关于代表算法输入值的字符串的长度函数.时间复杂度常用于大O符号表述,不包括函数的低阶项和首项系数.使用这种方式时,时间复杂度可被成为渐进的,他考虑当输入值大小趋近无穷时的情况.

算法的复杂度:

• 时间复杂度:指执行算法所需要的计算工作量(基本操作)
• 空间复杂度:指执行这个算法所需要的内存空间。

大O记法:

用于描述函数渐进行为的数学符号。更确切地说，它是用另一个（通常更简单的）函数来描述一个函数数量级的渐近上界。在数学中，它一般用来刻画被截断的无穷级数尤其是渐近级数的剩余项；在计算机科学中，它在分析算法复杂性的方面非常有用。

最坏时间复杂度:

算法完成工作量最少需要多少基本操作,即最优时间复杂度.

算法完成工作量最多需要多少基本操作,即最坏时间复杂度.

算法完成工作量平均需要多少基本操作,即平均时间复杂度.

• 对于最优时间复杂度,其价值不大,没有提供什么有用信息,反应最理想的状态,无参考价值.
• 对于最坏时间复杂度,提供一种保证,表明算法在此程度上的基本操作中一定能完成工作.
• 对于平均时间复杂度,是对算法的一个全面评价,完整全面的反应这个算法的性质,另一方面,这种权衡没有保证,不是每个计算机都能在这个基本操作内完成,对于平均情况的计算,也会因为应用算法的实例分布可能并不均匀而难以计算.
• 因此,我们只关注算法的最坏情况,即最坏时间复杂度.

时间复杂度的几条基本计算规则:

1. 基本操作:即只有常数项,认为其时间复杂度O(1)
2. 顺序结构:时间复杂度按加法进行计算
3. 循环结构:时间复杂度是按乘法计算
4. 条件结构:时间复杂度取最大值
5. 判断一个算法的效率时,往往只需要关注操作数量的最高层次项,其次要项和常数项可以忽略.
6. 在没有特殊的说明时,我们所分析的算法时间复杂度都是最坏时间复杂度.

Python内置类型性能分析:

timeit模块:

timeit模块可以用来测试一小段python代码的执行速度.

• class timeit.Timer(stmt = 'pass',setup='pass',timer=<timer function>)
• Timer是测量小段代码执行速度的类
• stmt参数是要测试代码的语句,注意是字符串形式的类型,将函数名()直接放在引号里面传进来
• setup参数是运行代码时需要的设置
• setup参数是运行代码时需要的设置
• timer参数是一个定时器函数,与平台无关.
• timeit Timer.timeit(number = 1000000)

Timer类中的测试语句执行速度的对象方法.number参数是测试代码的测试次数,默认是1000000次.方法返回执行代码的平均耗时,一个float类型的秒数.

列表的操作测试:

import timeit 
#生成列表的四种方式:
#列表的加法生成新的列表
li1 = [1,2]
li2 = [3,4]
li = li2+li1


li = [i for i in range(10000)]#列表生成器


li = list(range(10000))#把可迭代对象直接生成列表

#空列表追加形式生成列表
li = []
for i in range(10000):
    li.append(i)

from timeit import Timer 

def test1():
    li = []
	for i in range(10000):
    	li.append(i)

def test2():
    li = []
    for i in range(10000):
        li +=[i]
        
def test3():
    li = [i for i in range(10000)]
    
def test4():
    li = list(range(10000))
    
def test5():
    li = []
    for i in range(10000):
        li.extend([i]) #列表或可迭代对象
        
 def test6():
    li = []
    for i in range(10000):
        li.insert(0,i)
        
        
#注意不能直接把函数名直接传进来,是一个字符串的形式
t1  = Timer('test1()','from __main__ import test1')
print('append',t1.timeit(number = 1000),'seconds')
t2 = Timer('test2()','from __main__ import test2')
print('+',t2.timeit(number = 1000),'seconds')  
t3 = Timer('test3()','from __main__ import test3')
print('列表生成器',t3.timeit(number = 1000),'seconds') 
t4 = Timer('test4()','from __main__ import test4')
print('可迭代对象直接生成列表',t4.timeit(number = 1000),'seconds') 
t5 = Timer('test5()', 'from __main__ import test5')
print('列表extend:', t5.timeit(number=1000), 'seconds')
t6 = Timer('test6()', 'from __main__ import test6')
print('列表insert:', t6.timeit(number=1000), 'seconds')


#由结果可以看出:可迭代对象生成新列表时间最短,其次是列表生成器的时间,再次就是加法生成新列表的时间,最后是追加形式的时间最长,insert要比append慢的太多,extend是对列表或者可迭代对象的插入

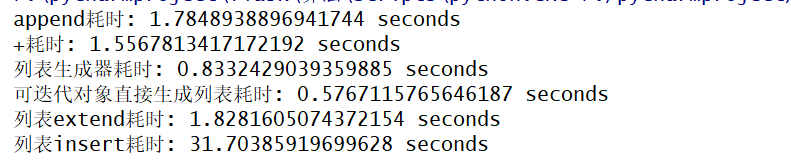
from timeit import Timer
x = list(range(2000000))

pop_zero = Timer('x.pop(0)','from __main__ import x')
print('pop_zero耗时:',pop_zero.timeit(number=1000),'seconds')


y = list(range(2000000))

pop_end = Timer('y.pop()','from __main__ import y')
print('pop_end耗时:',pop_end.timeit(number=1000),'seconds')

数据结构:

• DSA =Data Structure + Algorithm

• 度量:To measure is to know,if you can not measure it,you can not improve it

图灵机:

• tape:依次均匀地划分单元格,各注有某一字符,默认为'#'
• alphabet:字符的种类
• head:总是对准某一单元格,并可读取和改写其中的字符,经过一个节拍,可转左或者右的邻格
• state:TM总是处于有限种状态中的某一种,每经过一个节拍,可转向另一个状态.

Transition Function:(q,c;d,L/R,p)

• 若当前的状态为p且当前的字符是c,则将当前的字符改成d,转向左侧或者右侧的邻格,转入p状态.一旦进入特定的状态'h',则停机.

图灵机的实例:

• (<,1,0,L,<)----向左,1->0
• (<,0,1,R,>)---掉头,0->1
• (<,#,1,R,>)---
• (>,0,0,R,>)
• (>,#,#,L,h)

RAM模型:Random Access Machine

随机存取机器模型是算法分析与计算复杂度理论中的重要串行计算模型,简称为RAM.

一个RAM有:
	k个变址器/1,/2,/3,....,/k.
	无穷多个普通寄存器R0,R1,R2,...,
	和一个有穷长的程序组成.
#变址器也是寄存器,每个寄存器中可以存放一个自然数,但只有变址器的内容可以作为间接地址.
RAM的程序使用两种形式地址:
    1.直接地址:形式/j(j=1,2,...,k)或Ri(i=0,1,2...)
    2.间接地址:/j(j=1,2,3,...,k)
        3.如果/j中的存自然数为i,则/j代表地址Ri.
RAM的指令形式解读:
    1.A<-a,表示将地址A的内容改为自然数a.
    2.A<-B,表示将地址A的内容改为地址B的内容.
    3.A<-B*C,表示把地址B中的内容和地址C的内容作运算*之后,送入地址A中.
    4.A<-F(B<C),此时F是一个可以用多带图灵机器在多项式空间和对数多项式的巡回中实现的变换,A,B,C可以是直接地址也可以是间接地址,A为写入地址,B,C是读出地址.
    RAM除了可以用以上的指令编程序外,还可以判断某个寄存器或变址器的内容是否为0,实现条件转移.
    IF R[i] = 0 GOTO 1
    IF R[i] > 0 GOTO 1
    GOTO 1   (绝对转向)
    STOP     (终止语句)

算法分析:

自身的正确性和复杂度

复杂度:不必要真正的将算法的RAM的基本指令做统计累计的执行次数.

复杂度的方法:

• 迭代:级数求和
• 递归:递归跟踪+递推方案
• 猜测+验证

级数:

算术级数:与末项平方同阶
$$
T(n)=1+2+3+cdots+n=frac{n(n+1)}{2}=O(n^2)
$$

幂方级数:
$$
sum_{k=0}^{n}{kd}=int_{0}^{n}xddx=frac{1}{d+1}x^{d+1}|_{0}{n}=frac{1}{d+1}n^{d+1}=O(n{d+1})
$$

$$
T(n)=1²⁺²2+3^2+...+n2 = n(n+1)(2n+1)/6=O(n^3)
$$
收敛级数,调和级数,对数级数

实例:

取非极端元素

问题:给定整数子集S,|S|=n>=3,找出元素a 属于 S,a!=max(s)且a!=min(s)
算法:从s中任取三个元素{x,y,z}
//若s以数组形式给出,不妨取前三个
//由于S是集合,这三个元素必互异
确定排除最大最小者
//不妨设 x =max{x,y,z},y=min{x,y,z}
输出剩下的元素

#起泡排序
#问题:算法必然结束?至多迭代多少次
不变性:经过k轮扫描交换后,最大的元素必将就位
单调性:经过k轮交换后,问题的规模缩减至n-k.
正确性:经过至多n次扫描,算法必然会终止,且能给出正确答案
#封底估计:测量地球周长