首先明白什么是拓扑序列?
只有有向图才会有拓扑序列,每一条边的起点都在终点之前
例如:
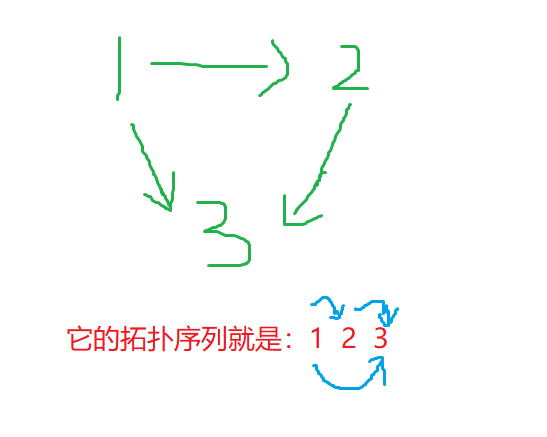
但如果是这样子的
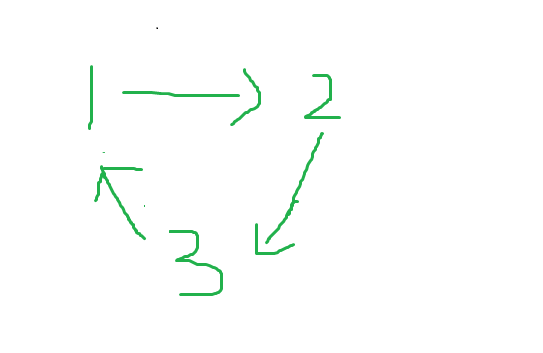
有向图中存在一个环 则它就不存在拓扑序列。
拓扑图:有向无环图一定存在拓扑序列,因此有向无环图也叫做拓扑图,所有入度为0的节点都可以作为起点,因此拓扑序列并不唯一。**
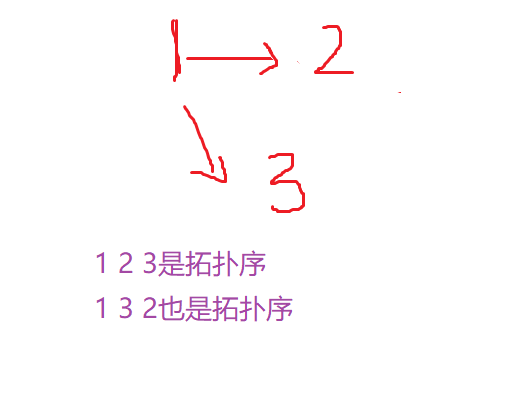
有向无环图一定存在拓扑序列是因为,一定至少存在一个入度为0的点,因此可以逐个突破,生成拓扑序,而一个环上的每个点入度必不为0。
生成拓扑序列的步骤
queue <- 所有入度为0的点
while queue不为空
{
t <- 取队头
枚举t所有出边 t-j
删掉t->j j入度减一:d[j]--
if(d[j] == 0) 说明节点j的入度为0 可以作为起点入队 queue <- j
所有点全部入队 拓扑序列排序完成
}
输出拓扑序(在队列中)
而且这个题体现出了用数组模拟queue的好处,用队列数组储存的正好是拓扑序
代码:
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 100010;
int n, m;
int h[N], e[N], ne[N], idx;
int q[N], d[N]; //d用来存一个点的入度
bool torsort()
{
int hh = 0, tt = 0;
for(int i = 1; i <= n; i++) //把入度数为0的节点全部入队
{
if(!d[i])
{
q[++tt] = i;
}
}
while(hh <= tt)
{
int t = q[hh++];
for(int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
d[j]--; //删出边
if(d[j] == 0) q[++tt] = j; //入队
}
}
return tt == n; //所有点都入队 则完成拓扑序
}
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
int main()
{
memset(h, -1, sizeof h);
scanf("%d%d", &n, &m);
for(int i = 0; i < m; i++)
{
int a, b;
scanf("%d%d", &a, &b);
add(a, b);
d[b]++; //入度加1
}
if(torsort())
{
for(int i = 1; i <= n; i++) printf("%d ", q[i]);
puts("");
}
else puts("-1");
system("pause");
return 0;
}