区间第k大问题用主席树解决,也即“可持久化线段树”。
前提条件:会线段树
比如给一个长度为7的数组,值分别是5,1,4,7,3,2,6让我们在里面维护区间第k大的值。首先想一下第k大我们怎么做,最朴素的方法是O(NlogN)排一下序然后输出a[k],但实际上我们可以O(N)用权值线段树解决。权值线段树是按照值域建的线段树(普通的线段树是按照index建的),其中每个结点存的d值是该值域区间里能在数组中取到的值的数量。(值域线段树不涉及tag,两个小区间合并也是严格的d值相加,所以其实比我们会的线段树要简单)这样的话我们在权值线段树树上询问第k大就是如果p->ls->d大于等于k,就在p->ls里找;否则在p->rs里找,k修改为k-p->ls->d。一直到询问到叶子节点为止。该数组建立权值线段树如下:
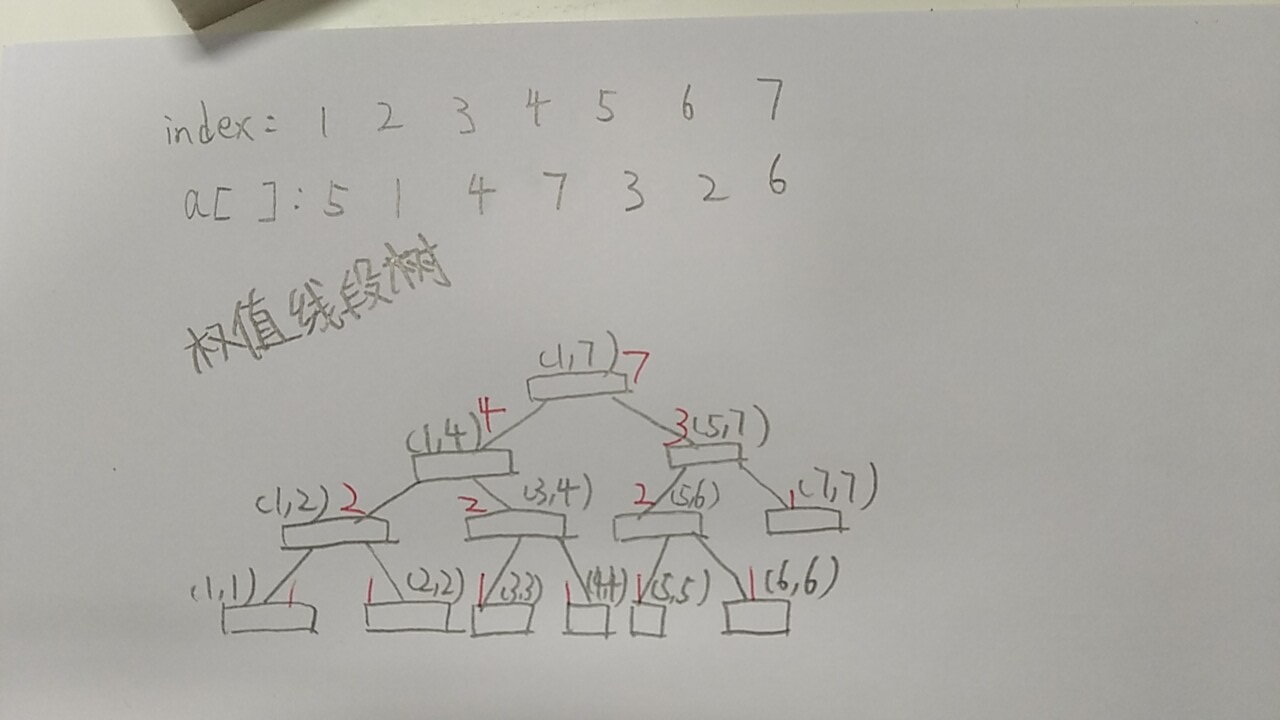
这里我们注意到(2,5)的线线树与(1,7)的线段树形状是一样的,形状一样是因为左值域右值域一样均为(min a[i],max a[i]),结点上的d值不一样因为区间不一样。

然后我们想到把所有的子区间都建一个权值线段树好了,长度为n的数组建出来n^2个权值线段树,询问哪个区间第k大就在哪个线段树里找就行。比如询问(2,5)的第k大,那我们建一个线段树然后在里面询问就好了。
但这样是不行的,因为每次建树时间复杂度O(N),建n^2个就是n^3复杂度,四舍五入就是一个亿啊!然后就迎来了主席树:我们建n个权值线段树,第i棵是按1~n建的权值线段树。
index: 1 2 3 4 5 6 7
a[]: 5 1 4 7 3 2 6
开始建:
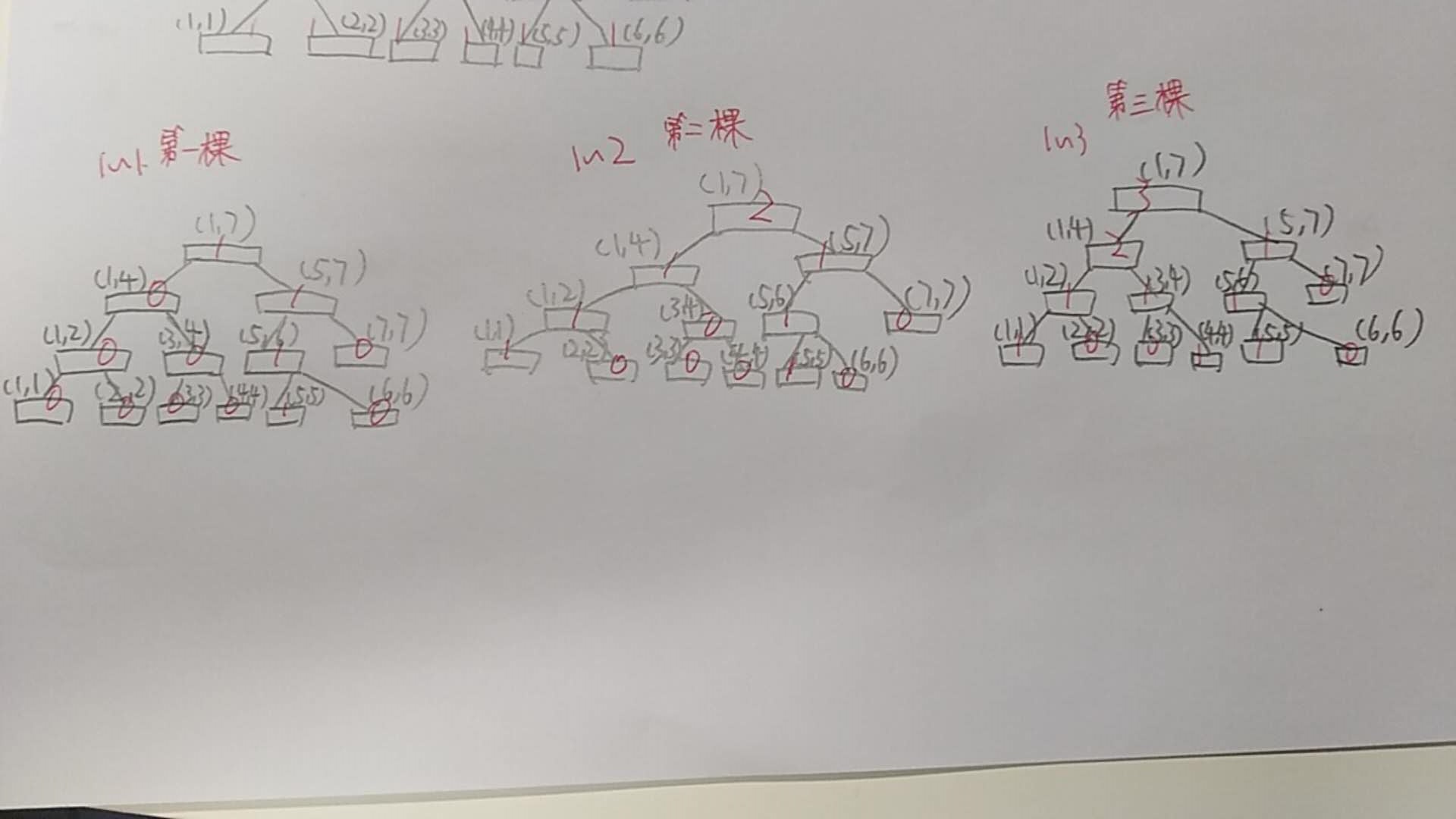
建着建着我们我们发现第i棵树可以由第i-1棵树插入a[i]得到,每次插入修改logN个结点,而不是全部,所以相同的信息被重复存储了。所以我们可以进行优化:
第一棵树照常建
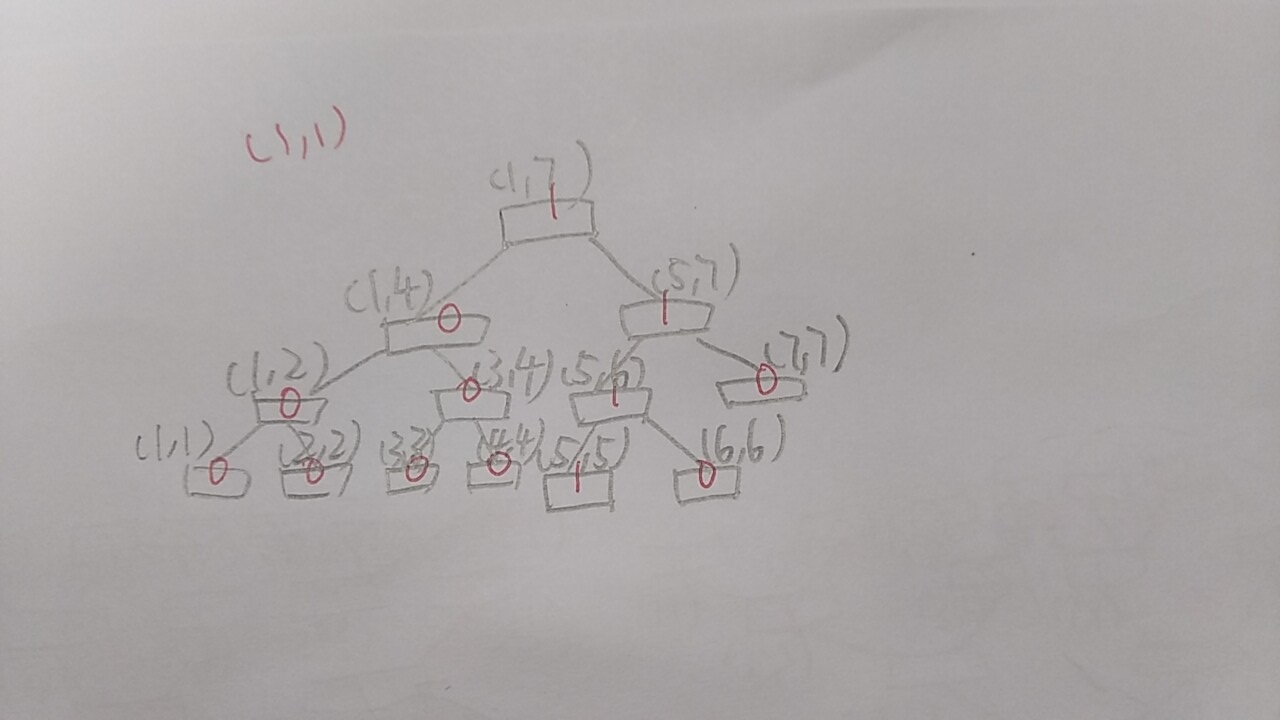
第二棵树我们发现只真正需要建的只有一条链,其他的可以由上一棵上里的结点代替:
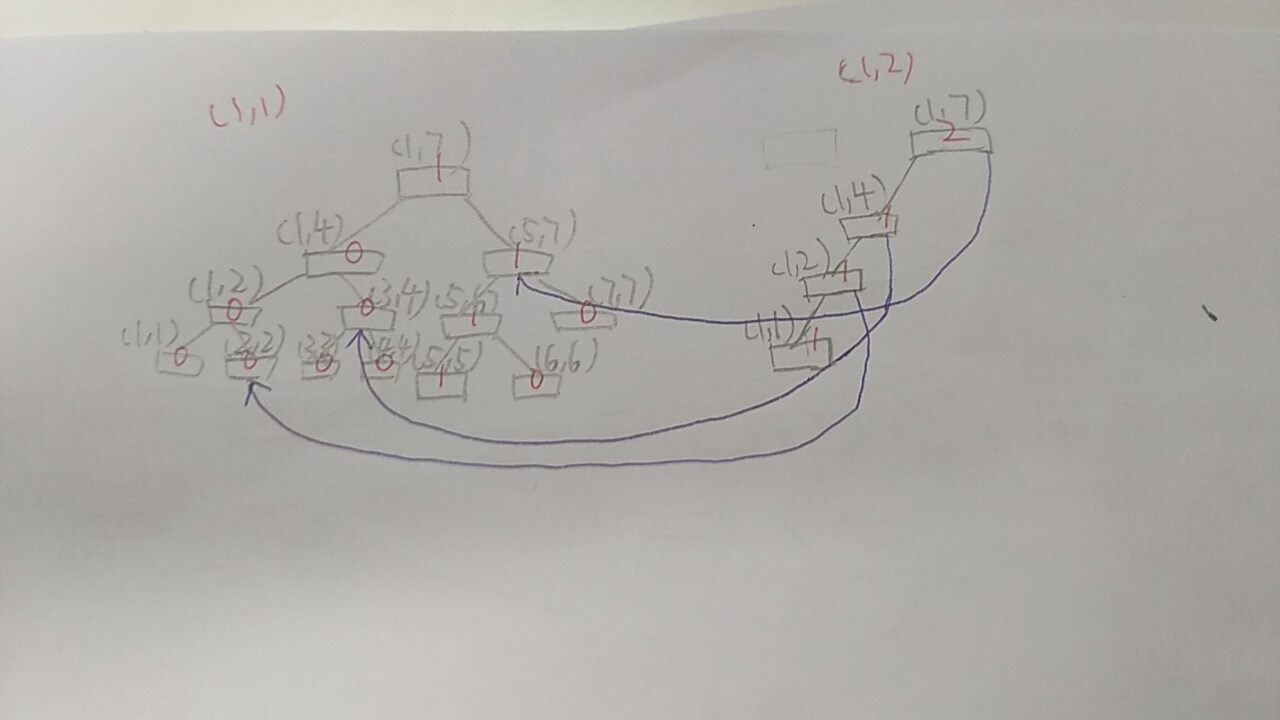
第三棵树由第二棵树插入a[3]=4得到:

这样的话分析下时间复杂度是O(N)建第一棵树加上(N-1)次插入,每次插入O(logN),所以总复杂度是O(N*logN);再分析空间复杂度是第一棵树2*N加上(N-1)*logN(每次加一条链子,不知道为什么我想到了蜡烛和皮鞭...),所以空间开20*MAXN就行了,也可以接受。
这样的话我们能logN处理(1,r)第k大的询问,那怎么处理(l,r)第k大的询问呢?
=====如果有按(l,r)建的权值线段树就好了====
===思考===思考===
我们可以通过(1,l-1)和(1,r)这两棵权值线段树得到(l,r)的权值线段树吗?
===思考===思考===
可以!
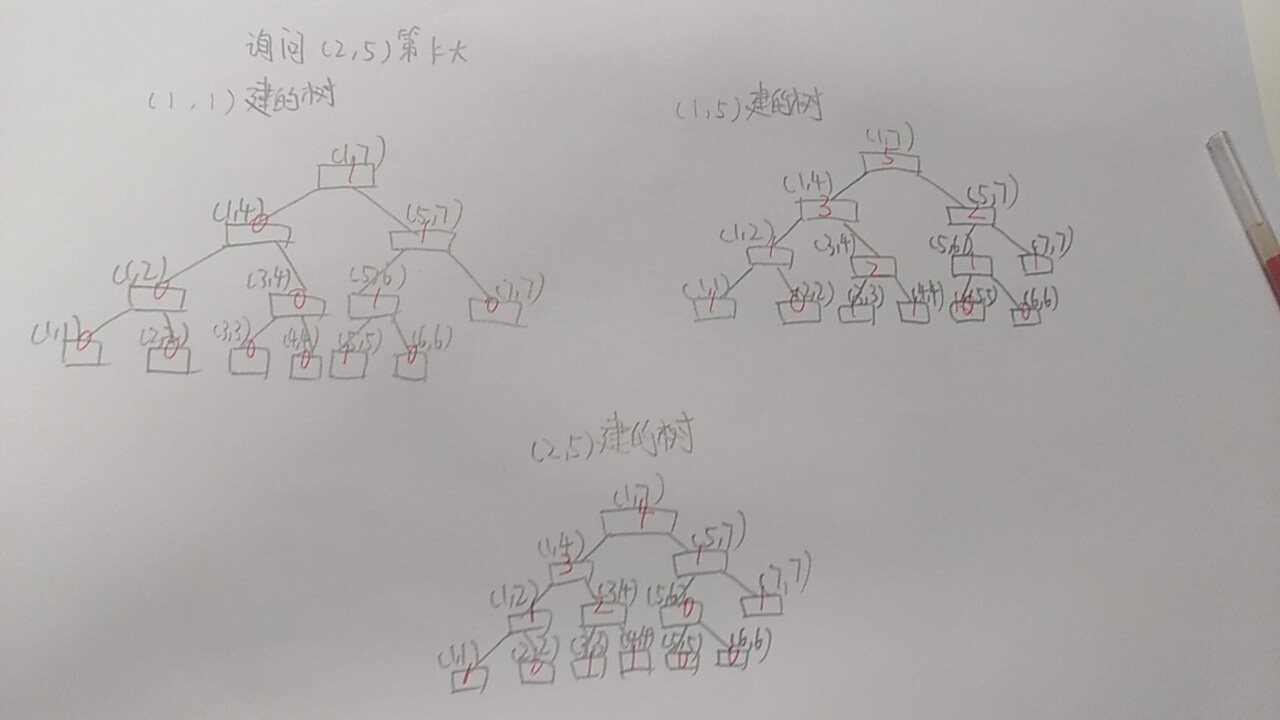
发现(2,5)线段树上每个结点的d值等于(1,5)树上对应结点d值减去(1,1)树上对应结点的d值,即V.d = Vr.d - Vl-1.d
因为对应结点意味着【值域区间】一样,那么(l,r)中特定值域区间内出现的数的次数就是(1,r)中数在当前值域下出现次数减去(1,l-1)中数在当前值域中出现次数。仔细想想很容易理解。【和前缀和思路类似,原理不一样。我们解答区间求和就是处理出前缀和,(l,r)区间的和就是sum[r]-sum[l-1] 】
那么就做完了!
以上是思路,具体实现可以看下面:
1 #include<iostream> 2 #include<algorithm> 3 #include<map> 4 #define MAXN 100000 5 using namespace std; 6 7 struct node{ 8 int l,r; 9 int d; 10 node *ls,*rs; 11 }pool[20*MAXN]; 12 13 int n,m,a[MAXN+5],b[MAXN+5]; 14 map<int,int> getRank,getValue; 15 node *root[MAXN+5]; 16 17 int top; 18 node* buildT(int l,int r){//root[0] 19 node* p = pool + (++top); 20 p->l=l; p->r=r; 21 if(l==r) return p; 22 int mid=(l+r)/2; 23 p->ls = buildT(l,mid); p->rs = buildT(mid+1,r); 24 return p; 25 } 26 27 node* update(node* rt,int rank){//基于线段树rt的update,在里面加入rank 28 int l=rt->l; int r=rt->r; 29 node* p = pool + (++top); 30 p->l = l; p->r = r; 31 p->d = rt->d + 1; //保证rank一定在rt的值域里 32 if(l==r) return p; 33 34 int mid=(l+r)/2; 35 if( rank>mid ) { 36 p->ls = rt->ls; 37 p->rs = update(rt->rs,rank); 38 return p; 39 } 40 else { 41 p->rs = rt->rs; 42 p->ls = update(rt->ls,rank); 43 return p; 44 } 45 } 46 47 int query(node* lt,node *rt,int k){//假设t是按(l,r)建立起的权值线段树的根 48 //lt和rt的值域区间一定是一样的 49 if(lt->l==lt->r) return lt->l; //这个时候k一定是1 50 int ld = rt->ls->d - lt->ls->d;//ld是t左子树值域区间里 能取得到的数的数量 51 52 if(k<=ld) return query(lt->ls,rt->ls,k);//第k大数的值 在左子树的值域里 53 return query(lt->rs,rt->rs,k-ld);//我们要找的第k大,就是右区间里的第k-ld大 54 } 55 56 int main(){ 57 cin>>n>>m; 58 for(int i=1;i<=n;i++) { cin>>a[i]; b[i]=a[i]; } 59 sort(b+1,b+1+n); 60 for(int i=1;i<=n;i++) { getRank[ b[i] ] = i; getValue[i] = b[i]; }//输入的每个数 different 61 62 //开始建树 63 root[0]=buildT(1,n);//值域范围是1-n 64 for(int i=1;i<=n;i++) root[i] = update( root[i-1],getRank[ a[i] ] ); 65 66 for(int i=1;i<=m;i++){ 67 int l,r,k; cin>>l>>r>>k; 68 cout<< getValue[ query( root[l-1],root[r],k ) ]<<endl; 69 } 70 71 72 return 0; 73 }
尼伯龙根里那个磅礴的雨夜,咆哮的父亲和狂奔的少年,还有炽烈燃烧的黄金瞳