给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例:
输入: [-2,1,-3,4,-1,2,1,-5,4]
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
进阶:
如果你已经实现复杂度为 O(n) 的解法,尝试使用更为精妙的分治法求解。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/maximum-subarray
方法一:暴力求解,时间复杂度O(n^2)
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int max = nums[0];
int i, j, k;
int sum;
int numsSize = nums.size();
for(i = 0; i < numsSize;i++) //子序列开始位置
{
sum = 0;
for(j = i; j < numsSize;j++) //子序列结束位置
{
sum += nums[k];
if(sum > max)
max = sum;
}
}
return max;
}
};
方法二:贪心算法,时间复杂度O(n)
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int max = nums[0];
int sum = 0;
for(int i = 0;i < nums.size(); i++)
{
sum += nums[i];
if(sum > max)
max = sum;
if(sum < 0) //如果和为负数,去掉前面序列的和便得到更优的解
sum = 0;
}
return max;
}
};
方法三:leetcode官方的动态规划方法
动态规划转移方程:
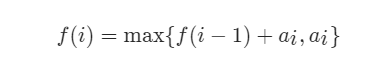
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int pre = 0, maxAns = nums[0];
for (const auto &x: nums) {
pre = max(pre + x, x);
maxAns = max(maxAns, pre);
}
return maxAns;
}
};