1.二叉树的最大深度
题目链接:https://leetcode-cn.com/problems/maximum-depth-of-binary-tree
题目描述:给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例:
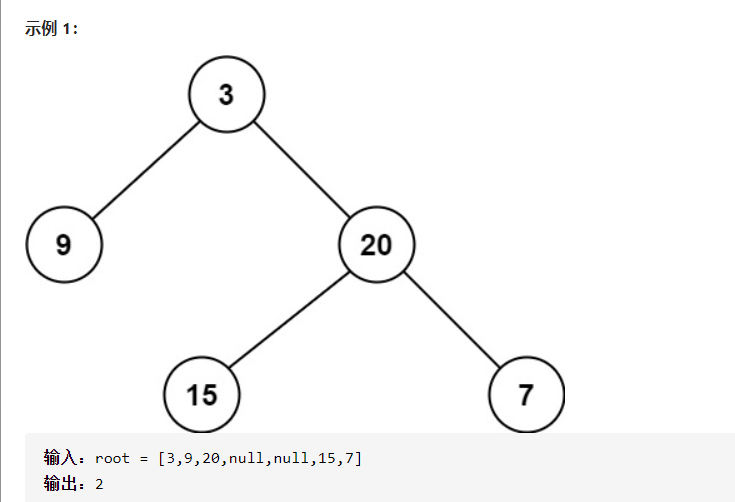
给定二叉树 [3,9,20,null,null,15,7],

返回它的最大深度 3 。
解题:当前节点树的高度 = max(当前节点左子树高度,当前节点右子树高度) + 1
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int getDepth(TreeNode* node)
{
if(node == nullptr)
{
return 0;
}else
{
int leftDepth = getDepth(node->left);
int rightDepth = getDepth(node->right);
int depth = 1 + max(leftDepth, rightDepth);
return depth;
}
}
int maxDepth(TreeNode* root) {
return getDepth(root);
}
};
2.N叉树的最大深度
题目链接:https://leetcode-cn.com/problems/maximum-depth-of-n-ary-tree
题目描述:
给定一个 N 叉树,找到其最大深度。
最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。N 叉树输入按层序遍历序列化表示,每组子节点由空值分隔(请参见示例)。
示例 1:
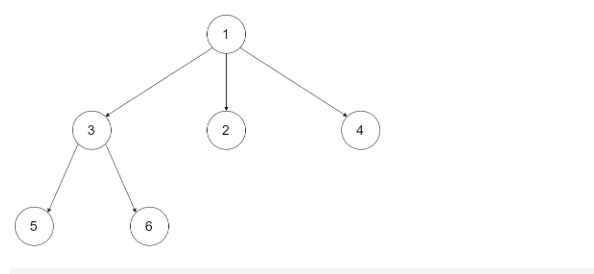
输入:root = [1,null,3,2,4,null,5,6]
输出:3
/*
// Definition for a Node.
class Node {
public:
int val;
vector<Node*> children;
Node() {}
Node(int _val) {
val = _val;
}
Node(int _val, vector<Node*> _children) {
val = _val;
children = _children;
}
};
*/
class Solution {
public:
int maxDepth(Node* root) {
int depth = 0;
if(root == NULL)
return 0;
for(auto iter: root->children)
{
int temp = maxDepth(iter);
depth = max(depth, temp);
}
return 1 + depth;
}
};
3.二叉树的最小深度
题目链接:https://leetcode-cn.com/problems/minimum-depth-of-binary-tree/
题目描述:
给定一个二叉树,找出其最小深度。最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明:叶子节点是指没有子节点的节点。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int getDepth(TreeNode* node)
{
if(node == nullptr)
return 0;
int leftDepth = getDepth(node->left);
int rightDepth = getDepth(node->right);
if(node->left == nullptr && node->right != nullptr) //左子树为空,最小高度由右子树决定
return 1 + rightDepth;
if(node->right == nullptr && node->left != nullptr) //右子树为空,最小高度由左子树决定
return 1 + leftDepth;
return 1 + min(leftDepth, rightDepth); //左右子树不为空,返回左右子树的最小高度
}
int minDepth(TreeNode* root) {
return getDepth(root);
}
};