（动态规划）cf 431C

C. k-Tree

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Quite recently a creative student Lesha had a lecture on trees. After the lecture Lesha was inspired and came up with the tree of his own which he called a k-tree.

A k-tree is an infinite rooted tree where:

• each vertex has exactly k children;
• each edge has some weight;
• if we look at the edges that goes from some vertex to its children (exactly k edges), then their weights will equal 1, 2, 3, ..., k.

The picture below shows a part of a 3-tree.

As soon as Dima, a good friend of Lesha, found out about the tree, he immediately wondered: "How many paths of total weight n (the sum of all weights of the edges in the path) are there, starting from the root of a k-tree and also containing at least one edge of weight at least d?".

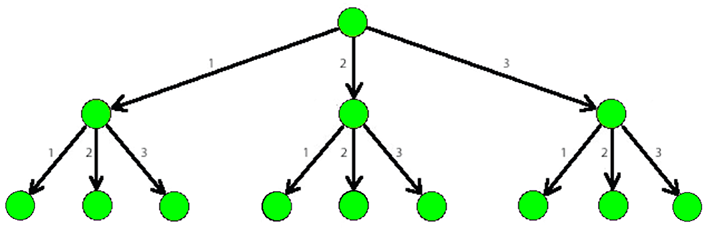
Help Dima find an answer to his question. As the number of ways can be rather large, print it modulo1000000007 (109 + 7).

Input

A single line contains three space-separated integers: n, k and d (1 ≤ n, k ≤ 100; 1 ≤ d ≤ k).

Output

Print a single integer — the answer to the problem modulo 1000000007 (109 + 7).

Sample test(s)

input

3 3 2

output

3

input

3 3 3

output

1

input

4 3 2

output

6

input

4 5 2

output

7

神奇的动态规划啊啊啊啊啊啊，

两个状态，dp[n][0,1]           0,1代表是否选超过d的。

dp[i+j][0]+=dp[i][0] j<d

dp[i+j][1]+=dp[i][0] j>=d

dp[i+j][1]+=dp[i][1]

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<string>
#include<algorithm>
using namespace std;
#define LL long long
#define MOD 1000000007
LL n,k,d,dp[110][2];
int main()
{
      scanf("%I64d%I64d%I64d",&n,&k,&d);
      memset(dp,0,sizeof(dp));
      dp[0][0]=1;
      for(int i=0;i<n;i++)
      {
            for(int j=1;j<=k;j++)
            {
                  if(i+j>n) continue;
                  if(j<d) dp[i+j][0]+=dp[i][0];
                  else dp[i+j][1]+=dp[i][0];
                  dp[i+j][1]+=dp[i][1];
                  dp[i+j][0]=dp[i+j][0]%MOD;
                  dp[i+j][1]=dp[i+j][1]%MOD;
            }
      }
      printf("%I64d",dp[n][1]);
      return 0;
}