数据结构与算法-复杂度

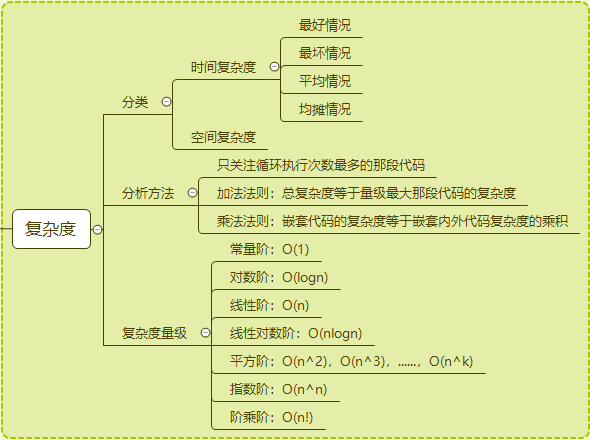
　　数据结构和算法本身解决的是，如何让代码运行得更快，如何让代码更省存储空间。所以就分为两个维度分析，时间复杂度、空间复杂度。复杂度分析能事先初略的估计算法的执行效率。

时间复杂度

　　大O复杂度表示法

　　大O符号是由德国数论学家保罗·巴赫曼（Paul Bachmann）在其1892年的著作《解析数论》（Analytische Zahlentheorie）首先引入的。而这个记号则是在另一位德国数论学家艾德蒙·朗道（Edmund Landau）的著作中才推广的，因此它有时又称为朗道符号（Landau symbol）。代表“order of ...”（……阶）的大O，最初是一个大写的希腊字母'Ο'（Omicron），现今用的是英文大写字母'O'，但从来不是阿拉伯数字'0'。--摘百度百科

　　T(n)=O(F(n)) ：T(n)代表代码执行时间，F(n)代表代码总执行次数，O表示代码执行时间与代码总执行次数成正比

　　复杂度量级：

　　O(1):

　　O(1)是一种常量阶表示法：最低的时间复杂度，如执行了一行声明或预算的一行代码，示例：　　

int x = 1;
int y = 10;
int z = x + y;

　　O(logn)、O(nlogn)

　　对数阶表示法：当数据增大n倍时，耗时增大logn倍，以下代码以2为底示例：

inti=1; 
while (i <= n) {
 i = i * 2; 
}

　　i的值从1开始，没循环一次就乘以2，当i大于等于n时，循环结束。时间复杂度是O(log2n)

　　O(n)

　　线性阶表示法：n越大、耗时越长，比如遍历

for(int i = 0; i < n; i++){    
    ...
}

　　O(n^2)，O(n^3)，......，O(n^k)

　　平方阶表示法：数据量增大n倍时，耗时增大n的平方倍，比如冒泡、选择、插入排序

for(...){
  for(...){
      ...
  }  
}

　　O(2^n)、O(n!)

　　指数阶表示法：随着数据规模n增大，对应算法的时间复杂度成2^n次方级变化，比如斐波那契数列

public int Fibonacci(int number)
{
    if (number <= 1) return number;

    return Fibonacci(number - 2) + Fibonacci(number - 1);
}

　　小结：

　　从低阶到高阶

　　O(1) < O(logn) < O(nlogn) < O(n) < O(n^2) < O(2^n) < O(n!) < O(n^n)

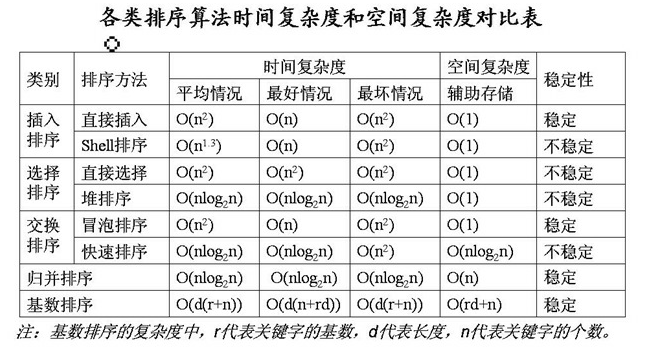
空间复杂度

　　空间复杂度的衡量取决于程序运行时占用内存空间的大小，当内存空间比较受限的时候，可以考虑时间换空间。时间复杂度和空间复杂度往往是相互影响的，有时为空提升执行效率，往往会牺牲存储空间，比如程序的缓存。

总结：