这个是昨天下午的cf div2 D题
当时没搞明白怎么做 想了一个三分t时间的选择的vx,可以求出vy,这样t时间时的到达坐标可以求出来 就可以求出来从该坐标到终点还需要的时间t2 t+t2就是答案
但是写的时候遇到了一个很大的问题 就是向量的方向问题
可以求出来vx 但是vy用sqrt(vmax*vmax-vx*vx)时 有两个方向
而且vx本身也有两个方向 和路径x同向或者反向
所以写起来特别麻烦 今天搞到一半又放弃了
后来仔细想了下 如果我们把航行和风速分开考虑
t时间内航行到的点是以fx fy为圆心 t*vmax为半径的圆上的点
而t时间内风速的作用 使得这个圆整体向 vx*t vy*t移动
所以可以求出来t时间时的所有可以到达的点 它是一个平移之后的圆
如果终点在这个圆内,则时间t内可以到达
否则就得在时间t之后到达
时间t后
风速对终点的影响 相当于把终点往 -wx*t,-wy*t移动
二分一下答案求起点终点距离等于两半径之和的时间 就是答案
#include<bits/stdc++.h>
using namespace std;
int fx,fy,tx,ty;
double vmax;
double t;
double vx,vy,wx,wy;
double xx1,yy1,xx2,yy2;
double rr1,rr2;
double sqr(double k)
{
return k*k;
}
double dis(double fx,double fy,double tx,double ty)
{
return sqrt(sqr(tx-fx)+sqr(ty-fy));
}
void bs1()
{
double l=1e-11,r=t,mid,ans;
ans=0;
while(r>=l+1e-9)
{
mid=(l+r)/2;
xx1=fx+vx*mid;
yy1=fy+vy*mid;
rr1=vmax*mid;
//cout<<"t="<<t<<endl;
//cout<<"xx1="<<xx1<<" yy1="<<yy1<<" rr1="<<rr1<<endl;
if(dis(xx1,yy1,xx2,yy2)<=rr1)
{
ans=mid;
r=mid;
}
else
l=mid;
}
printf("%.17lf
",ans);
}
void bs2()
{
double l=1e-11,r=1e11,mid,ans;
ans=0;
while(r>=l+1e-9)
{
mid=(l+r)/2;
xx2=tx-wx*mid;
yy2=ty-wy*mid;
rr2=vmax*mid;
if(dis(xx1,yy1,xx2,yy2)<=rr1+rr2)
{
ans=mid;
r=mid;
}
else
l=mid;
}
printf("%.17lf
",ans+t);
}
int main()
{
cin>>fx>>fy>>tx>>ty>>vmax>>t>>vx>>vy>>wx>>wy;
xx1=fx+vx*t;
yy1=fy+vy*t;
rr1=vmax*t;
xx2=tx;
yy2=ty;
//cout<<xx1<<" "<<yy1<<" "<<rr1<<endl;
if(dis(xx1,yy1,xx2,yy2)<=rr1)
bs1();
else
bs2();
return 0;
}
 meters per second.
meters per second. seconds the new position of the dirigible will be
seconds the new position of the dirigible will be 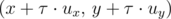 .
.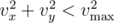 and
and 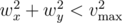 .
. .
.