[CF1486F] Pairs of Paths

Problem

给定一棵树和若干个点对 ((u,v)) 给出的树上最短路径，求满足 路径交仅有一个点 的 无序 路径对（即 ((a,b)) 和 ((b,a)) 算一次）。

Sol & Code

交仅为一个点只有两种情况：两条路径 LCA 在同一个点或不在同一个点。

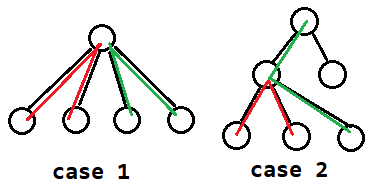
分别计算。第一种使用容斥：交一个点、两个点、三个点加加减减；第二种较为简单，无需考虑交三个点的情况。注意要去掉两种情况之间的影响。复杂度 (mathcal O(nlog n))。

#include <bits/stdc++.h>
using std::vector; using std::swap;
typedef long long LL;
const int N = 300005;
int n, m;
struct Edge { int v, nxt; } e[N * 2];
int G[N * 2], edges = 0;
void adde(int u, int v) {
	e[edges++] = (Edge){v, G[u]}; G[u] = edges - 1;
}
int fa[19][N], dep[N];
void dfs(int u, int f) {
	dep[u] = dep[f] + 1; fa[0][u] = f;
	for (int i = 1; i < 19; i++) fa[i][u] = fa[i - 1][fa[i - 1][u]];
	for (int i = G[u]; ~i; i = e[i].nxt)
		if (e[i].v != f) dfs(e[i].v, u);
}
void get(int &u, int d) {
	for (int i = 0; d; i++, d >>= 1)
		if (d & 1) u = fa[i][u];
}
int lca(int x, int y) {
	if (dep[x] < dep[y]) swap(x, y);
	get(x, dep[x] - dep[y]);
	if (x == y) return x;
	for (int i = 18; ~i; i--)
		if (fa[i][x] != fa[i][y]) x = fa[i][x], y = fa[i][y];
	return fa[0][x];
}
int sum[N], c[N]; LL ans = 0;
struct node {
	int x, y;
	bool operator < (const node &o) const {
		return x != o.x ? x < o.x : y < o.y;
	}
};
vector<node> tg[N];
void Dfs(int u) {
	for (int i = G[u], v; ~i; i = e[i].nxt) 
		if (v = e[i].v, v != fa[0][u])
			Dfs(v), sum[u] += sum[v];
	c[u] = sum[u] - tg[u].size();
	sort(tg[u].begin(), tg[u].end());
	ans += 1LL * tg[u].size() * c[u];
	for (int i = 0; i < tg[u].size(); i++) {
		if (tg[u][i].x) c[tg[u][i].x]--;
		if (tg[u][i].y) c[tg[u][i].y]--;
	}
	for (int i = 0; i < tg[u].size(); i++) {
		if (tg[u][i].x) ans -= c[tg[u][i].x];
		if (tg[u][i].y) ans -= c[tg[u][i].y];
	}
	LL tot = 0;
	for (int i = G[u], v; ~i; i = e[i].nxt)
		if (v = e[i].v, v != fa[0][u]) c[v] = 0;
	for (int i = 0; i < tg[u].size(); i++) {
		if (tg[u][i].x) c[tg[u][i].x]++;
		if (tg[u][i].y) c[tg[u][i].y]++;
	}
	tot += 1LL * tg[u].size() * tg[u].size();
	for (int l = 0, r = 0; l < tg[u].size(); l = r) {
		while (r < tg[u].size() && tg[u][l].x == tg[u][r].x && tg[u][l].y == tg[u][r].y) r++;
		if (tg[u][l].x) tot -= 1LL * (r - l) * c[tg[u][l].x];
		if (tg[u][l].y) tot -= 1LL * (r - l) * c[tg[u][l].y];
		if (!tg[u][l].x || !tg[u][l].y) continue;
		tot += 1LL * (r - l) * (r - l);
	}
	for (int i = 0; i < tg[u].size(); i++) {
		if (tg[u][i].x || tg[u][i].y) break;
		tot--;
	}
	ans += tot / 2;
}
int main() {
	scanf("%d", &n);
	memset(G, -1, sizeof G);
	for (int i = 1; i < n; i++) {
		int u, v; scanf("%d%d", &u, &v);
		adde(u, v), adde(v, u);
	}
	dfs(1, 0);
	scanf("%d", &m);
	for (int i = 1; i <= m; i++) {
		int u, v, t, x, y; scanf("%d%d", &u, &v); t = lca(u, v);
		if (u == t) x = 0; else x = u, get(x, dep[u] - dep[t] - 1);
		if (v == t) y = 0; else y = v, get(y, dep[v] - dep[t] - 1);
		if (x > y) swap(x, y);
		tg[t].push_back((node){x, y});
		sum[u]++, sum[v]++, sum[t]--, sum[fa[0][t]]--;
	}
	Dfs(1);
	printf("%lld", ans);
	return 0;
}