旋转卡壳算法

 旋转卡壳可以用于求凸包的直径、宽度，两个不相交凸包间的最大距离和最小距离等。虽然算法的思想不难理解，但是实现起来真的很容易让人“卡壳”。
   拿凸包直径(也就是凸包上最远的两点的距离）为例，原始的算法是这样子：
  
      

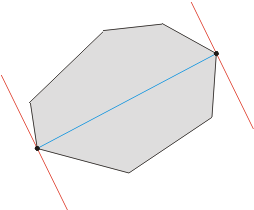
1. Compute the polygon's extreme points in the y direction. Call them ymin and ymax.
2. Construct two horizontal lines of support through ymin and ymax. Since this is already an anti-podal pair, compute the distance, and keep as maximum.
3. Rotate the lines until one is flush with an edge of the polygon.
4. A new anti-podal pair is determined. Compute the new distance, compare to old maximum, and update if necessary.
5. Repeat steps 3 and 4 until the anti-podal pair considered is (ymin,ymax) again.
6. Output the pair(s) determining the maximum as the diameter pair(s).

   更具体的可参见http://cgm.cs.mcgill.ca/~orm/rotcal.frame.html
      

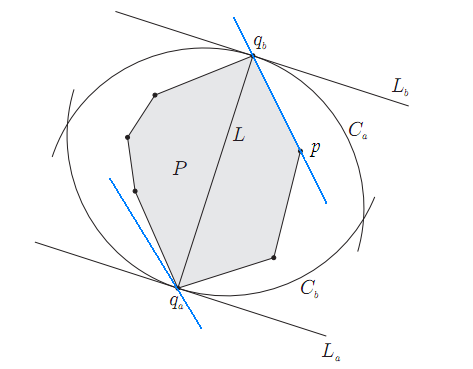
   直接按照这个描述可以实现旋转卡壳算法，但是代码肯定相当冗长。逆向思考，如果q_a，q_b是凸包上最远两点，必然可以分别过q_a，q_b画出一对平行线。通过旋转这对平行线，我们可以让它和凸包上的一条边重合,如图中蓝色直线，可以注意到，q_a是凸包上离p和q_b所在直线最远的点。于是我们的思路就是枚举凸包上的所有边，对每一条边找出凸包上离该边最远的顶点，计算这个顶点到该边两个端点的距离，并记录最大的值。直观上这是一个O(n²)的算法，和直接枚举任意两个顶点一样了。但是注意到当我们逆时针枚举边的时候，最远点的变化也是逆时针的，这样就可以不用从头计算最远点，而可以紧接着上一次的最远点继续计算(详细的证明可以参见上面链接中的论文)。于是我们得到了O(n)的算法。

//计算凸包直径，输入凸包ch，顶点个数为n，按逆时针排列，输出直径的平方
int rotating_calipers(Point *ch,int n)
{
    int q=1,ans=0;
    ch[n]=ch[0];
    for(int p=0;p<n;p++)
    {
        while(cross(ch[p+1],ch[q+1],ch[p])>cross(ch[p+1],ch[q],ch[p]))
            q=(q+1)%n;
        ans=max(ans,max(dist2(ch[p],ch[q]),dist2(ch[p+1],ch[q+1])));            
    }
    return ans; 
}

   很难想象这个看起来那么麻烦的算法只有这么几行代码吧！其中cross函数是计算叉积，可以想成是计算三角形面积，因为凸包上距离一条边最远 的点和这条边的两个端点构成的三角形面积是最大的。之所以既要更新(ch[p],ch[q])又要更新(ch[p+1],ch[q+1])是为了处理凸包 上两条边平行的特殊情况。

   poj2187要求的是平面点集上的最远点对，实际上就是该点集的凸包的直径。可能该题数据求得的凸包顶点数都不多，所以旋转卡壳算法相比普通的枚举算法并没有明显的优势。完整代码如下。

#include <cmath>
#include <algorithm>
#include <iostream>
using namespace std;
#define MAXN 50005

struct Point
{
    int x, y;
    bool operator < (const Point& _P) const
    {
        return y<_P.y||(y==_P.y&&x<_P.x);
    };
}pset[MAXN],ch[MAXN];

void convex_hull(Point *p,Point *ch,int n,int &len)
{
    sort(p, p+n);
    ch[0]=p[0];
    ch[1]=p[1];
    int top=1;
    for(int i=2;i<n;i++)
    {
        while(top>0&&cross(ch[top],p[i],ch[top-1])<=0)
            top--;
        ch[++top]=p[i];
    }
    int tmp=top;
    for(int i=n-2;i>=0;i--)
    {
        while(top>tmp&&cross(ch[top],p[i],ch[top-1])<=0)
            top--;
        ch[++top]=p[i];
    }
    len=top;    
}

int cross(Point a,Point b,Point o)      
{
    return (a.x - o.x) * (b.y - o.y) - (b.x - o.x) * (a.y - o.y);
}

int dist2(Point a,Point b)
{
    return (a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y);
}

int rotating_calipers(Point *ch,int n)
{
    int q=1,ans=0;
    ch[n]=ch[0];
    for(int p=0;p<n;p++)
    {
        while(cross(ch[p+1],ch[q+1],ch[p])>cross(ch[p+1],ch[q],ch[p]))
            q=(q+1)%n;
        ans=max(ans,max(dist2(ch[p],ch[q]),dist2(ch[p+1],ch[q+1])));            
    }
    return ans; 
}

int main()
{
    //freopen("in.txt","r",stdin);
    int n, len;
    while(scanf("%d", &n)!=EOF)
    {
        for(int i = 0;i < n;i++)
        {
            scanf("%d %d",&pset[i].x,&pset[i].y);
        }
        convex_hull(pset,ch,n,len);
        printf("%d\n",rotating_calipers(ch,len));
    }
    return 0;
}

   poj3608 要 求的是两个凸包的最近距离。这比求凸包直径麻烦了许多。我的基本思想还是分别枚举两个凸包的边，但是有些细节没能完全证明是正确的。虽然AC了，但目前这 还只是一个看起来正确的算法。这题的中间过程还需要计算点到线段的距离和两条平行线段的距离，比起2187麻烦了许多。

#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
#define MAXN 50000
#define EPS 1e-9
struct Point
{
    double x,y;
    Point (){}
    Point (double _x,double _y){x=_x;y=_y;}
}pm[MAXN],pn[MAXN];

double cross(Point a,Point b,Point o)
{
    return (o.x-a.x)*(o.y-b.y)-(o.x-b.x)*(o.y-a.y);
}

double dist(Point a,Point b)
{
    return (a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y);
}

double dot(Point a,Point b)
{
    return a.x*b.x+a.y*b.y;
}

void anticolockwise(Point *ch,int len)
{
    for(int i=0;i<len-2;i++)
    {
        double tmp=cross(ch[i],ch[i+1],ch[i+2]);
        if(tmp>EPS)
            return;
        else if(tmp<-EPS)
        {
            reverse(ch,ch+len);
            return;
        }
    }
}

double dis_point_to_seg(Point c,Point a,Point b)
{
    Point ab=Point(b.x-a.x,b.y-a.y);
    Point ac=Point(c.x-a.x,c.y-a.y);
    double f=dot(ab,ac);
    if(f<0) return dist(a,c);
    double D=dot(ab,ab);
    if(f>D) return dist(b,c);
    f=f/D;
    Point d=Point(a.x+f*ab.x,a.y+f*ab.y);
    return dist(d,c);
}

double dis_pall_seg(Point p1, Point p2, Point p3, Point p4)
{
    return min(min(dis_point_to_seg(p1, p3, p4), dis_point_to_seg(p2, p3, p4)),
     min(dis_point_to_seg(p3, p1, p2), dis_point_to_seg(p4, p1, p2)));
}

double rc(Point *ch1,Point *ch2,int n,int m)
{
    int q=0;
    int p=0;
    for(int i=0;i<n;i++) 
        if(ch1[i].y-ch1[p].y<-EPS)
            p=i;
    for(int i=0;i<m;i++)
        if(ch2[i].y-ch2[q].y>EPS)
            q=i;
    ch1[n]=ch1[0];
    ch2[m]=ch2[0];
    double tmp,ans=1e99;
    for(int i=0;i<n;i++)
    {
        while((tmp=cross( ch1[p+1],ch2[q+1],ch1[p]) - cross(ch1[p+1],ch2[q],ch1[p]) )>EPS)
            q=(q+1)%m;
        if(tmp<-EPS)
            ans=min(ans,dis_point_to_seg(ch2[q],ch1[p],ch1[p+1]));
        else
            ans=min(ans,dis_pall_seg(ch1[p],ch1[p+1],ch2[q],ch2[q+1]));
        p=(p+1)%n;
    }
    return ans;
            
}

int main()
{
    //freopen("in.txt","r",stdin);
    int n,m;
    while(scanf("%d %d",&n,&m))
    {
        if(n==0&&m==0)
            break;
        for(int i=0;i<n;i++)
            scanf("%lf %lf",&pn[i].x,&pn[i].y);
        for(int i=0;i<m;i++)
            scanf("%lf %lf",&pm[i].x,&pm[i].y);
        anticolockwise(pn,n);
        anticolockwise(pm,m);
        printf("%.5f\n",sqrt(min(rc(pn,pm,n,m),rc(pm,pn,m,n))));
    }
    return 0;
}